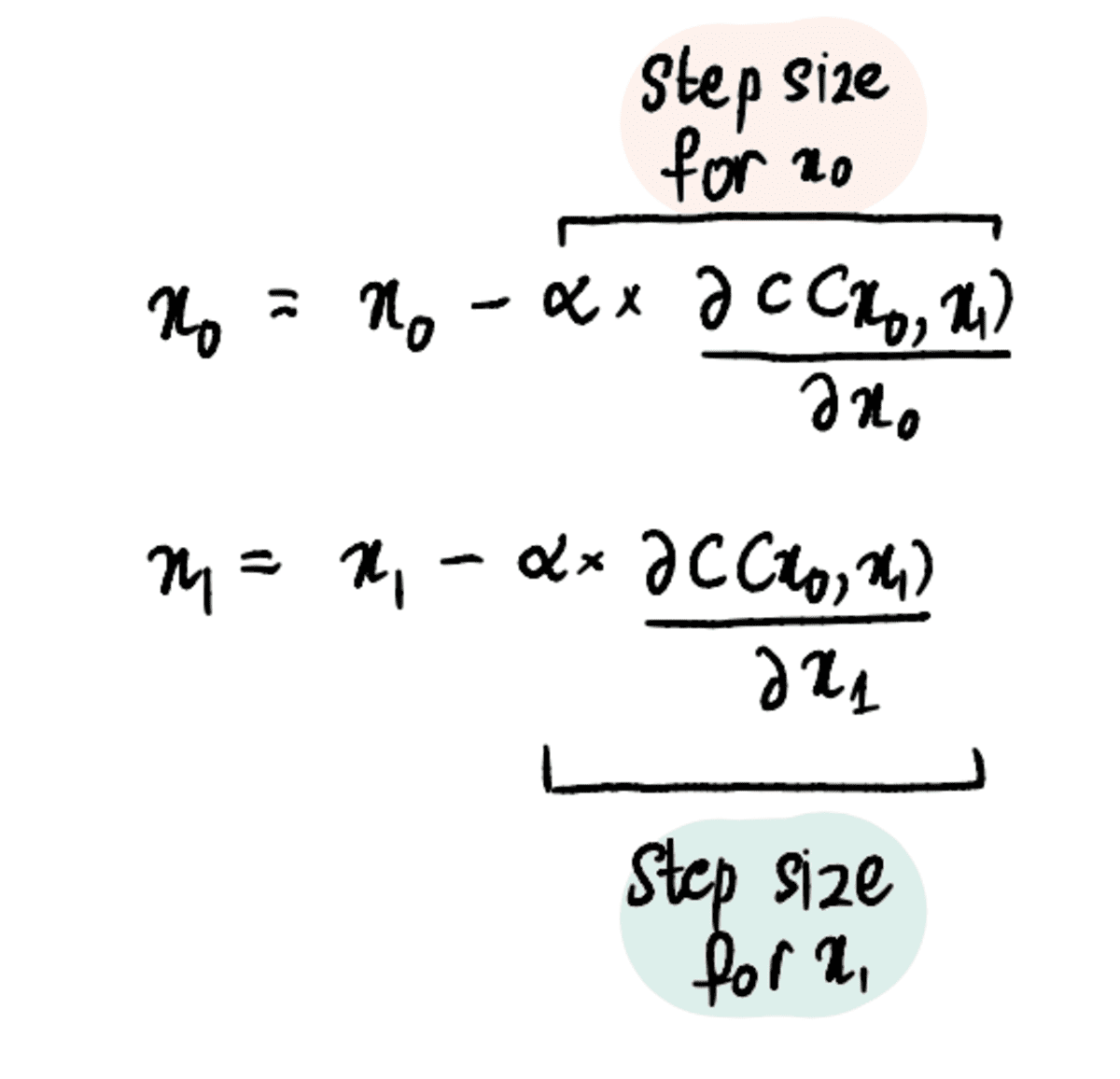বেসিকগুলিতে ফিরে যান, পার্ট ডস: গ্রেডিয়েন্ট ডিসেন্ট

আমাদের দ্বিতীয় পর্বে স্বাগতম প্রাথমিক স্তরে ফিরে আসা সিরিজ মধ্যে অগ্রভাগ, আমরা লিনিয়ার রিগ্রেশন এবং কস্ট ফাংশন ব্যবহার করে আমাদের বাড়ির দামের ডেটার জন্য সেরা-ফিটিং লাইন খুঁজে বের করার জন্য কভার করেছি। যাইহোক, আমরা সেই একাধিক পরীক্ষাও দেখেছি পথিমধ্যে রোধ করা মান ক্লান্তিকর এবং অদক্ষ হতে পারে. এই দ্বিতীয় অংশে, আমরা গ্রেডিয়েন্ট ডিসেন্টের আরও গভীরে অনুসন্ধান করব, একটি শক্তিশালী কৌশল যা আমাদের নিখুঁত খুঁজে পেতে সাহায্য করতে পারে পথিমধ্যে রোধ করা এবং আমাদের মডেল অপ্টিমাইজ করুন। আমরা এর পিছনের গণিতটি অন্বেষণ করব এবং এটি কীভাবে আমাদের লিনিয়ার রিগ্রেশন সমস্যায় প্রয়োগ করা যেতে পারে তা দেখব।

গ্রেডিয়েন্ট ডিসেন্ট হল একটি শক্তিশালী অপ্টিমাইজেশান অ্যালগরিদম দ্রুত এবং দক্ষতার সাথে একটি বক্ররেখার সর্বনিম্ন বিন্দু খুঁজে বের করার লক্ষ্য। এই প্রক্রিয়াটি কল্পনা করার সর্বোত্তম উপায় হল কল্পনা করা যে আপনি একটি পাহাড়ের চূড়ায় দাঁড়িয়ে আছেন, সোনায় ভরা ধনভান্ডারের সাথে উপত্যকায় আপনার জন্য অপেক্ষা করছে।

 

 

যাইহোক, উপত্যকার সঠিক অবস্থান অজানা কারণ এটি অত্যন্ত অন্ধকার এবং আপনি কিছুই দেখতে পাচ্ছেন না। তদুপরি, আপনি অন্য কেউ করার আগেই উপত্যকায় পৌঁছাতে চান (কারণ আপনি নিজের জন্য সমস্ত ধন চান)। গ্রেডিয়েন্ট ডিসেন্ট আপনাকে ভূখণ্ডে নেভিগেট করতে এবং এটিতে পৌঁছাতে সহায়তা করে অনুকূল বিন্দু দক্ষতার সাথে এবং দ্রুত. প্রতিটি পয়েন্টে এটি আপনাকে বলবে যে কতগুলি পদক্ষেপ নিতে হবে এবং সেগুলি আপনাকে কোন দিকে নিতে হবে৷

একইভাবে, অ্যালগরিদম দ্বারা নির্ধারিত পদক্ষেপগুলি ব্যবহার করে আমাদের লিনিয়ার রিগ্রেশন সমস্যায় গ্রেডিয়েন্ট ডিসেন্ট প্রয়োগ করা যেতে পারে। ন্যূনতম খুঁজে বের করার প্রক্রিয়াটি কল্পনা করতে, এর প্লট করা যাক MSE বক্ররেখা আমরা ইতিমধ্যে জানি যে বক্ররেখার সমীকরণ হল:

 

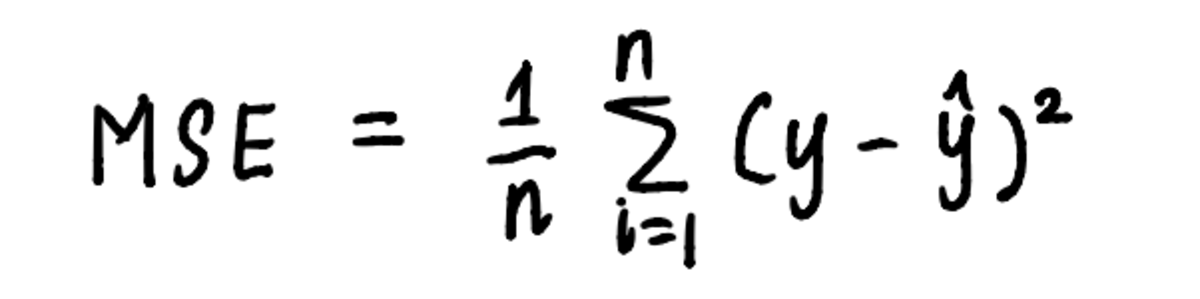
বক্ররেখার সমীকরণ হল MSE গণনা করতে ব্যবহৃত সমীকরণ

 

এবং থেকে আগের প্রবন্ধে, আমরা জানি যে সমীকরণ MSE আমাদের সমস্যা হল:

 

 

আমরা জুম আউট করলে আমরা দেখতে পাব যে একটি MSE বক্ররেখা (যা আমাদের উপত্যকার অনুরূপ) একগুচ্ছ প্রতিস্থাপন করে পাওয়া যেতে পারে পথিমধ্যে রোধ করা উপরের সমীকরণে মান। তাই এর 10,000 মান প্লাগ করা যাক পথিমধ্যে রোধ করা, এই মত দেখায় একটি বক্ররেখা পেতে:

 

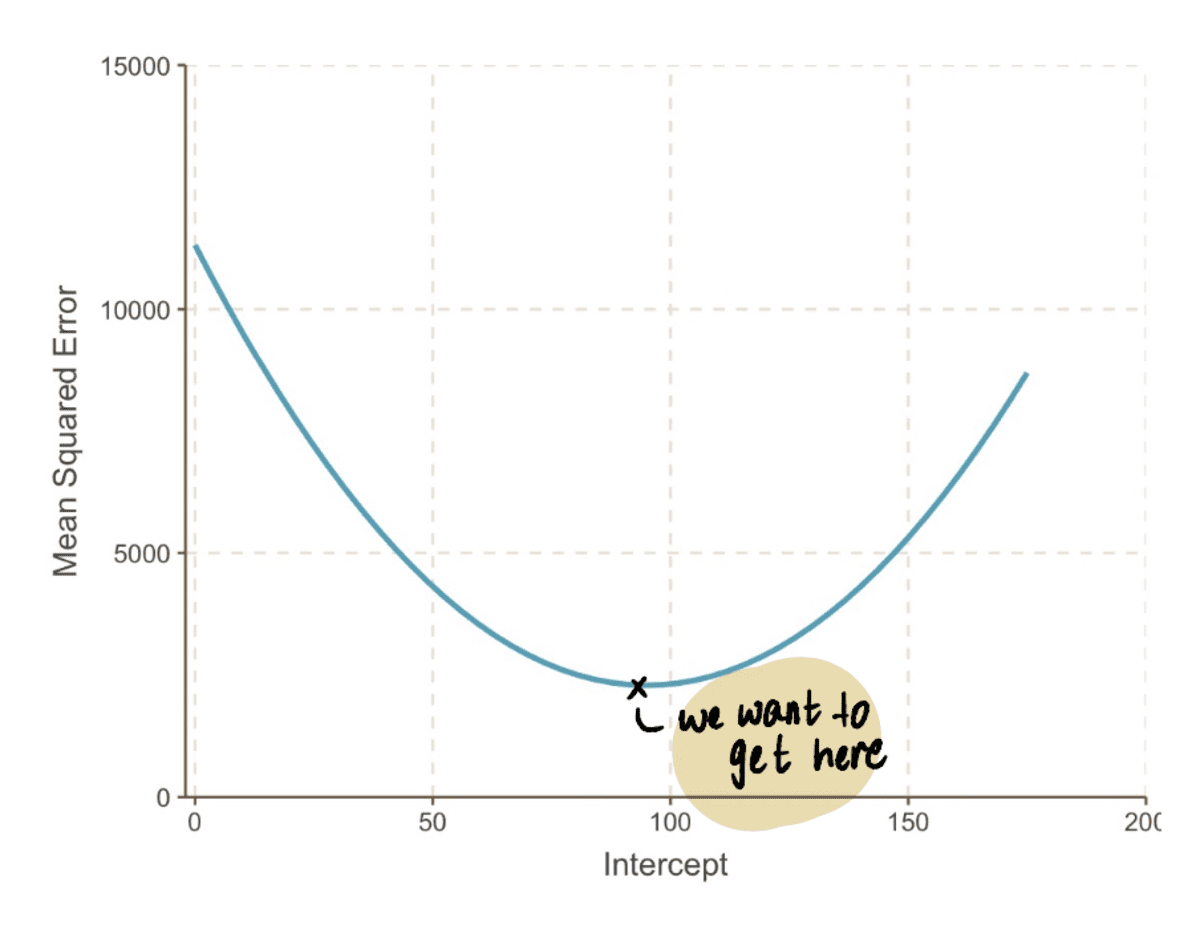
বাস্তবে, MSE বক্ররেখা কেমন তা আমরা জানি না

 

এর তলানিতে পৌঁছানোই লক্ষ্য MSE বক্ররেখা, যা আমরা এই পদক্ষেপগুলি অনুসরণ করে করতে পারি:

ধাপ 1: ইন্টারসেপ্ট মানের জন্য একটি এলোমেলো প্রাথমিক অনুমান দিয়ে শুরু করুন

এই ক্ষেত্রে, এর জন্য আমাদের প্রাথমিক অনুমান অনুমান করা যাক পথিমধ্যে রোধ করা মান হল 0।

ধাপ 2: এই সময়ে MSE বক্ররেখার গ্রেডিয়েন্ট গণনা করুন

সার্জারির  নতিমাত্রা একটি বিন্দুতে একটি বক্ররেখাটি স্পর্শক রেখা দ্বারা প্রতিনিধিত্ব করা হয় (একটি অভিনব উপায় যে রেখাটি কেবলমাত্র সেই বিন্দুতে বক্ররেখা স্পর্শ করে)। উদাহরণস্বরূপ, পয়েন্ট A এ, নতিমাত্রা এর MSE বক্ররেখা লাল স্পর্শক রেখা দ্বারা উপস্থাপিত হতে পারে, যখন বাধা 0 এর সমান হয়।

 

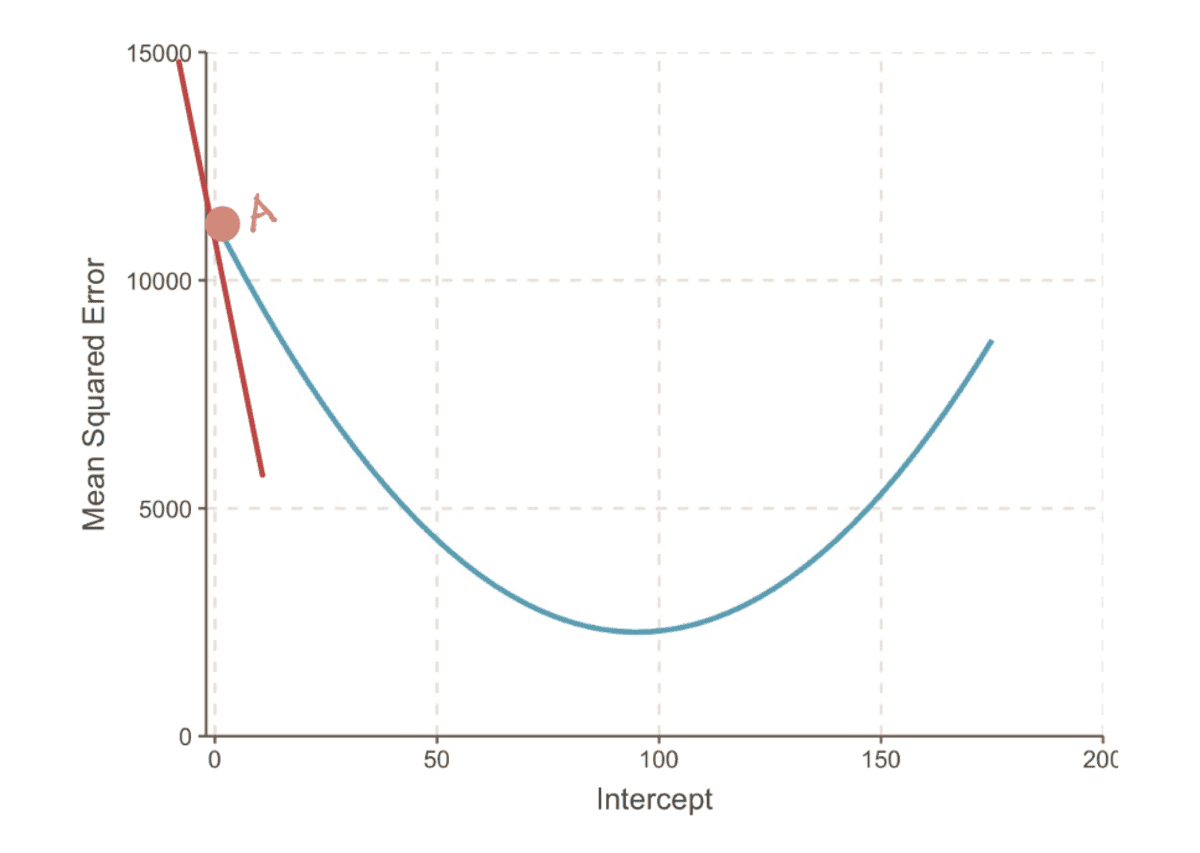
MSE বক্ররেখার গ্রেডিয়েন্ট যখন ইন্টারসেপ্ট = 0

 

এর মান নির্ধারণ করার জন্য নতিমাত্রা, আমরা ক্যালকুলাস সম্পর্কে আমাদের জ্ঞান প্রয়োগ করি। বিশেষ করে, দ নতিমাত্রা সাপেক্ষে বক্ররেখার ডেরিভেটিভের সমান পথিমধ্যে রোধ করা একটি নির্দিষ্ট সময়ে। এটি হিসাবে চিহ্নিত করা হয়:

 

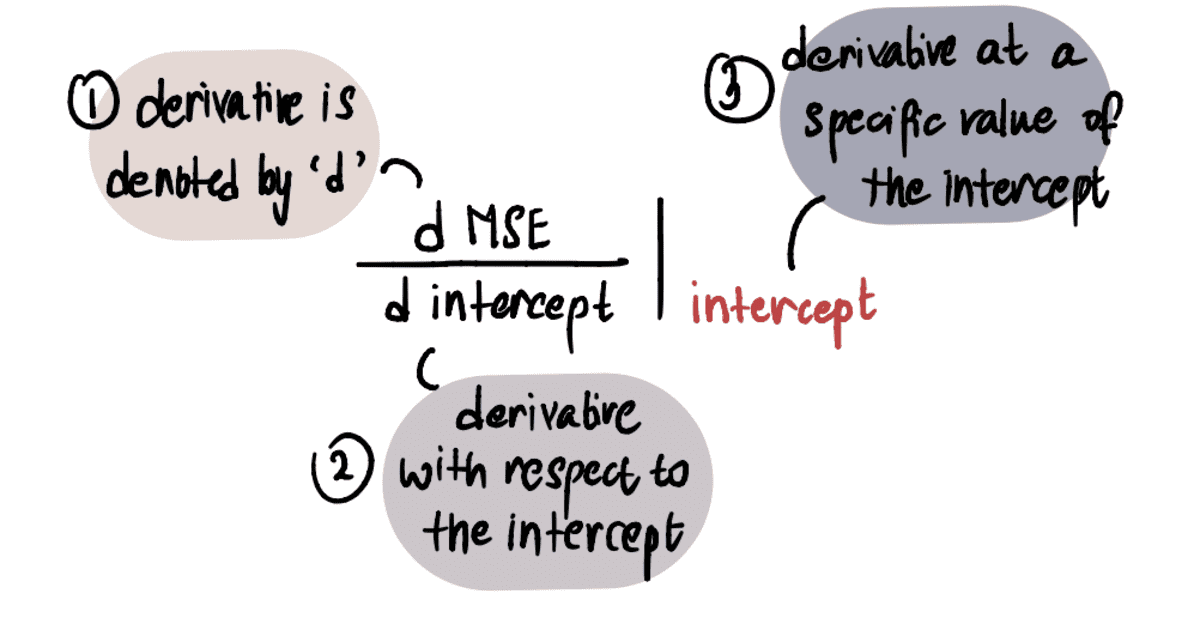
দ্রষ্টব্য: আপনি যদি ডেরিভেটিভের সাথে অপরিচিত হন তবে আমি এটি দেখার পরামর্শ দিই খান একাডেমির ভিডিও যদি আগ্রহী হন. অন্যথায় আপনি পরবর্তী অংশটি দেখতে পারেন এবং এখনও নিবন্ধের বাকি অংশটি অনুসরণ করতে সক্ষম হবেন।

আমরা গণনা MSE বক্ররেখার ডেরিভেটিভ নিম্নরূপ:

 

 

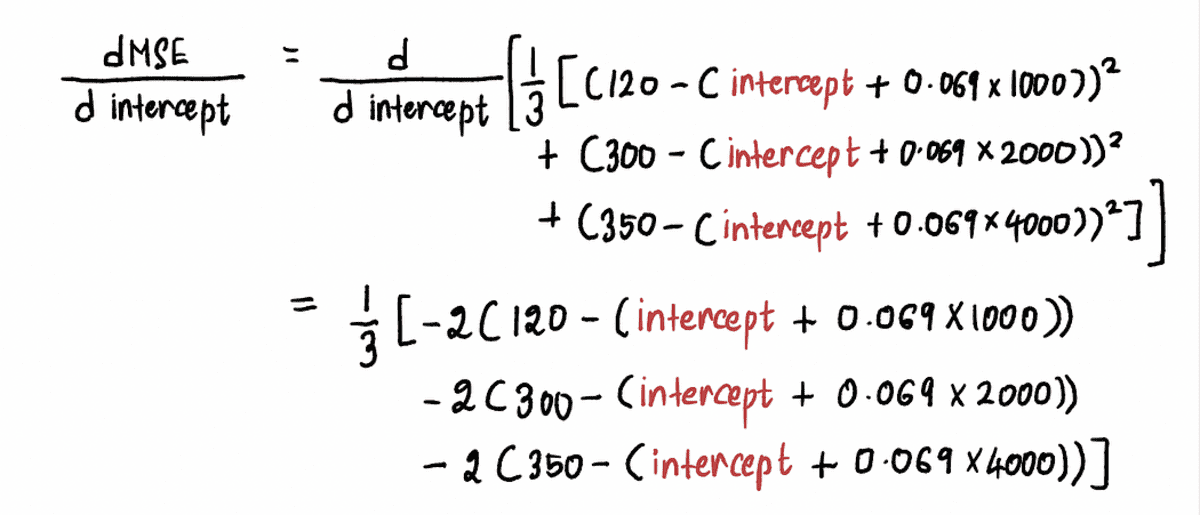
এখন খুঁজে বের করতে A বিন্দুতে গ্রেডিয়েন্ট, আমরা এর মান প্রতিস্থাপন করি পথিমধ্যে রোধ করা উপরের সমীকরণের A বিন্দুতে। থেকে পথিমধ্যে রোধ করা = 0, বিন্দু A-তে ডেরিভেটিভ হল:

 

 

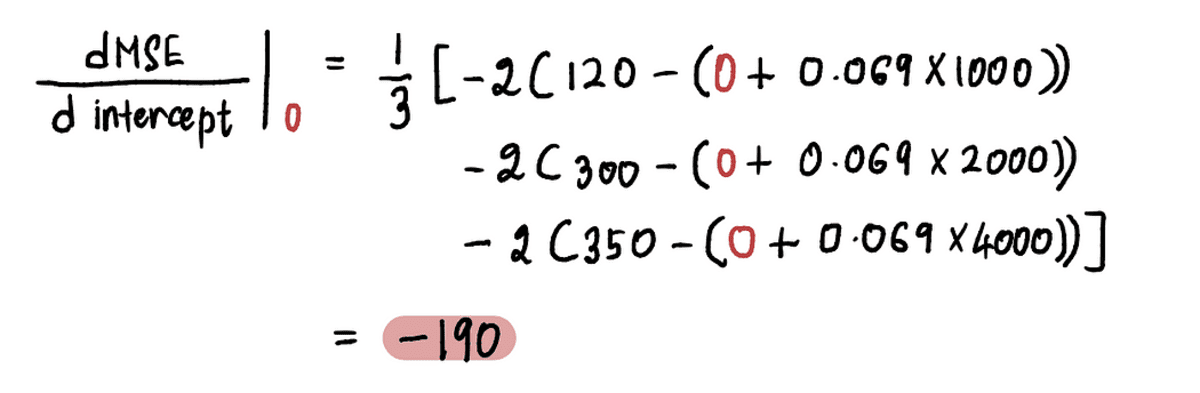
সুতরাং যখন পথিমধ্যে রোধ করা = 0, দ নতিমাত্রা =-190

লক্ষ্য করুন: আমরা যখন সর্বোত্তম মানের কাছে যাই, গ্রেডিয়েন্ট মানগুলি শূন্যের কাছে পৌঁছায়। সর্বোত্তম মানতে, গ্রেডিয়েন্টটি শূন্যের সমান। বিপরীতভাবে, আমরা সর্বোত্তম মান থেকে যত দূরে থাকব, গ্রেডিয়েন্ট তত বড় হবে।

 

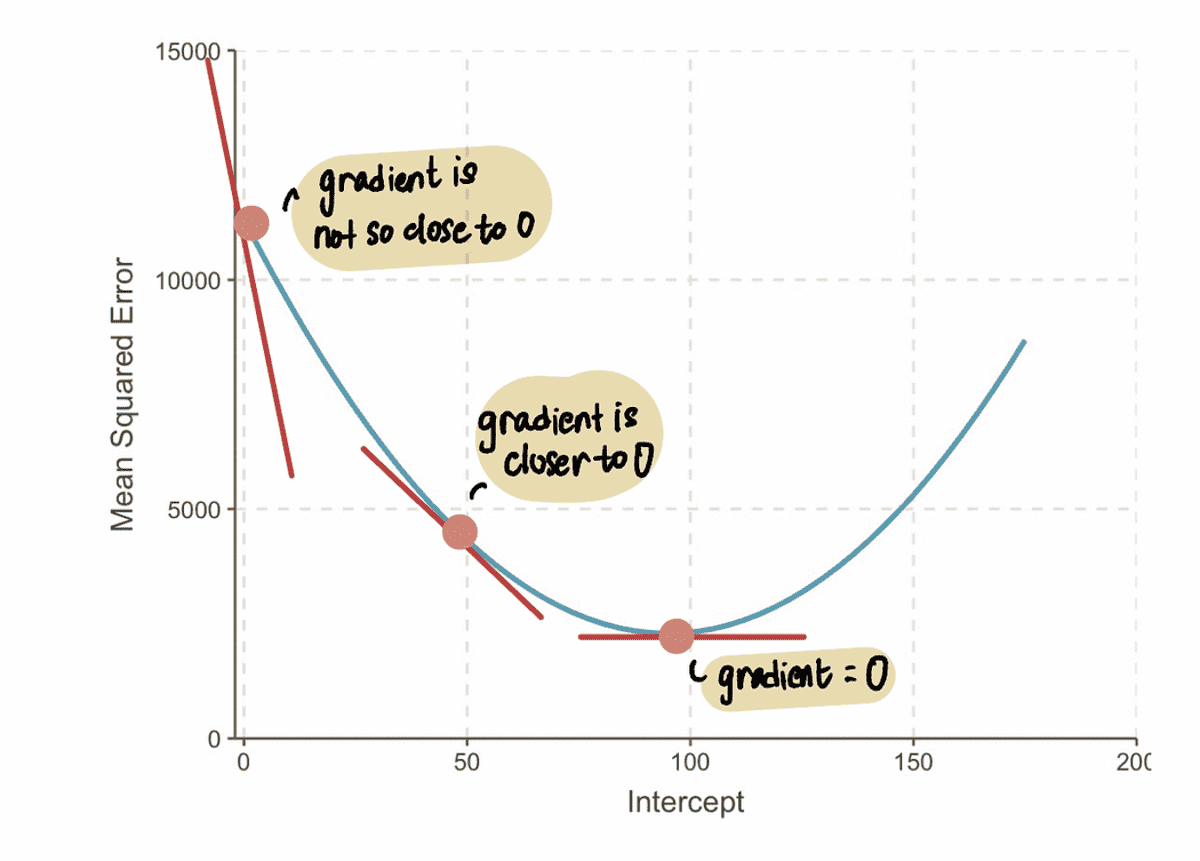
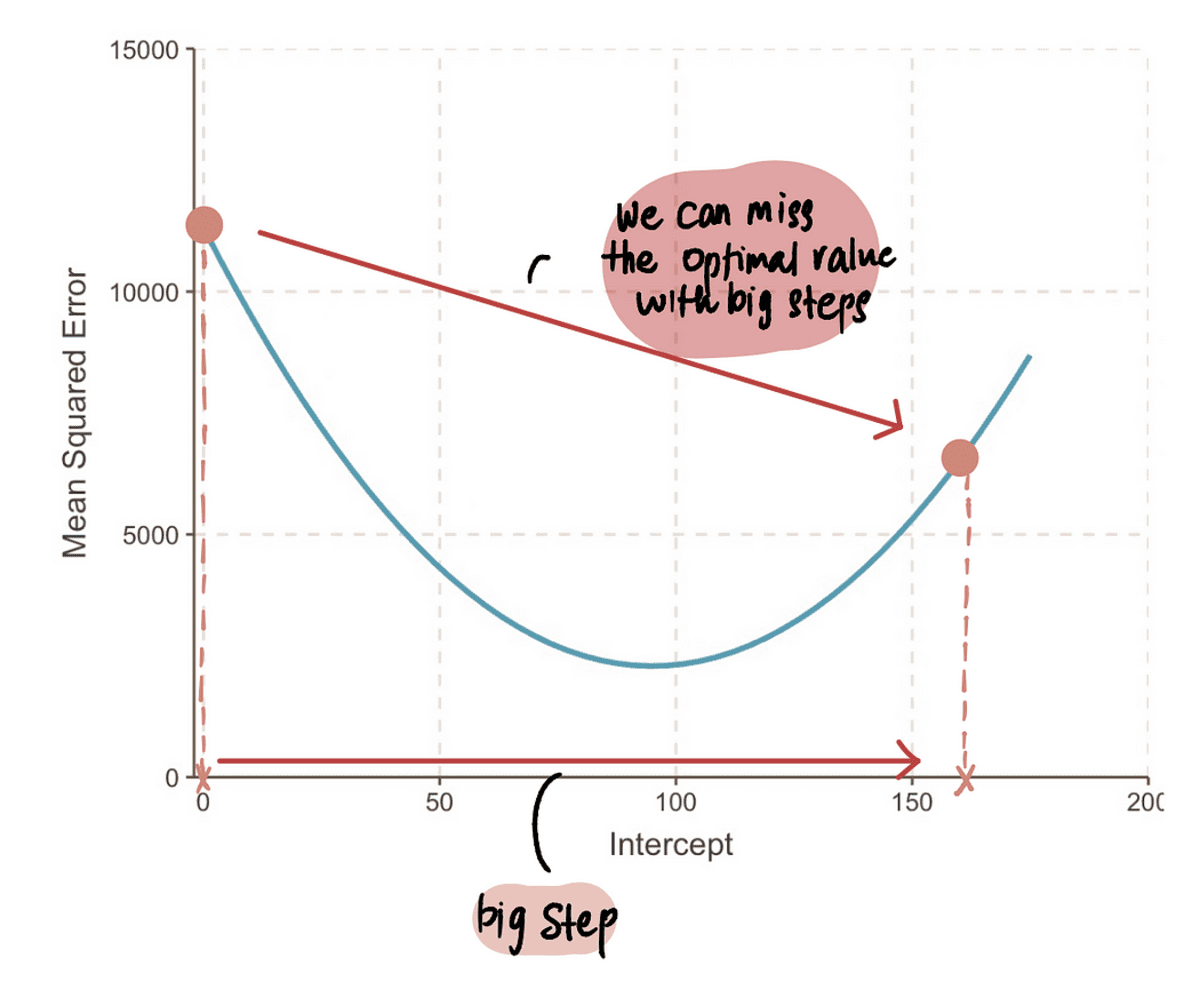
এটি থেকে, আমরা অনুমান করতে পারি যে ধাপের আকার এর সাথে সম্পর্কিত হওয়া উচিত নতিমাত্রা, যেহেতু এটি আমাদের বলে যে আমাদের একটি শিশুর পদক্ষেপ নেওয়া উচিত বা একটি বড় পদক্ষেপ নেওয়া উচিত। এর মানে হল যে যখন নতিমাত্রা বক্ররেখা 0 এর কাছাকাছি, তাহলে আমাদের শিশুর পদক্ষেপ নেওয়া উচিত কারণ আমরা সর্বোত্তম মানের কাছাকাছি। এবং যদি নতিমাত্রা আরও বড়, দ্রুত সর্বোত্তম মান পেতে আমাদের আরও বড় পদক্ষেপ নেওয়া উচিত।

লক্ষ্য করুন: যাইহোক, যদি আমরা একটি বিশাল বড় পদক্ষেপ নিই, তাহলে আমরা একটি বড় লাফ দিতে পারি এবং সর্বোত্তম পয়েন্টটি মিস করতে পারি। তাই আমাদের সতর্ক থাকতে হবে।

ধাপ 3: গ্রেডিয়েন্ট এবং শেখার হার ব্যবহার করে ধাপের আকার গণনা করুন এবং ইন্টারসেপ্ট মান আপডেট করুন

যেহেতু আমরা দেখতে পাই যে ধাপে আকার এবং নতিমাত্রা একে অপরের সমানুপাতিক হয়, ধাপে আকার গুন দ্বারা নির্ধারিত হয় নতিমাত্রা নামক একটি পূর্ব-নির্ধারিত ধ্রুবক মান দ্বারা শেখার হার:

 

 

সার্জারির  শিক্ষার হার এর মাত্রা নিয়ন্ত্রণ করে ধাপে আকার এবং নিশ্চিত করে যে নেওয়া পদক্ষেপটি খুব বড় বা খুব ছোট নয়।

অনুশীলনে, শেখার হার সাধারণত একটি ছোট ধনাত্মক সংখ্যা হয়? 0.001। কিন্তু আমাদের সমস্যার জন্য এটি 0.1 এ সেট করা যাক।

তাই যখন ইন্টারসেপ্ট 0 হয়, ধাপের আকার = গ্রেডিয়েন্ট x শিক্ষার হার = -190*0.1 = -19।

উপর ভিত্তি করে ধাপে আকার আমরা উপরে গণনা করেছি, আমরা আপডেট করি পথিমধ্যে রোধ করা (ওরফে আমাদের বর্তমান অবস্থান পরিবর্তন করুন) এই সমতুল্য সূত্রগুলির যেকোনো একটি ব্যবহার করে:

 

 

নতুন খোঁজার জন্য পথিমধ্যে রোধ করা এই ধাপে, আমরা প্রাসঙ্গিক মানগুলি প্লাগ ইন করি...

 

 

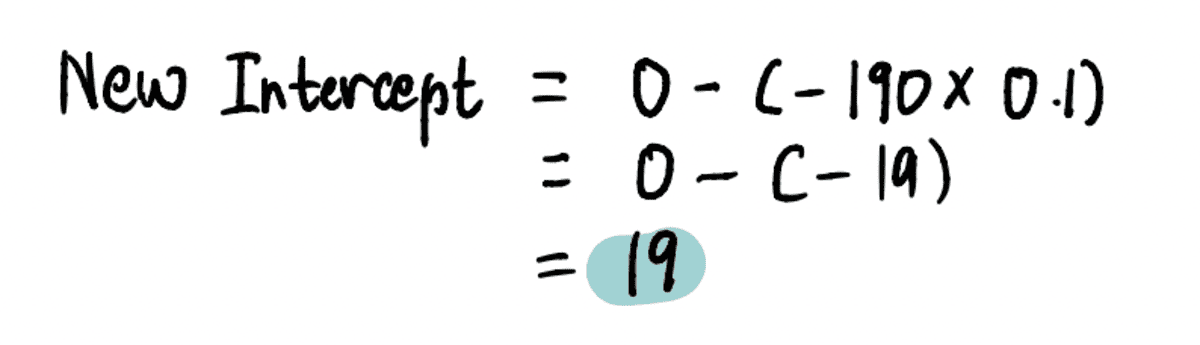
…এবং নতুন যে খুঁজে পথিমধ্যে রোধ করা = 19

এখন এই মান প্লাগ করা MSE সমীকরণ, আমরা যে খুঁজে MSE যখন পথিমধ্যে রোধ করা হল 19 = 8064.095। আমরা লক্ষ্য করেছি যে একটি বড় পদক্ষেপে, আমরা আমাদের সর্বোত্তম মানের কাছাকাছি চলে এসেছি এবং কমিয়েছি MSE.

 

 

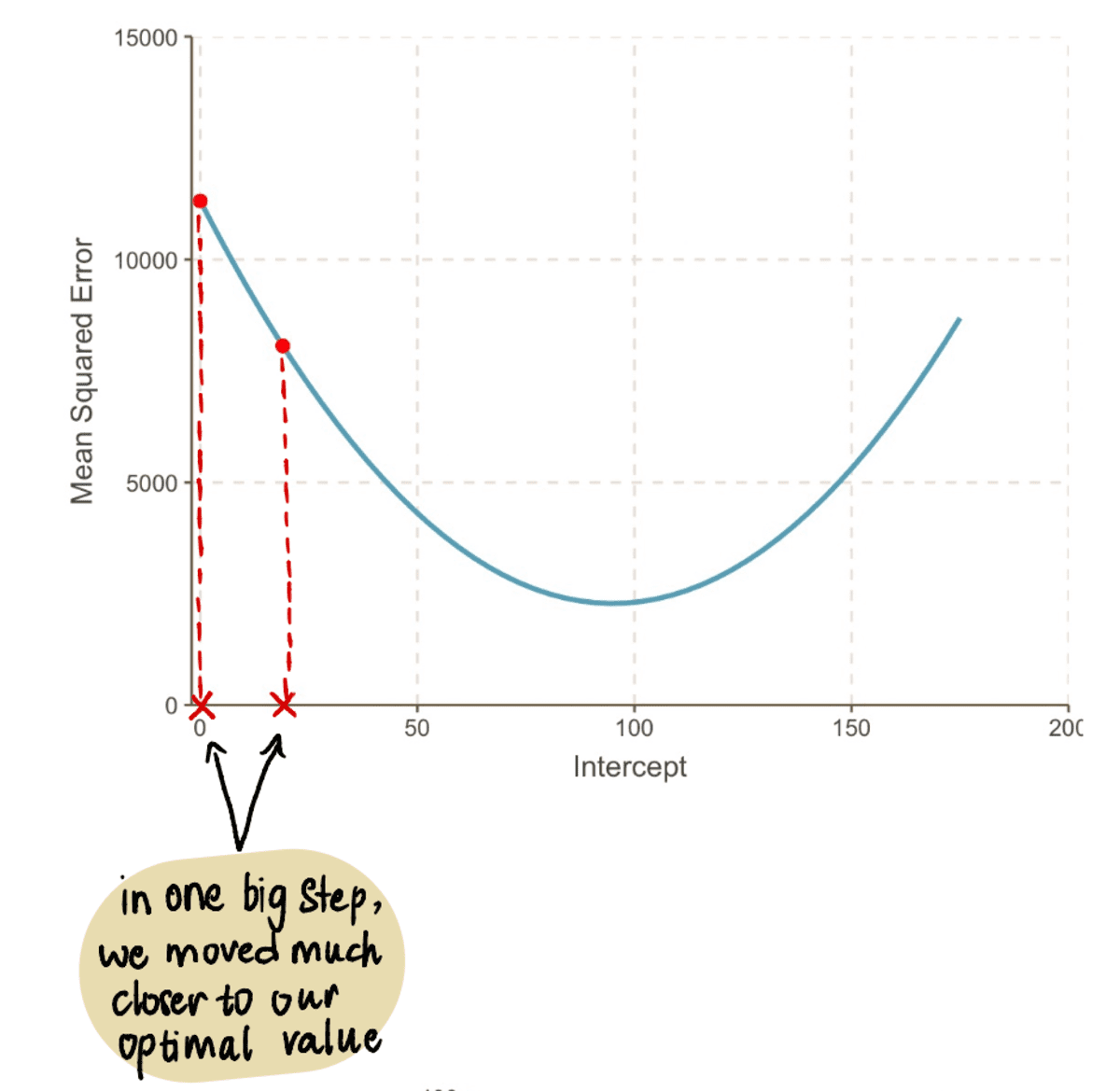
এমনকি যদি আমরা আমাদের গ্রাফের দিকে তাকাই, আমরা দেখতে পাই যে আমাদের নতুন লাইনের সাথে কতটা ভাল পথিমধ্যে রোধ করা 19 আমাদের পুরানো লাইনের তুলনায় আমাদের ডেটার সাথে মানানসই পথিমধ্যে রোধ করা 0:

 

 

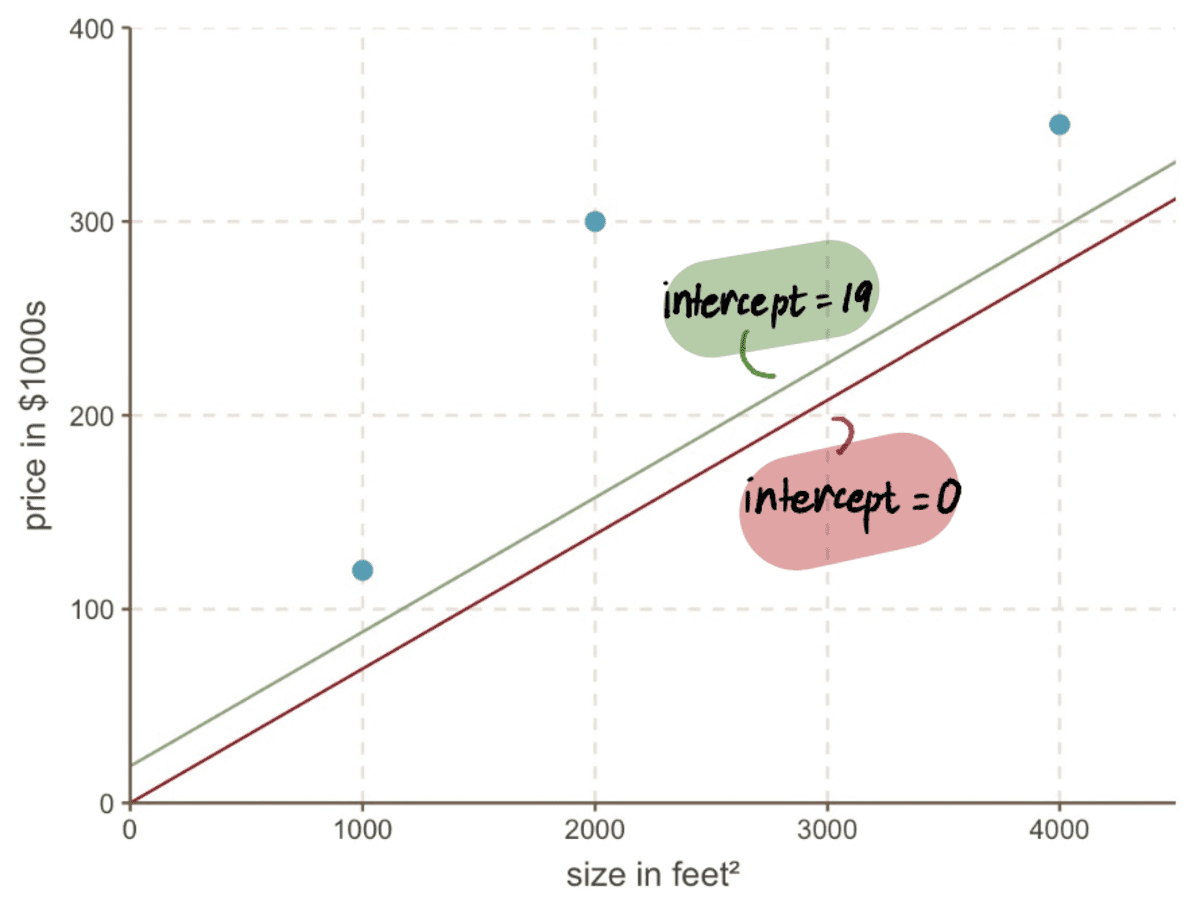
ধাপ 4: ধাপ 2-3 পুনরাবৃত্তি করুন

আমরা আপডেট ব্যবহার করে ধাপ 2 এবং 3 পুনরাবৃত্তি করি পথিমধ্যে রোধ করা মান।

যেমন নতুন থেকে পথিমধ্যে রোধ করা এই পুনরাবৃত্তির মান হল 19, নিম্নলিখিত ধাপ 2, আমরা এই নতুন পয়েন্টে গ্রেডিয়েন্ট গণনা করব:

 

 

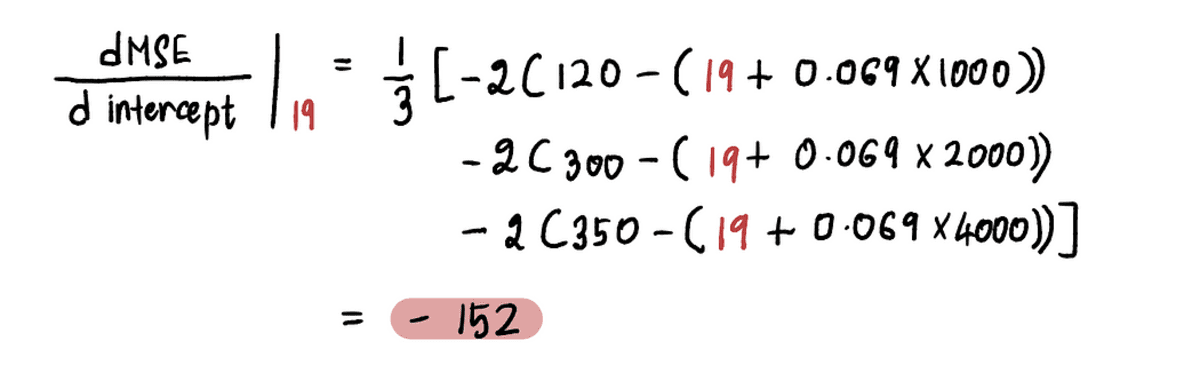
এবং আমরা যে খুঁজে নতিমাত্রা এর MSE 19 এর ইন্টারসেপ্ট মানের বক্ররেখা হল -152 (নীচের চিত্রে লাল স্পর্শক রেখা দ্বারা উপস্থাপিত)।

 

 

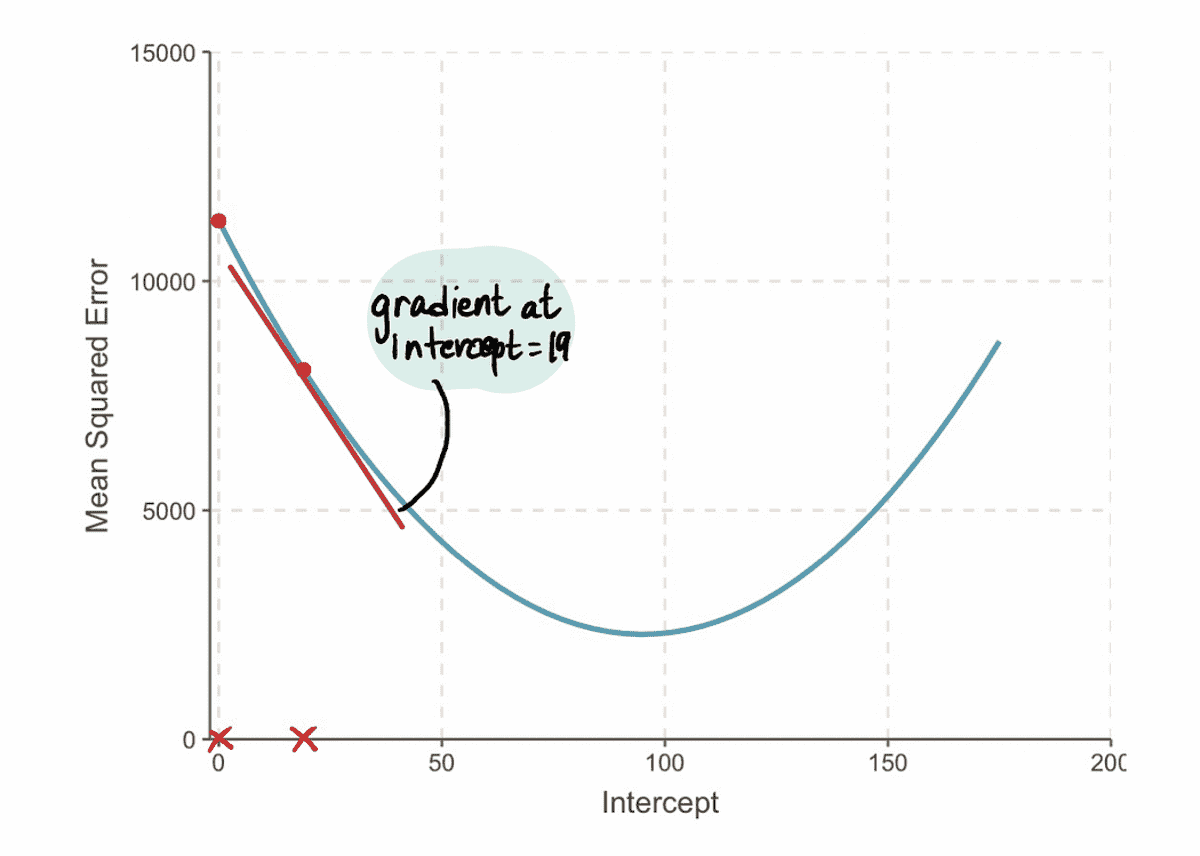
পরবর্তী, অনুযায়ী ধাপ 3, এর গণনা করা যাক ধাপে আকার:

 

 

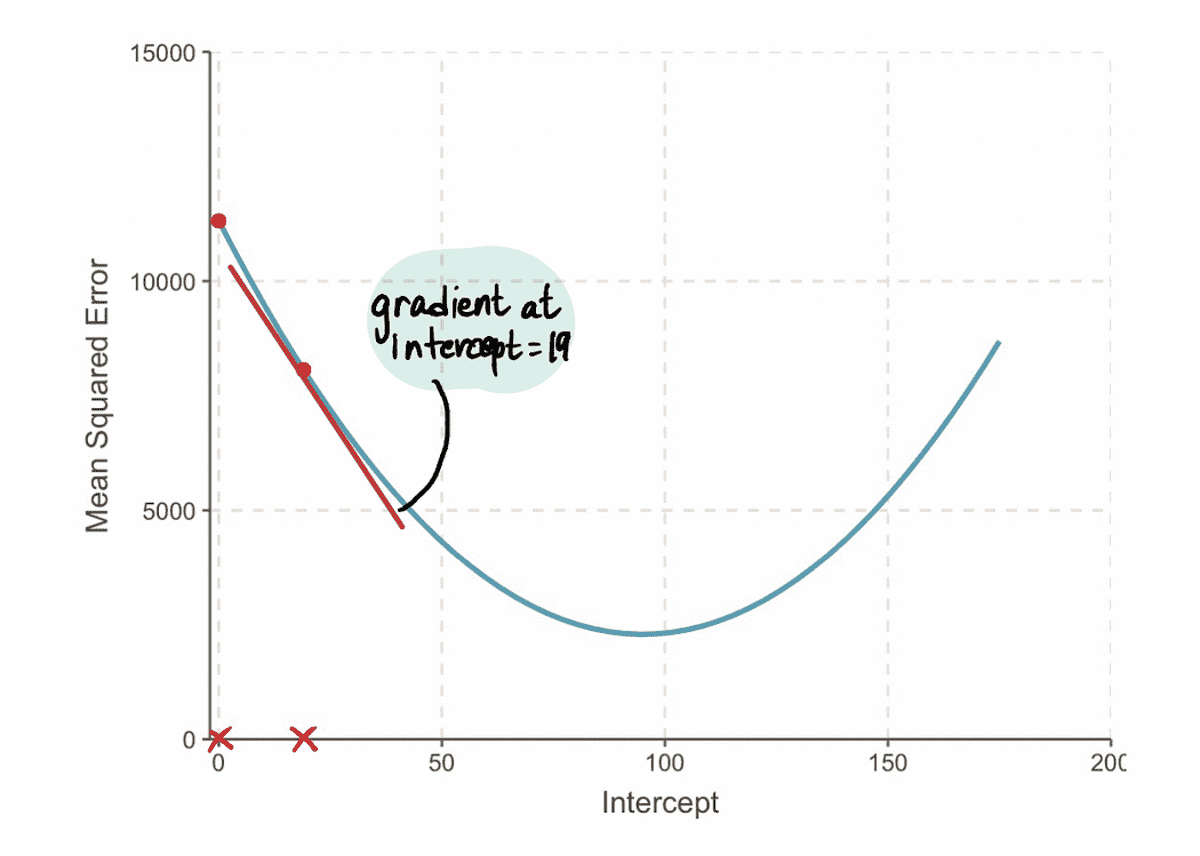
এবং পরবর্তীকালে, আপডেট করুন পথিমধ্যে রোধ করা মান:

 

 

এখন আমরা আগের লাইনের সাথে তুলনা করতে পারি পথিমধ্যে রোধ করা নতুন ইন্টারসেপ্ট 19 সহ 34.2 থেকে নতুন লাইনে…

 

 

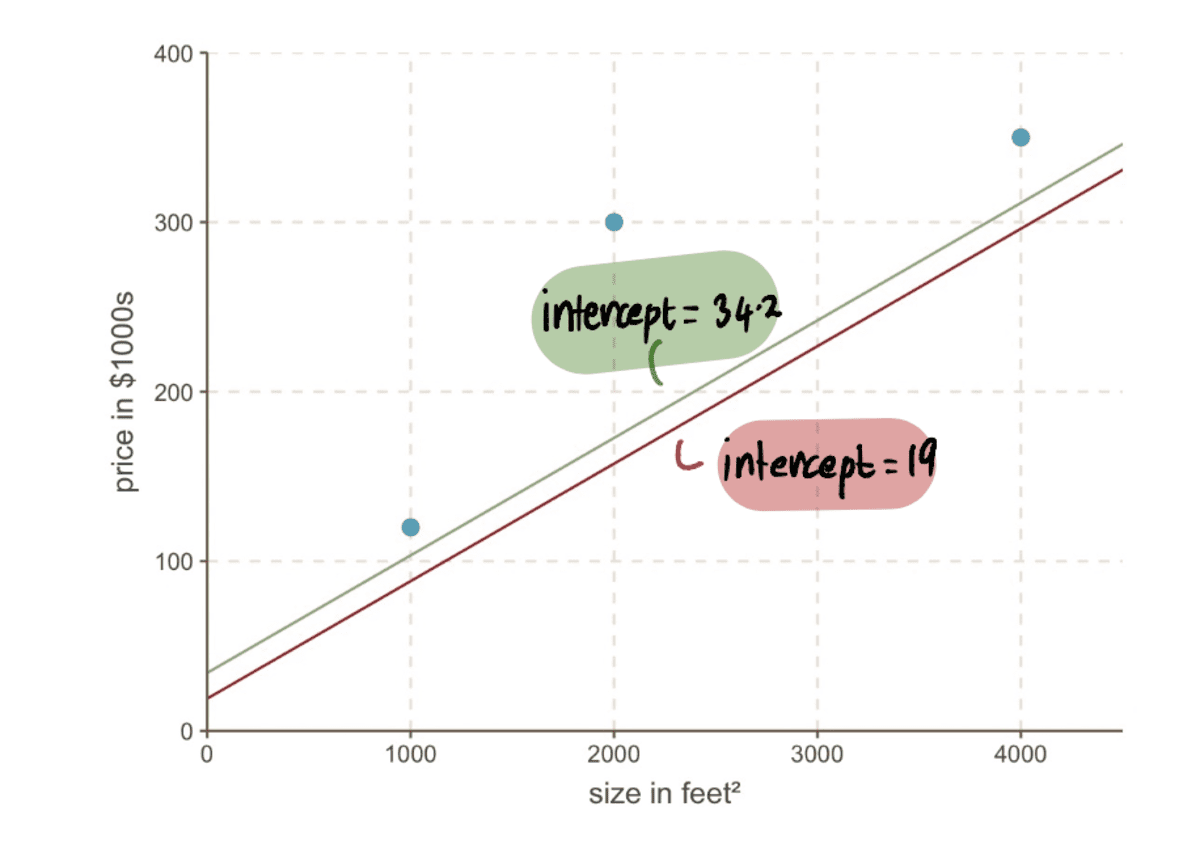
…এবং আমরা দেখতে পাচ্ছি যে নতুন লাইনটি ডেটার সাথে আরও ভালভাবে ফিট করে।

সামগ্রিকভাবে, MSE ছোট হয়ে আসছে…

 

 

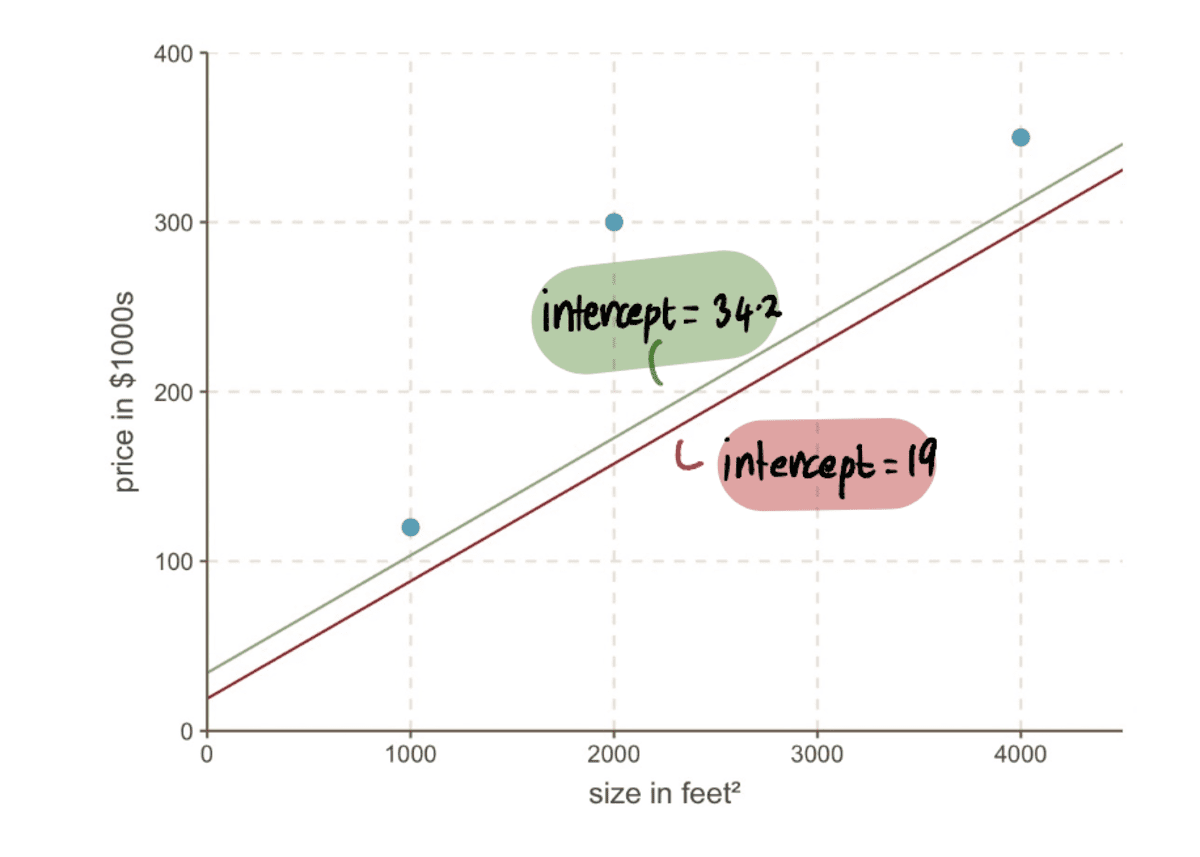
…এবং আমাদের ধাপের আকার ছোট হচ্ছে:

 

 

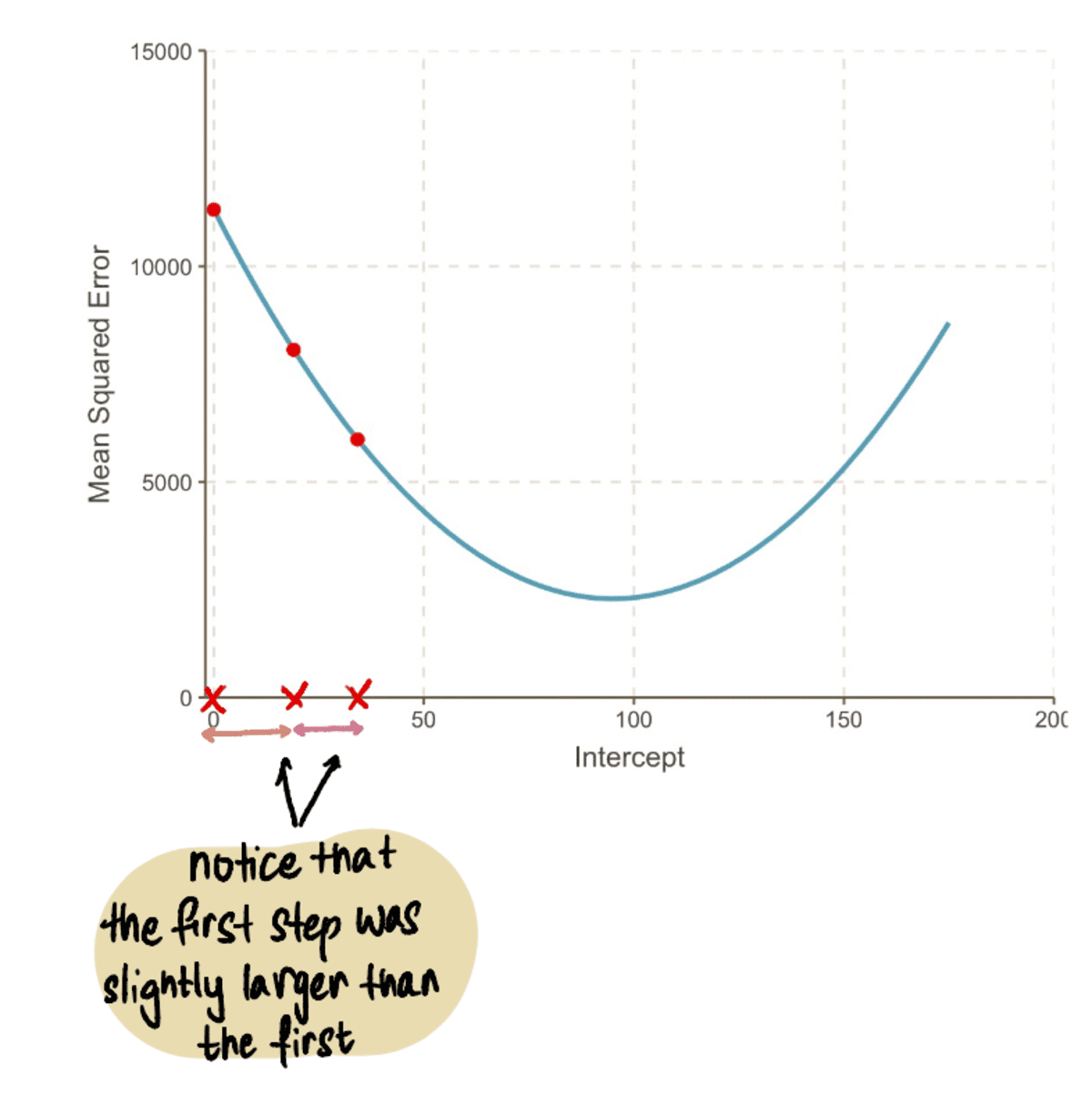
আমরা এই প্রক্রিয়াটি পুনরাবৃত্তি করে থাকি যতক্ষণ না আমরা সর্বোত্তম সমাধানের দিকে একত্রিত হই:

 

 

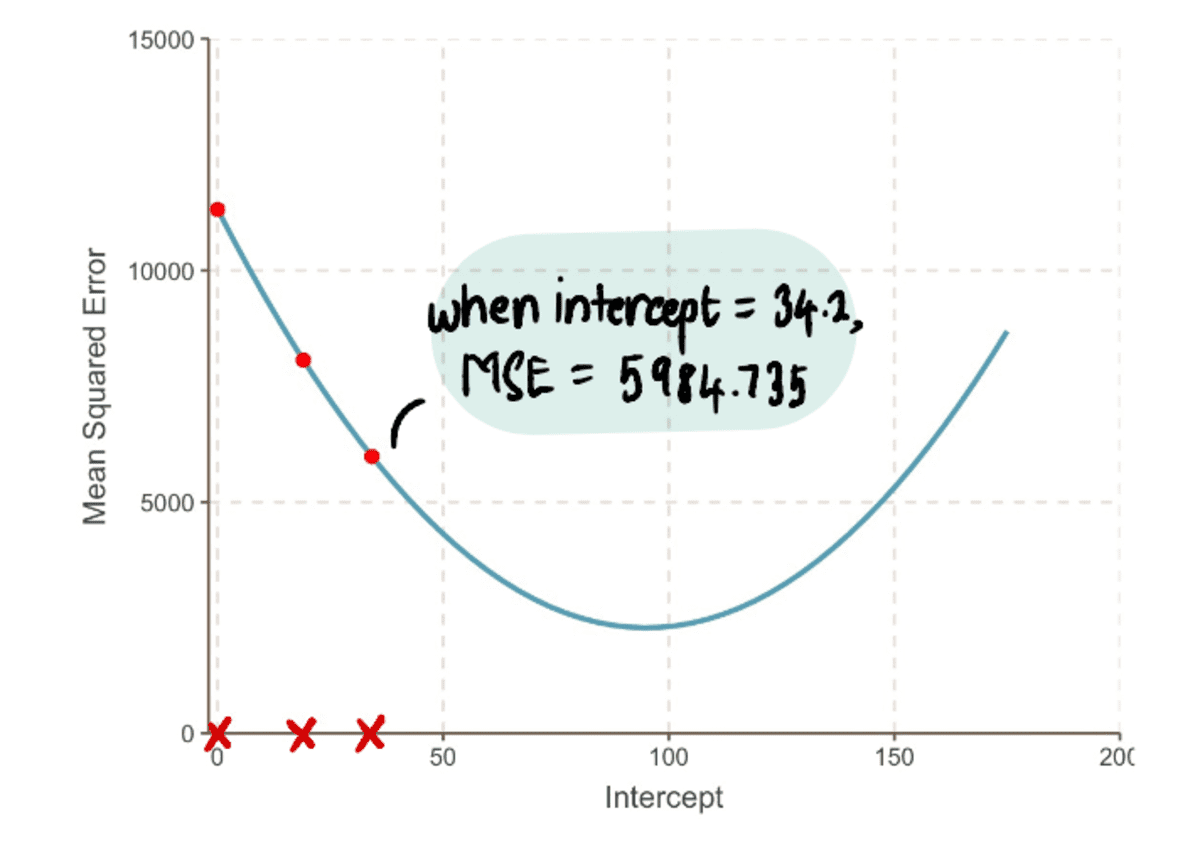
আমরা বক্ররেখার সর্বনিম্ন বিন্দুর দিকে অগ্রসর হওয়ার সাথে সাথে আমরা লক্ষ্য করি যে ধাপে আকার ক্রমশ ছোট হয়ে যায়। 13টি ধাপের পর, গ্রেডিয়েন্ট ডিসেন্ট অ্যালগরিদম অনুমান করে পথিমধ্যে রোধ করা মান 95 হতে হবে। যদি আমাদের একটি ক্রিস্টাল বল থাকে, তাহলে এটি সর্বনিম্ন বিন্দু হিসাবে নিশ্চিত করা হবে MSE বক্ররেখা এবং আমরা যে ব্রুট ফোর্স পদ্ধতিতে দেখেছি তার তুলনায় এই পদ্ধতিটি কীভাবে আরও কার্যকর তা দেখতে পরিষ্কার। আগের প্রবন্ধে.

এখন আমরা আমাদের সর্বোত্তম মান আছে পথিমধ্যে রোধ করা, লিনিয়ার রিগ্রেশন মডেল হল:

 

 

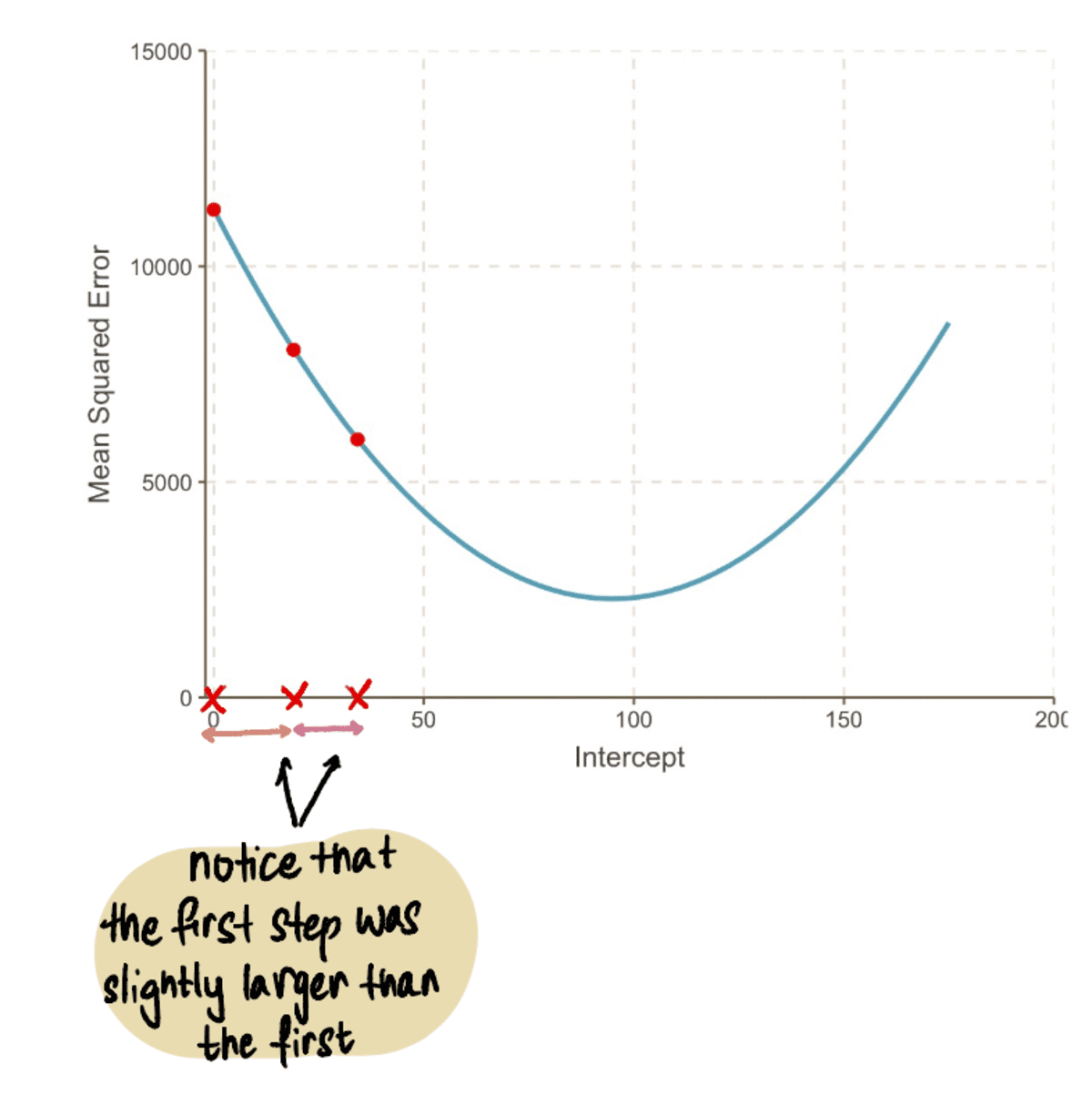
এবং রৈখিক রিগ্রেশন লাইন এই মত দেখায়:

 

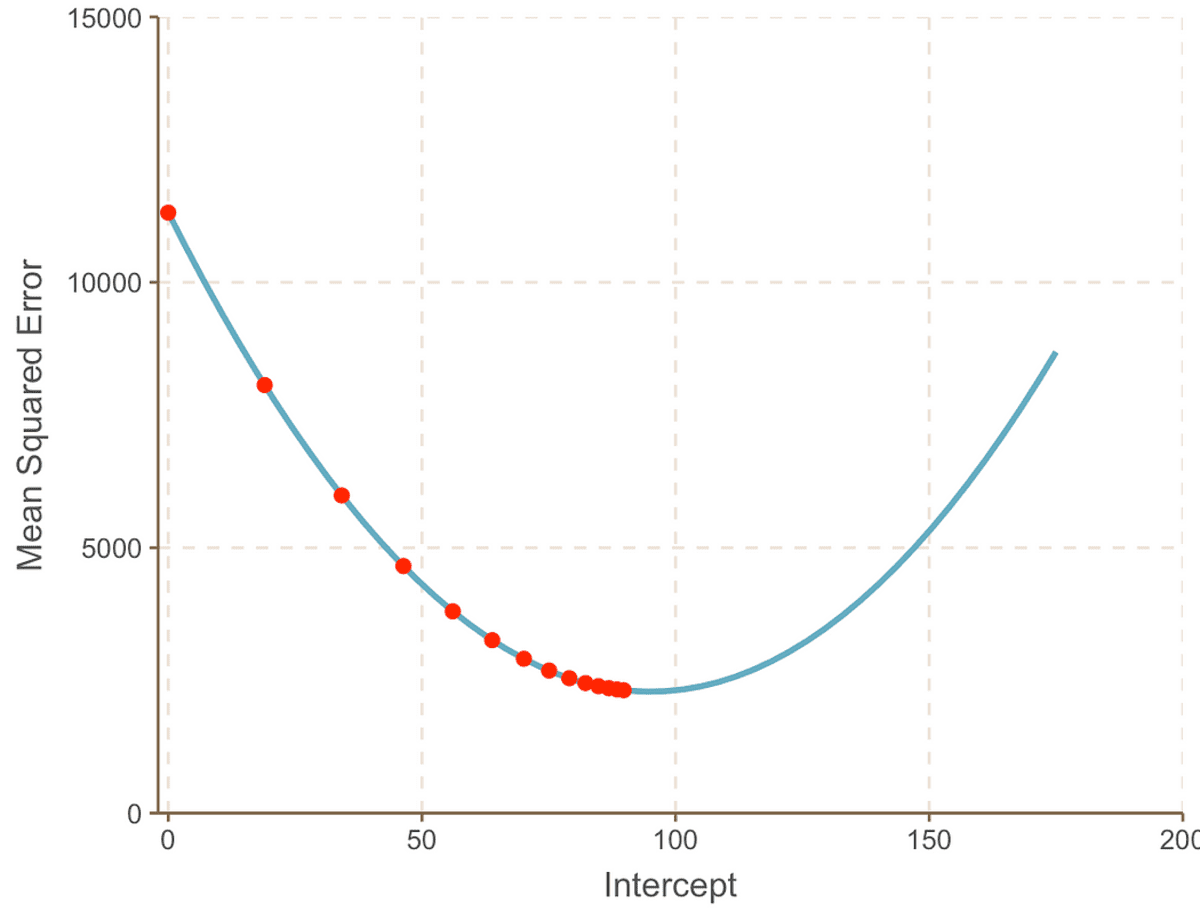
ইন্টারসেপ্ট = 95 এবং ঢাল = 0.069 সহ সেরা ফিটিং লাইন

 

অবশেষে, আমাদের বন্ধু মার্কের প্রশ্নে ফিরে যাচ্ছি — তার 2400 ফুট² বাড়িটি কী মূল্যে বিক্রি করা উচিত?

 

 

উপরের সমীকরণে 2400 ফুট² ঘরের আকার প্লাগ ইন করুন...

 

 

…এবং ভয়েলা। আমরা আমাদের অযথা উদ্বিগ্ন বন্ধু মার্ককে বলতে পারি যে তার আশেপাশের 3টি বাড়ির উপর ভিত্তি করে, তার প্রায় $260,600-এ তার বাড়ি বিক্রি করতে দেখা উচিত।

এখন যেহেতু আমাদের ধারণাগুলির একটি দৃঢ় বোঝাপড়া আছে, চলুন যেকোন দীর্ঘস্থায়ী প্রশ্নের উত্তর দিয়ে একটি দ্রুত প্রশ্নোত্তর সেশ করি।

গ্রেডিয়েন্ট খোঁজা আসলে কাজ করে কেন?

এটি ব্যাখ্যা করার জন্য, একটি দৃশ্যকল্প বিবেচনা করুন যেখানে আমরা বক্ররেখা C এর ন্যূনতম বিন্দুতে পৌঁছানোর চেষ্টা করছি, হিসাবে চিহ্নিত x*. এবং আমরা বর্তমানে A বিন্দুতে আছি x, এর বাম দিকে অবস্থিত x*:

 

 

যদি আমরা সাপেক্ষে A বিন্দুতে বক্ররেখার ডেরিভেটিভ নিই x, হিসাবে উপস্থাপিত dC(x)/dx, আমরা একটি নেতিবাচক মান পাই (এর মানে হল নতিমাত্রা নিচের দিকে ঢালু) আমরা আরও লক্ষ্য করি যে পৌঁছানোর জন্য আমাদের ডানদিকে যেতে হবে x*. এইভাবে, আমাদের বাড়াতে হবে x সর্বনিম্ন পৌঁছাতে এক্স*.

 

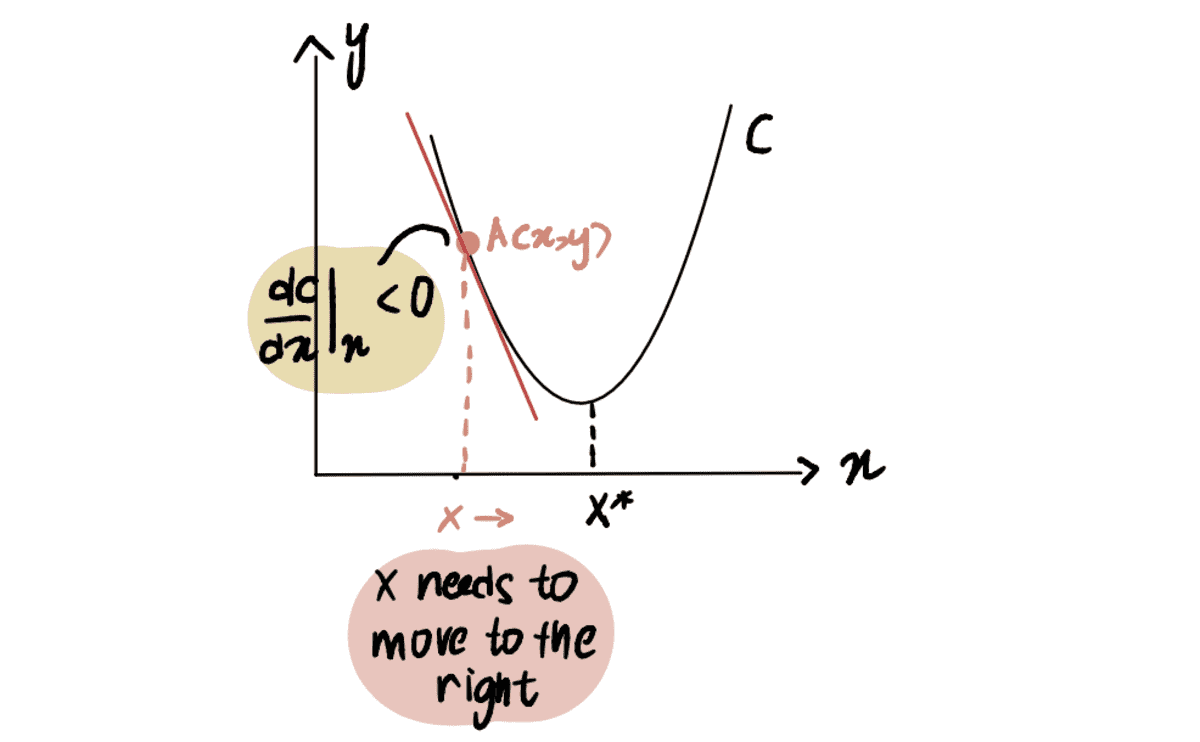
লাল রেখা, বা গ্রেডিয়েন্ট, নিচের দিকে ঢালু => একটি নেতিবাচক গ্রেডিয়েন্ট

 
 

থেকে dC(x)/dx নেতিবাচক, x-??*dC(x)/dx থেকে বড় হবে x, এইভাবে দিকে চলন্ত x*.

একইভাবে, যদি আমরা ন্যূনতম বিন্দু x* এর ডানদিকে অবস্থিত A বিন্দুতে থাকি, তাহলে আমরা a পাব ধনাত্মক নতিমাত্রা (নতিমাত্রা উপরের দিকে ঢালু) dC(x)/dx.

 

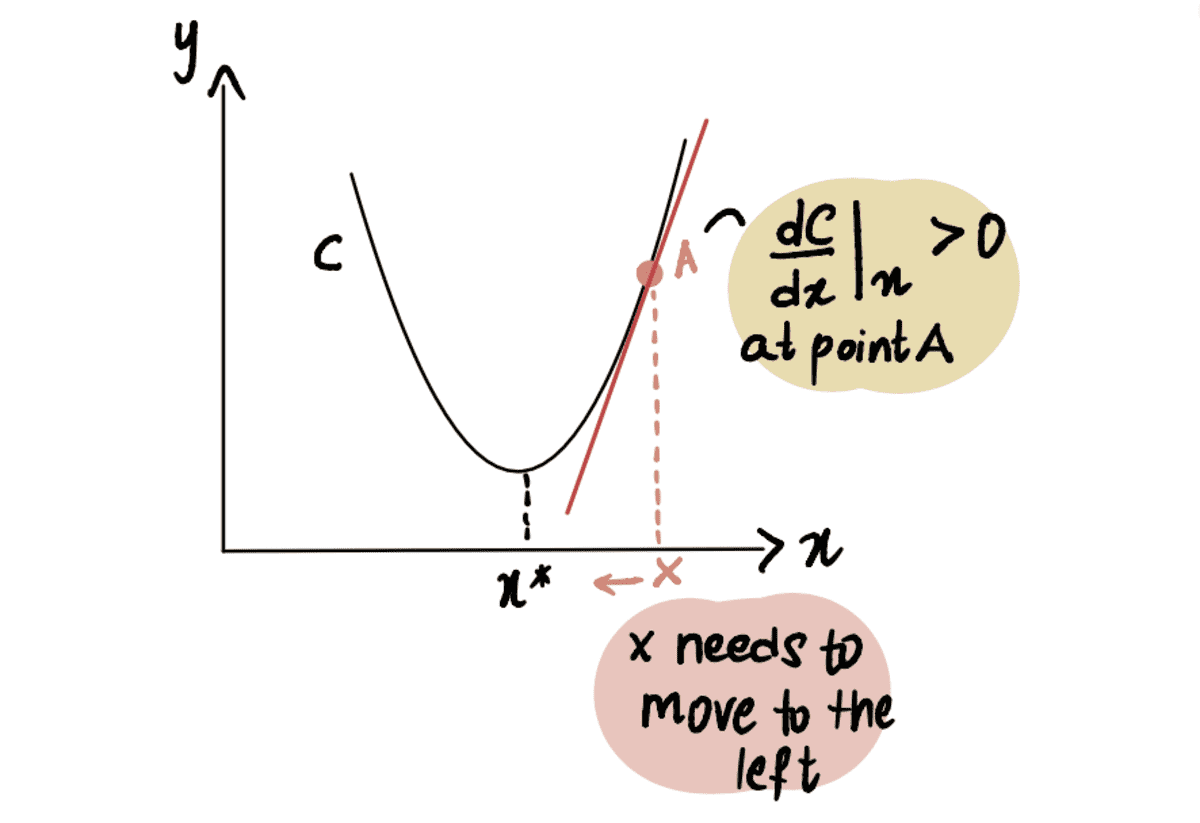
লাল রেখা, বা গ্রেডিয়েন্ট, উপরের দিকে ঢালু => একটি ধনাত্মক গ্রেডিয়েন্ট

 

So x-??*dC(x)/dx থেকে কম হবে x, এইভাবে দিকে চলন্ত x*.

গ্রেডিয়েন্ট ডিসেন্ট কিভাবে জানে কখন পদক্ষেপ নেওয়া বন্ধ করতে হবে?

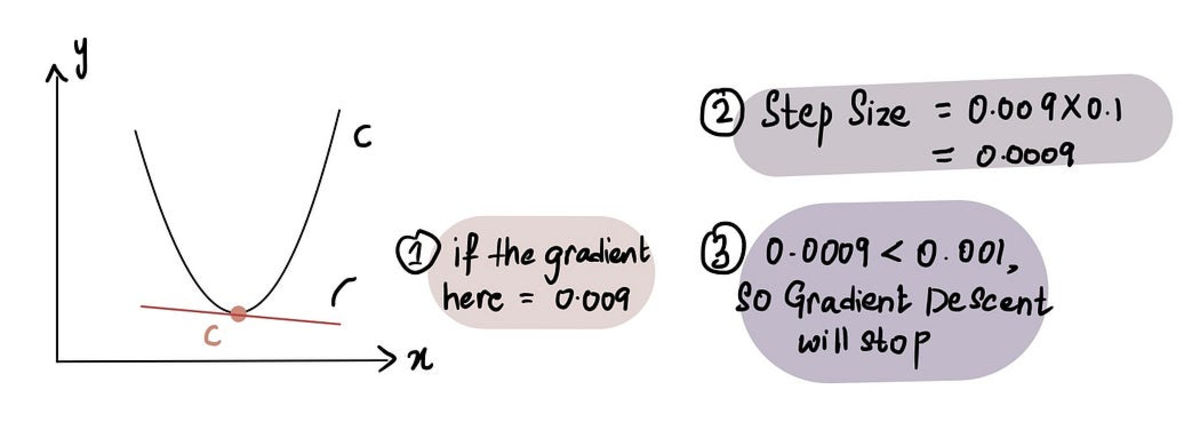
গ্রেডিয়েন্ট ডিসেন্ট থামে যখন ধাপে আকার 0 এর খুব কাছাকাছি। পূর্বে আলোচনা করা হয়েছে, সর্বনিম্ন পয়েন্টে নতিমাত্রা হল 0 এবং আমরা ন্যূনতম কাছে যাওয়ার সাথে সাথে, নতিমাত্রা 0 এর কাছাকাছি। অতএব, যখন নতিমাত্রা একটি বিন্দুতে 0 এর কাছাকাছি বা সর্বনিম্ন বিন্দুর কাছাকাছি, ধাপে আকার এছাড়াও 0 এর কাছাকাছি হবে, এটি নির্দেশ করে যে অ্যালগরিদম সর্বোত্তম সমাধানে পৌঁছেছে।

 

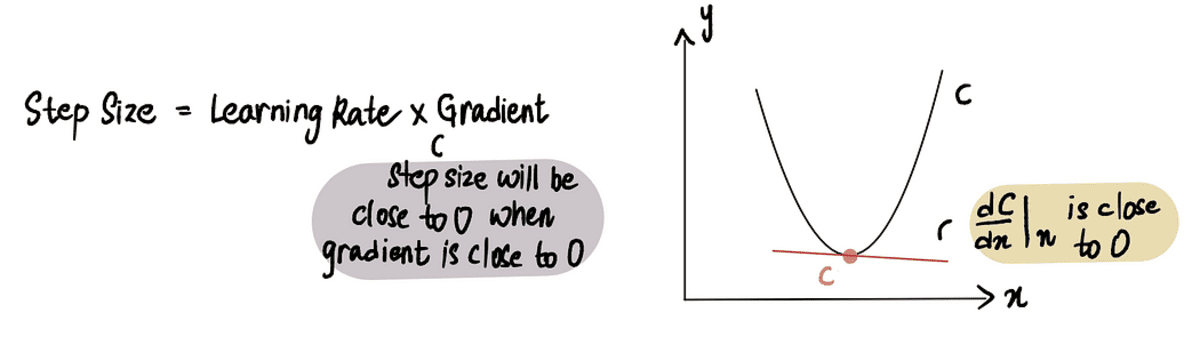
যখন আমরা ন্যূনতম বিন্দুর কাছাকাছি থাকি, গ্রেডিয়েন্ট 0-এর কাছাকাছি থাকে এবং পরবর্তীকালে ধাপের আকার 0-এর কাছাকাছি থাকে

অনুশীলনে সর্বনিম্ন ধাপের আকার = 0.001 বা ছোট

 

বলা হচ্ছে, গ্রেডিয়েন্ট ডিসেন্টের মধ্যে একটি সীমাও অন্তর্ভুক্ত রয়েছে যেটি হাল ছেড়ে দেওয়ার আগে এটি গ্রহণ করবে ধাপের সর্বোচ্চ সংখ্যা.

অনুশীলনে, ধাপের সর্বোচ্চ সংখ্যা = 1000 বা তার বেশি

তাই এমনকি যদি ধাপে আকার থেকে বড় ন্যূনতম ধাপের আকার, যদি এর চেয়ে বেশি থাকে ধাপের সর্বোচ্চ সংখ্যা, গ্রেডিয়েন্ট ডিসেন্ট বন্ধ হবে।

যদি ন্যূনতম পয়েন্ট সনাক্ত করা আরও চ্যালেঞ্জিং হয়?

এখন পর্যন্ত, আমরা এমন একটি বক্ররেখা নিয়ে কাজ করছি যেখানে ন্যূনতম বিন্দু চিহ্নিত করা সহজ (এই ধরনের বক্ররেখাকে বলা হয় উত্তল) কিন্তু আমাদের যদি এমন একটি বক্ররেখা থাকে যা ততটা সুন্দর না হয় (প্রযুক্তিগতভাবে ওরফে অ-উত্তল) এবং এই মত দেখায়:

 

 

এখানে, আমরা দেখতে পাচ্ছি যে পয়েন্ট B হল বিশ্বব্যাপী সর্বনিম্ন (প্রকৃত নূন্যতম), এবং পয়েন্ট A এবং C হল স্থানীয় ন্যূনতম (বিন্দু যা বিভ্রান্ত হতে পারে বিশ্বব্যাপী সর্বনিম্ন কিন্তু নয়) তাই যদি একটি ফাংশন একাধিক আছে স্থানীয় ন্যূনতম এবং একটি বিশ্বব্যাপী সর্বনিম্ন, এটা নিশ্চিত নয় যে গ্রেডিয়েন্ট ডিসেন্ট খুঁজে পাবে বিশ্বব্যাপী সর্বনিম্ন. তদুপরি, কোন স্থানীয় সর্বনিম্ন এটি খুঁজে পায় তা প্রাথমিক অনুমানের অবস্থানের উপর নির্ভর করবে (যেমনটিতে দেখা গেছে ধাপ 1 গ্রেডিয়েন্ট ডিসেন্টের)।

 

 

উপরের এই অ-উত্তল বক্ররেখাটিকে উদাহরণ হিসাবে নিলে, যদি প্রাথমিক অনুমানটি ব্লক A বা ব্লক C-তে হয়, গ্রেডিয়েন্ট ডিসেন্ট ঘোষণা করবে যে ন্যূনতম বিন্দুটি যথাক্রমে স্থানীয় সর্বনিম্ন A বা C-তে, যখন বাস্তবে এটি B-তে থাকে। শুধুমাত্র যখন প্রাথমিক অনুমান B ব্লকে, অ্যালগরিদম বিশ্বব্যাপী সর্বনিম্ন B খুঁজে পাবে।

এখন প্রশ্ন হল - কিভাবে আমরা একটি ভাল প্রাথমিক অনুমান করতে পারি?

সহজ উত্তর: ট্রায়াল এবং ত্রুটি. ধরনের.

এত সহজ উত্তর নয়: উপরের গ্রাফ থেকে, যদি আমাদের সর্বনিম্ন অনুমান x 0 ছিল যেহেতু এটি ব্লক A-তে রয়েছে, এটি স্থানীয় ন্যূনতম A-তে নিয়ে যাবে। সুতরাং, আপনি দেখতে পাচ্ছেন, বেশিরভাগ ক্ষেত্রে 0 একটি ভাল প্রাথমিক অনুমান নাও হতে পারে। একটি সাধারণ অভ্যাস হল x এর সমস্ত সম্ভাব্য মানের পরিসরে অভিন্ন বন্টনের উপর ভিত্তি করে একটি র্যান্ডম ফাংশন প্রয়োগ করা। উপরন্তু, যদি সম্ভব হয়, বিভিন্ন প্রাথমিক অনুমান সহ অ্যালগরিদম চালানো এবং তাদের ফলাফলের তুলনা করা অনুমানগুলি একে অপরের থেকে উল্লেখযোগ্যভাবে আলাদা কিনা তা অন্তর্দৃষ্টি প্রদান করতে পারে। এটি বিশ্বব্যাপী ন্যূনতমকে আরও দক্ষতার সাথে সনাক্ত করতে সহায়তা করে।

ঠিক আছে, আমরা প্রায় চলে এসেছি। শেষ প্রশ্ন.

যদি আমরা একাধিক সর্বোত্তম মান খুঁজে বের করার চেষ্টা করছি?

এখন পর্যন্ত, আমরা শুধুমাত্র সর্বোত্তম ইন্টারসেপ্ট মান খুঁজে বের করার উপর দৃষ্টি নিবদ্ধ করেছিলাম কারণ আমরা জাদুকরীভাবে জানতাম ঢাল রৈখিক রিগ্রেশনের মান হল 0.069। কিন্তু যদি একটি ক্রিস্টাল বল না থাকে এবং সর্বোত্তম জানি না তাহলে কি হবে ঢাল মান? তারপরে আমাদের ঢাল এবং ইন্টারসেপ্ট মান উভয়কেই অপ্টিমাইজ করতে হবে, যেমন প্রকাশ করা হয়েছে x? এবং x? যথাক্রমে.

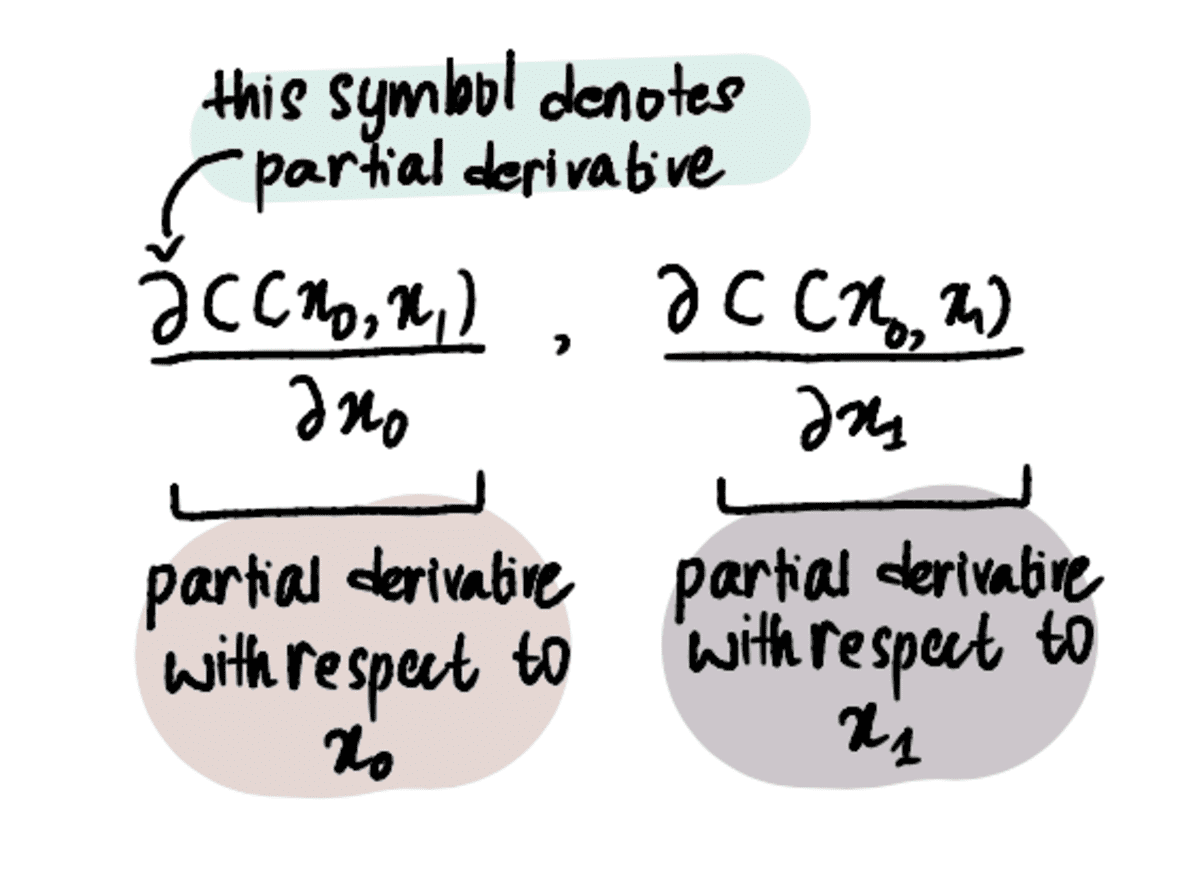
এটি করার জন্য, আমাদের অবশ্যই ডেরিভেটিভের পরিবর্তে আংশিক ডেরিভেটিভ ব্যবহার করতে হবে।

দ্রষ্টব্য: আংশিক ডেরিভেটগুলি নিয়মিত পুরানো ডেরিভেটগুলির মতো একইভাবে গণনা করা হয়, তবে আলাদাভাবে চিহ্নিত করা হয় কারণ আমাদের একাধিক পরিবর্তনশীল রয়েছে যার জন্য আমরা অপ্টিমাইজ করার চেষ্টা করছি৷ তাদের সম্পর্কে আরও জানতে, এটি পড়ুন প্রবন্ধ বা এই দেখুন ভিডিও.

যাইহোক, প্রক্রিয়াটি তুলনামূলকভাবে একটি একক মান অপ্টিমাইজ করার মতোই থাকে। খরচ ফাংশন (যেমন MSE) এখনও সংজ্ঞায়িত করা আবশ্যক এবং গ্রেডিয়েন্ট ডিসেন্ট অ্যালগরিদম অবশ্যই প্রয়োগ করতে হবে, তবে উভয় x এর জন্য আংশিক ডেরিভেটিভস খোঁজার যুক্ত পদক্ষেপের সাথে? এবং x?

ধাপ 1: x₀ এবং x₁ এর জন্য প্রাথমিক অনুমান করুন

ধাপ 2: এই বিন্দুতে x₀ এবং x₁ এর সাপেক্ষে আংশিক ডেরিভেটিভ খুঁজুন

 

 

ধাপ 3: আংশিক ডেরিভেটিভ এবং শেখার হারের উপর ভিত্তি করে একই সাথে x₀ এবং x₁ আপডেট করুন

 

 

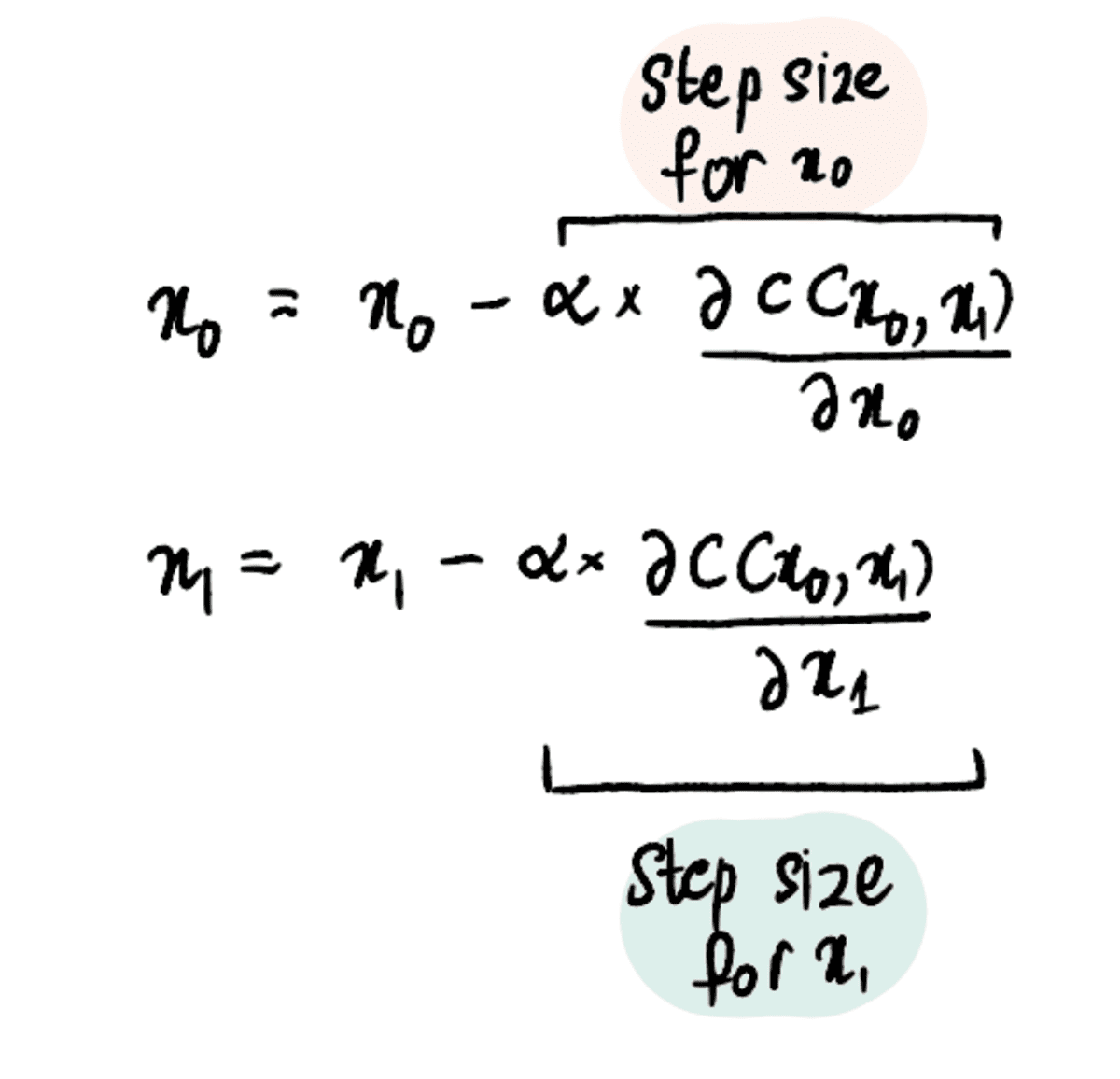
ধাপ 4: ধাপ 2-3 পুনরাবৃত্তি করুন যতক্ষণ না ধাপের সর্বাধিক সংখ্যা না পৌঁছায় বা ধাপের আকার ন্যূনতম ধাপের আকার থেকে কম হয়

এবং আমরা অপ্টিমাইজ করার জন্য এই ধাপগুলিকে 3, 4, এমনকি 100 মানেরও এক্সট্রাপোলেট করতে পারি।

উপসংহারে, গ্রেডিয়েন্ট ডিসেন্ট হল একটি শক্তিশালী অপ্টিমাইজেশান অ্যালগরিদম যা আমাদেরকে দক্ষতার সাথে সর্বোত্তম মান পৌঁছাতে সাহায্য করে। গ্রেডিয়েন্ট ডিসেন্ট অ্যালগরিদম অন্যান্য অনেক অপ্টিমাইজেশান সমস্যার ক্ষেত্রে প্রয়োগ করা যেতে পারে, এটি ডেটা বিজ্ঞানীদের অস্ত্রাগারে থাকা একটি মৌলিক হাতিয়ার করে তোলে। এখন বড় এবং ভাল অ্যালগরিদম সম্মুখের!

 
 
শ্রেয়া রাও সাধারণ মানুষের পদে মেশিন লার্নিং অ্যালগরিদমগুলি চিত্রিত করুন এবং ব্যাখ্যা করুন।

 
মূল। অনুমতি নিয়ে পোস্ট করা।
 

• এসইও চালিত বিষয়বস্তু এবং পিআর বিতরণ। আজই পরিবর্ধিত পান।
• প্লেটোব্লকচেন। Web3 মেটাভার্স ইন্টেলিজেন্স। জ্ঞান প্রসারিত. এখানে প্রবেশ করুন.
• উত্স: https://www.kdnuggets.com/2023/03/back-basics-part-dos-gradient-descent.html?utm_source=rss&utm_medium=rss&utm_campaign=back-to-basics-part-dos-gradient-descent