Einleitung
Im Dezember 1977 ein Revolutionär Krepppapier leise erschien in der Journal d’Analyse Mathematique, eine Fachzeitschrift für Mathematik. Der Autor, Hillel Fürstenberg, behauptete keine aufregenden – oder gar neuen – Ergebnisse. Er hatte einfach einen Beweis für einen Satz angeboten, den ein anderer Mathematiker, Endre Szemerédi, bereits zwei Jahre zuvor bewiesen hatte.
Trotzdem hinterließ Fürstenbergs Arbeit einen bleibenden Eindruck in der Mathematik. Seine neue Argumentation enthielt einen Kern von Einsicht mit weitreichenden Konsequenzen: Man könnte Probleme wie das, das Szemerédi gelöst hatte, über Mengen von ganzen Zahlen, in Fragen über sich im Raum bewegende Punkte umformulieren.
In den folgenden Jahren wurden Fürstenbergs Techniken immer wieder verwendet, nach und nach angepasst und verbessert. Anfang dieses Jahres wurden sie aufgeladen und erschienen in zwei neuen Artikeln, die unendliche Muster in Mengen von ganzen Zahlen aufdecken – und damit sprunghaft an Szemerédis inzwischen 47 Jahre altem Theorem vorbeikommen.
Fürstenbergs Beweis
Szemerédi hatte Mengen untersucht, die einen „positiven Bruch“ aller ganzen Zahlen enthalten. Nehmen Sie zum Beispiel die Menge, die alle Vielfachen von 5 enthält. Wenn Sie sich immer größere Schwaden des Zahlenstrahls ansehen, tauchen weiterhin regelmäßig Vielfache von 5 auf. Mathematiker sagen, dass die Menge, die alle Vielfachen von 5 enthält, den Bruchteil eines Fünftels aller ganzen Zahlen hat.
Im Gegensatz dazu gibt es zwar unendlich viele Primzahlen, aber mit zunehmender Zahl werden sie so selten, dass die Menge aller Primzahlen keinen positiven Bruchteil der ganzen Zahlen enthält, oder anders ausgedrückt, keine positive Dichte hat . Die Primzahlen sollen stattdessen die Dichte Null haben.
Szemerédi suchte nach Beispielen für sogenannte arithmetische Progressionen oder Ketten von gleichmäßig verteilten Zahlen. Stellen Sie sich zum Beispiel vor, Sie haben eine unendliche Folge von Zahlen wie die perfekten Quadrate: {1, 4, 9, 16, 25, 36, 49, 64, 81, 100, …}. Die perfekten Quadrate haben eine arithmetische Folge der Länge drei, die sich in den ersten Termen versteckt: {1, 25, 49}. Jede Zahl in dieser Progression ist 24 mehr als ihre Vorgängerin.
Szemerédi bewies, dass jede Menge, die einen positiven Bruchteil der ganzen Zahlen umfasst, beliebig lange arithmetische Folgen enthalten muss. Das Ergebnis war ein Meilenstein auf dem Teilgebiet der Mathematik, das als additive Kombinatorik bezeichnet wird.
Szémeredis Beweis war zwar brillant, aber fast unmöglich nachzuvollziehen. „Ich glaube, bis heute gibt es vielleicht nur drei oder vier Leute, die [Szemerédis] Beweis wirklich verstehen“, sagte er Terence tao, Mathematiker an der University of California, Los Angeles.
Daher war Fürstenbergs nachvollziehbarere Argumentation willkommen. Um es zu schreiben, stützte sich Fürstenberg auf Methoden aus seinem eigenen Gebiet der Mathematik, dynamische Systeme. Ein dynamisches System ist jeder Prozess, der sich mit der Zeit ändert. Das könnte etwas so Einfaches sein wie eine Billardkugel, die um einen Billardtisch rollt. Alles, was Sie brauchen, ist eine Möglichkeit, Ihr System mathematisch darzustellen, und eine Regel dafür, wie es sich entwickelt. Ein Ball kann beispielsweise durch seine Position und Geschwindigkeit beschrieben werden. Dieses System schreitet im Laufe der Zeit auf eine vorgeschriebene Weise fort und folgt den Gesetzen der klassischen Physik.
Fürstenberg interessierte sich am meisten für etwas, das man Ergodentheorie nennt. Anstatt den Zustand eines Systems zu einem bestimmten Zeitpunkt zu betrachten, untersuchen Ergodentheoretiker Statistiken über lange Zeiträume. Für eine Billardkugel könnte das bedeuten, herauszufinden, ob die Kugel aufgrund der Art und Weise, wie sie dazu neigt, von den Wänden abzuprallen, häufiger an einigen Stellen auf dem Tisch landet als an anderen.
Fürstenbergs Schlüsselidee war es, ganze Zahlenmengen nicht als feste Objekte, sondern als momentane Zustände in einem dynamischen System zu betrachten. Es mag wie ein kleiner Perspektivwechsel erscheinen, aber es erlaubte ihm, Werkzeuge aus der Ergodentheorie zu verwenden, um Ergebnisse in der Kombinatorik zu beweisen. Damals ahnte Fürstenberg noch nicht, dass seine Ideen ein Eigenleben entwickeln würden. „Es war nur so, dass ich diesen anderen Beweis gerne hatte“, sagte er. Aber andere sahen das Versprechen der Verbindung zwischen Ergodentheorie und Kombinatorik. „Eine ganze Generation von Ergodentheoretikern fing an, sich in die Kombinatorik zu stürzen und all diese Probleme zu lösen, und umgekehrt“, sagte Tao.
In den letzten Jahren haben vier Mathematiker – Bryna Kra, Joël Moreira, Florian Richter und Donald Robertson – haben Furstenbergs Techniken entwickelt, um nicht nur willkürlich lange Progressionen innerhalb einer beliebigen Menge zu finden, die einen positiven Bruchteil der ganzen Zahlen enthält, sondern unendliche Versionen von Strukturen, die Summenmengen genannt werden.
„Summensätze sind viel weniger spezifisch als Progressionen; Sie sehen viel weniger besonders aus“, sagte Robertson. „Aber es ist interessanter und heikler, weil Summen unendliche Konfigurationen sind, während Progressionen endlich sind.“
Wenn Fürstenberg eine Brücke zwischen Ergodentheorie und Kombinatorik geschlagen hat, haben Kra, Moreira, Richter und Robertson sie zu „einer sechsspurigen Autobahn“ ausgebaut, sagte Tao.
B + C Vermutung
Der Satz von Szemerédi wurde erstmals 1936 von zwei Mathematikern vorgeschlagen, aber nicht bewiesen. Einer von ihnen war ein ungarischer Mathematiker, der für seine Vermutungen berühmt war: Paul Erdős. 2016, als Moreira an seiner Doktorarbeit an der Ohio State University arbeitete, stieß er darauf eine weitere Vermutung, die Erdős aufgestellt hatte über die Strukturen, die Summenmengen genannt werden.
Eine Summenmenge wird aus zwei anderen Mengen gebildet; nenne die B und C. Die Summe, geschrieben als B + C, wird gebildet, indem alle möglichen Zahlenpaare addiert werden, wobei eine Zahl von genommen wird B und der andere aus C. Erdős vermutete dies für jede Menge A die einen positiven Bruch ganzer Zahlen enthält, gibt es andere unendliche Mengen B und C dessen Summe darin enthalten ist A. In der Arbeit, die Moreira las, hatten die Autoren die Vermutung von Erdős bewiesen, wenn A einen großen Bruchteil der ganzen Zahlen enthält. Aber für kleinere Sätze mit positiver Dichte war das Ergebnis noch unbekannt. „Sobald ich die Erklärung gelesen habe, dachte ich, dass es eine wirklich gute Frage ist, weil sie so einfach ist“, sagte Moreira. „Entweder ist es falsch, oder es sollte nicht schwierig sein. Was natürlich falsch war. Es war weder falsch noch einfach.“
Moreira brachte Richter und Robertson, Freunde von der Graduiertenschule, in das Projekt ein. Robertson, jetzt an der University of Manchester, hatte ein Jahr vor Moreira seinen Abschluss gemacht, und Richter war ein paar Jahre im Rückstand. Alle drei waren sehr versiert in der Anwendung ergodischer Theorietechniken auf die Kombinatorik. Doch dieses Problem stellte uns vor neue Herausforderungen.
„Es gab praktisch keinen Präzedenzfall dafür, unendliche Summen in einem Satz positiver Dichte zu finden“, sagte er Daniel Glascock, ein Mathematiker an der University of Massachusetts, Lowell, der die Graduiertenschule bei Moreira, Richter und Robertson besuchte.
Vielleicht aus diesem Grund erwies sich das Summenmengenproblem als schwierig zu lösen. „Wir müssen die ergodische Theorie ein bisschen erzwingen, damit sie durchkommt“, sagte Moreira. Ihre Bemühungen zahlten sich schließlich aus, und in was Marcin Sabok von der McGill University als „erstaunliche Leistung“ bezeichnet, gelang es ihnen, die Vermutung von Erdős im Jahr 2018 zu beweisen. Ihr Beweis erfolgte später veröffentlicht im Annalen der Mathematik, eine der renommiertesten Fachzeitschriften für Mathematik.
Die neuen Beweise
Dieses Papier ließ zwei große Fragen offen. Eine davon war eine andere Summenvermutung von Erdős namens the B + B + t Vermutung.
Moreira, Richter und Robertson hatten sich auch eine eigene Frage ausgedacht: Wenn Sie eine Menge mit positiver Dichte haben A, kannst du drei unendliche Mengen finden – B, C und nun D - woher B + C + D ist drinnen A? Was ist mit vier unendlichen Mengen? Fünf?
Nachdem sie die Multi-Set-Version aufgestellt hatten, steckten die Mathematiker eine Zeit lang fest. Es schien, dass die Techniken, die sie für die Zweimengen-Vermutung verwendet hatten, ihre Grenzen erreicht hatten.
„Wir konnten keine dynamische Umformulierung dieses Problems finden“, sagte Richter. Ihr Ansatz, sagte er, sei „einfach am Anfang gescheitert“.
Zwei Jahre vergingen, bevor sie wirkliche Fortschritte sahen. Zu diesem Zeitpunkt war Richter Postdoktorand an der Northwestern University, wo er Bryna Kra war Professorin. Im Jahr 2020, das durch die Covid-19-Pandemie daran gehindert wurde, sich persönlich zu treffen, diskutierten Kra und Richter das Summenproblem über Zoom.
„Schließlich kamen wir auf einige andere Variationen, die wir verstanden“, sagte Kra.
Kra und Richter begannen jede Woche mit Moreira und Robertson zu sprechen und überprüften den Beweis von 2018 erneut.
„Wir mussten jeden Schritt des Beweises überdenken, beginnend mit dieser Übersetzung in ein dynamisches System“, sagte Kra.
Hilfreich für ihre Sache war ein Jahr 2019 Krepppapier von einem französischen Mathematiker namens Bernhard Gastgeber. Host hatte das Ergebnis von Moreira, Richter und Robertson erneut bewiesen und herausgefunden, wie man die Ergodentheorie zum Klingen bringt. Nach Meinung von Moreira hat Host „gesehen, wie wir unseren Beweis so schreiben, wie er hätte geschrieben werden sollen.“
Mit den Verbesserungen von Host in der Hand fuhren Kra, Moreira, Richter und Robertson fort, ihren Beweis zu optimieren, indem sie versuchten, das einfachste und eleganteste mögliche Argument herauszuziehen. "Wir haben es nur seziert, denke ich, immer und immer wieder, um wirklich zu sehen: Was ist der Kern des Problems?" sagte Richter. „Am Ende hatten wir einen Beweis, der sehr wenig Ähnlichkeit mit dem ursprünglichen Beweis hatte.“
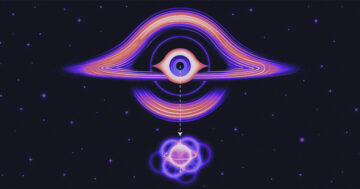
Der Beweis, mit dem sie endeten, betrachtete wie der von Fürstenberg die unendlichen Mengen ganzer Zahlen als Zeitstempel in einem dynamischen System. Dieses dynamische System stellt man sich jedoch besser als Punkte vor, die im Raum herumspringen.
Hier ist ein grobes Bild davon, wie es funktioniert: Beginnen Sie, indem Sie in einer Ecke eines geschlossenen Raums stehen, nennen Sie es Ecke 0. Sie sind mit einer Liste von Zeiten ausgestattet A. Dieser Satz, A, ist eine Menge von ganzen Zahlen mit positiver Dichte.
Sie sind auch mit einer Regel ausgestattet, um sich im Raum zu bewegen. Jede Sekunde bewegst du dich an eine neue Stelle, basierend darauf, wo du gerade gestanden hast. Die genaue Regel, die Sie befolgen, wird so gestaltet, dass sie zu Ihren Zeiten passt A — immer wenn der Zeitstempel drin ist A, finden Sie sich in einem speziellen Bereich des Raums wieder.
Sag zum Beispiel A besteht aus allen Zahlen, die durch 4 teilbar sind, und jede Sekunde bewegt man sich im Uhrzeigersinn in die nächste Ecke des Raums. Nach einer Sekunde bewegst du dich zu Ecke 1; nach zwei Sekunden Ecke 2 usw. Dann alle vier Schritte – also für jede Zeit, die drin ist EIN - Sie sind zur ursprünglichen Ecke 0 zurückgekehrt.
Dieser Prozess geht ewig weiter. Wenn Sie im Uhrzeigersinn von Ecke zu Ecke reisen, besuchen Sie jede Ecke unendlich oft. Ein Punkt, dem man unendlich oft nahe kommt, wird als Häufungspunkt bezeichnet.
Kra, Moreira, Richter und Robertson haben bewiesen, dass man einen dieser Punkte geschickt auswählen kann, um seine Summenmenge zu finden B + C. Nehmen Sie im Eckenbeispiel Ecke 1. Sie kommen dort zu den Zeiten 1, 5, 9 und 13 an – Zeiten, die wie 4 aussehenn + 1 für eine ganze Zahl n. Lassen B sei die Menge jener Zeiten.
Stellen Sie sich nun vor, Sie beginnen nicht bei Ecke 0, sondern bei Ecke 1. Das bedeutet, dass Sie sich bei Zeiten, die durch 4 teilbar sind, wieder bei Ecke 1 wiederfinden und drei Schritte später bei Ecke 0 ankommen: manchmal 3, 7, 11 oder eine beliebige Zahl der Form 4n + 3. Rufen Sie die Menge dieser Zeiten auf C.
Beginnen Sie nun Ihren Prozess erneut von Ecke 0. Schauen Sie sich dieses Mal an, was passiert, wenn Sie eine Zahl von nehmen B und eine Zahl von C – sagen wir, 13 von B und 3 von C - und addiere sie.
Dies würde 13 + 3 = 16 Sekunden dauern. Da 16 ein Vielfaches von 4 ist, ist es drin A. Sie können aber auch vorhersagen, dass 13 + 3 durch 4 teilbar und damit in sein wird A, ohne tatsächlich 13 und 3 zusammenzuzählen. Verfolgen Sie einfach, was im dynamischen System passiert, wenn Sie 13 + 3 Sekunden warten: Zuerst vergehen 13 Sekunden. An diesem Punkt befinden Sie sich in Ecke 1. Dann gehen Sie, ausgehend von Ecke 1, drei weitere Schritte, was Sie zurück zu Ecke 0 bringt. Da Sie bei Ecke 0 gestartet und dort wieder gelandet sind, müssen Sie auf a gewartet haben ein Vielfaches von vier Sekunden, was bedeutet, dass die Gesamtzeit im ursprünglichen Satz eine Zahl war A.
Damit dieses Argument funktioniert, musste sich die Gruppe mit vielen kniffligen mathematischen Details auseinandersetzen. Zum Beispiel stehen Ihnen in den meisten Fällen unendlich viele Stellen zur Verfügung, an die Sie sich bewegen können, nicht nur vier Ecken. Das bedeutet, dass Sie nicht unendlich oft an eine Stelle zurückkehren; du wirst ihm nur unendlich oft nahe kommen. Das führte neue mathematische Komplikationen in das Argument ein. Aber sobald sie herausgefunden hatten, wie der Prozess funktionieren würde, wussten sie, dass sie in der Lage sein würden, die schwierigeren Fragen anzugehen, denen sie nachgingen.
„Wir haben diesen Beweis hier gefunden, und es war sofort klar, wie man ihn verallgemeinern kann“, sagte Richter, der jetzt an der Eidgenössischen Technischen Hochschule Lausanne ist. Um beispielsweise die Multi-Set-Version der Vermutung zu beweisen, könnten die Forscher dem Pfad einfach einen Häufungspunkt hinzufügen. Das Gesamtargument war das gleiche, nur mit einer neuen Komplikationsebene.
Es war nicht einfach, alle technischen Einzelheiten herauszuarbeiten. Nachdem sie sich für ihren dynamischen Aufbau entschieden hatten, brauchten Kra, Moreira, Richter und Robertson über ein Jahr, um Beweise für die schwierigeren Vermutungen zu erarbeiten. Im Juni dieses Jahres veröffentlichte die Gruppe schließlich zwei Papiere. Einer bewies die Multi-Set-Version der Sumset-Vermutung. Die andere bewies die B + B + t Version der Vermutung, die erfordert, dass der zweite Satz C gleich dem ersten Satz sein B, verschoben um eine Konstante, t.
Nächste Schritte
Obwohl die Juni-Papiere zwei Fragen zu Summensätzen lösen, sehen Kra, Moreira, Richter und Robertson eine lange Zukunft für ihre Forschungsrichtung. „Wie bei allem, was Erdős verlangt, möchte er nur, dass wir unseren Fuß in die Tür setzen“, sagte Moreira, jetzt an der University of Warwick. „Aber jetzt müssen wir die Tür öffnen und erkunden, was es sonst noch gibt.“
In ihren neuen Arbeiten skizzieren die vier Mathematiker mehrere mögliche Forschungsrichtungen in Form von noch unbeantworteten Fragen. Man verlässt sich darauf, dass zwar jede Menge positiver Dichte A enthält eine unendliche Summe B + C, enthält es nicht unbedingt die beiden Komponenten B und C. Wann können Sie darauf bestehen B und C muss auch drin sein A? Die Autoren fordern Mathematiker auch heraus, herauszufinden, ob sie eine unendliche Folge von unendlichen Mengen finden können, deren Summen enthalten sind A.
Eine weitere offene Frage in diesem Bereich wurde bereits von Matt Bowen, einem Doktoranden von Sabok an der McGill University, beantwortet. Im Oktober hat er gepostet ein Beweis dafür, dass man eine Summe finden kann, wenn man jeder Ganzzahl eine von wenigen Farben zuweist B + C und ein Produkt von Mengen BC innerhalb nur einer der Farben.
Wo genau das neue Werk von Kra, Moreira, Richter und Robertson noch hinführen wird, ist noch nicht bekannt. Aber zumindest Tao ist optimistisch in Bezug auf die neuen Techniken, die die Gruppe entwickelt hat. Was sie mit ihren Methoden erreichen, sei „eigentlich ganz erstaunlich“, sagte er. „Es gibt andere Fragen, die unendliche Mengen betreffen, die zuvor als hoffnungslos galten und jetzt in Reichweite sind.“