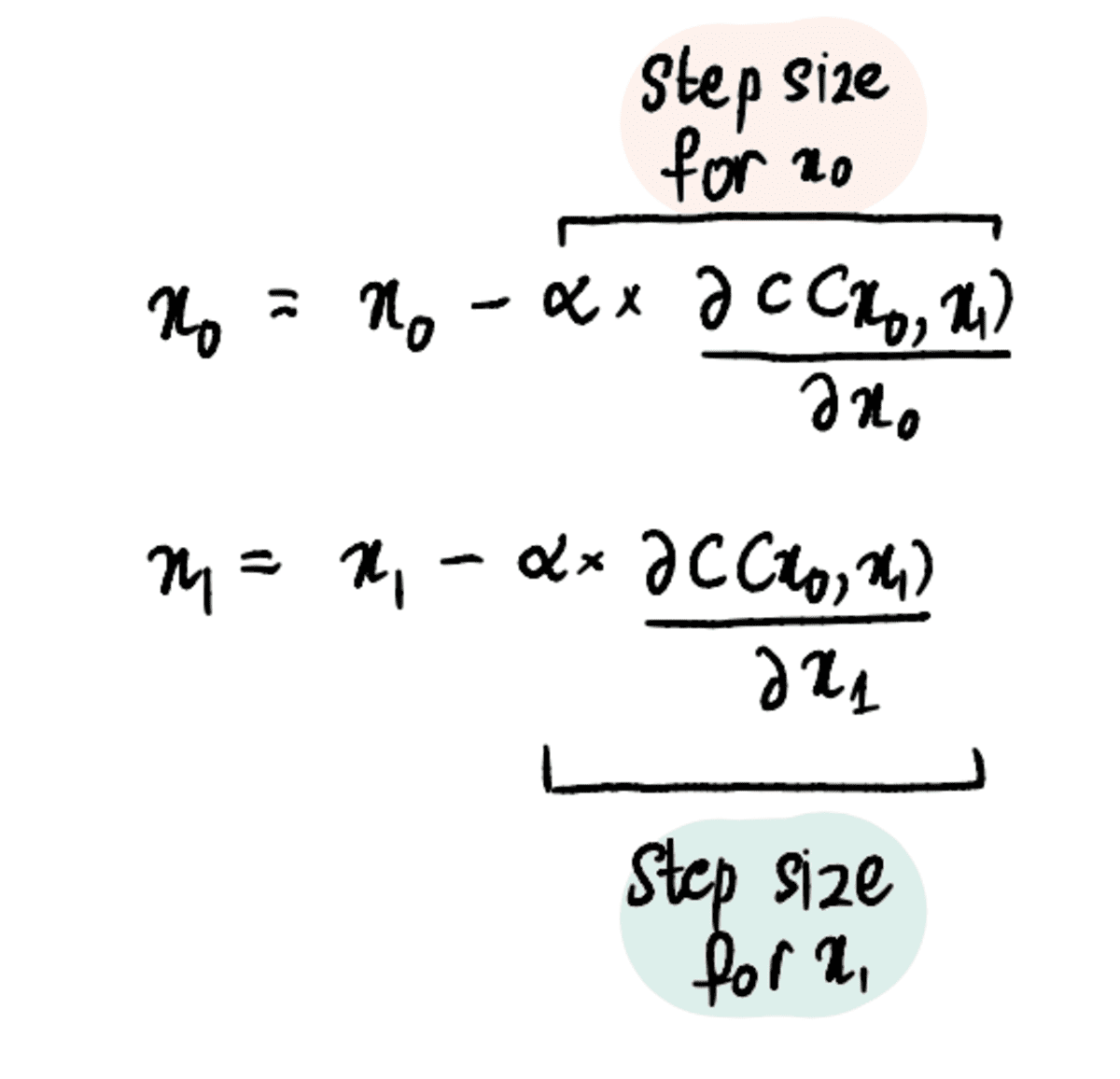Tagasi põhitõdede juurde, osa Dos: Gradient Descent

Tere tulemast meie teise osasse Tagasi põhitõdede juurde seeria. Aastal esimene osa, käsitlesime, kuidas kasutada lineaarset regressiooni ja kulufunktsiooni, et leida meie majahindade andmete jaoks kõige sobivam rida. Siiski nägime ka seda testimist mitu korda pealtkuulamiseks väärtused võivad olla tüütud ja ebaefektiivsed. Selles teises osas uurime põhjalikumalt Gradient Descenti – võimsat tehnikat, mis aitab meil leida täiusliku. pealtkuulamiseks ja optimeerida meie mudelit. Uurime selle taga olevat matemaatikat ja vaatame, kuidas seda meie lineaarse regressiooni probleemi puhul rakendada.

Gradiendi laskumine on võimas optimeerimisalgoritm, mis eesmärk on kiiresti ja tõhusalt leida kõvera miinimumpunkt. Parim viis selle protsessi visualiseerimiseks on kujutada ette, et seisate mäe otsas ja orus ootab teid kullaga täidetud aardekirst.

 

 

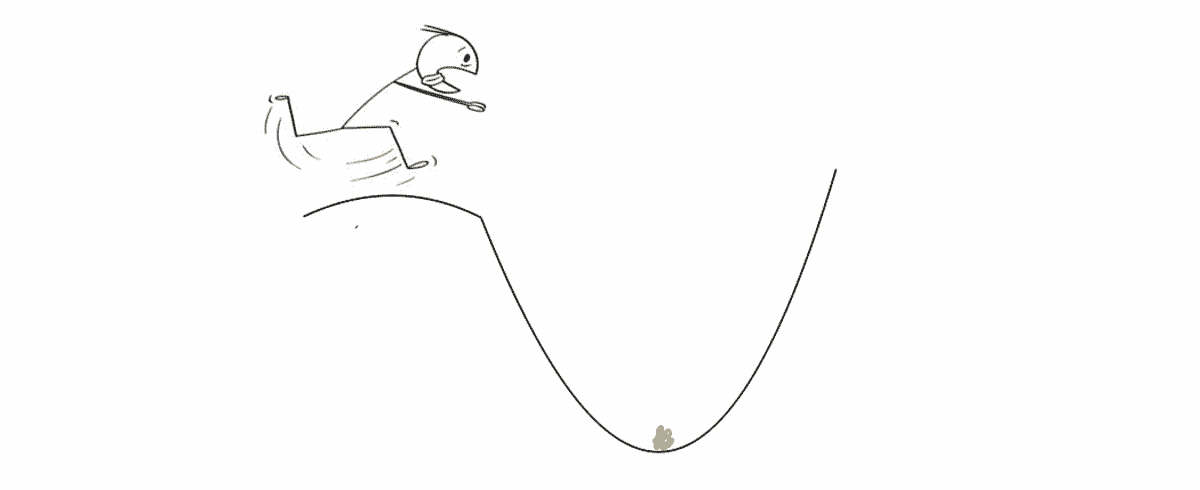
Oru täpne asukoht on aga teadmata, sest väljas on ülipime ja midagi pole näha. Veelgi enam, soovite jõuda orgu enne, kui keegi teine ​​seda teeb (sest soovite kogu varanduse endale). Kallakuga laskumine aitab teil maastikul navigeerida ja selleni jõuda optimaalselt punkt tõhusalt ja kiiresti. Igas punktis ütleb see teile, kui palju samme teha ja millises suunas peate neid tegema.

Samamoodi saab gradiendi laskumist rakendada meie lineaarse regressiooni probleemile, kasutades algoritmi sätestatud samme. Et visualiseerida miinimumi leidmise protsessi, joonistame graafiku MSE kõver. Me juba teame, et kõvera võrrand on:

 

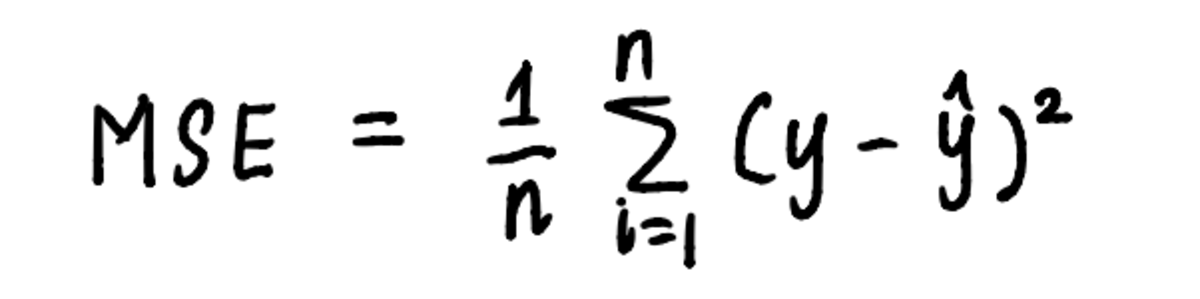
kõvera võrrand on võrrand, mida kasutatakse MSE arvutamiseks

 

Ja alates Eelmine artikkel, me teame, et võrrand MSE meie probleem on:

 

 

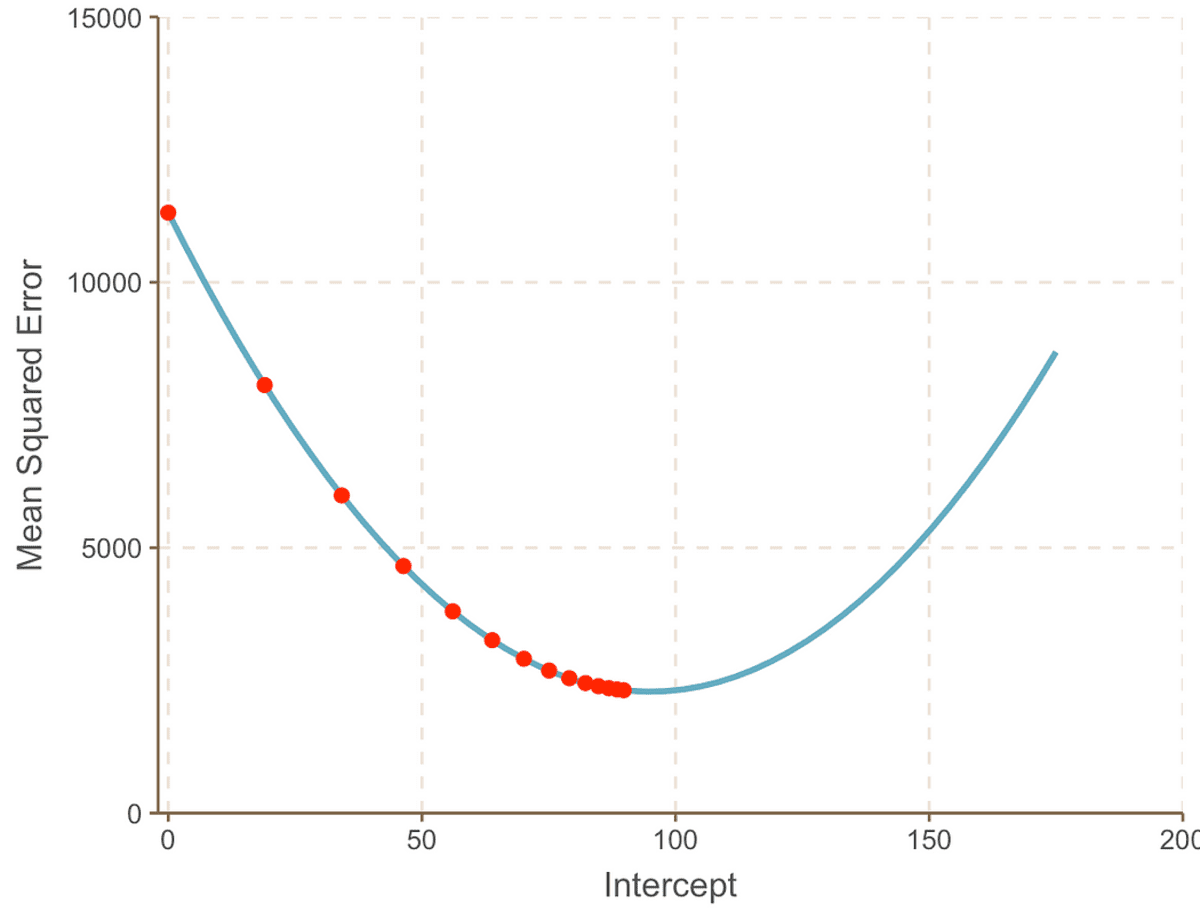
Kui me välja suumime, näeme, et an MSE kõvera (mis meenutab meie orgu) leiate, asendades hulga pealtkuulamiseks väärtused ülaltoodud võrrandis. Nii et ühendame 10,000 XNUMX väärtust pealtkuulamiseks, et saada selline kõver:

 

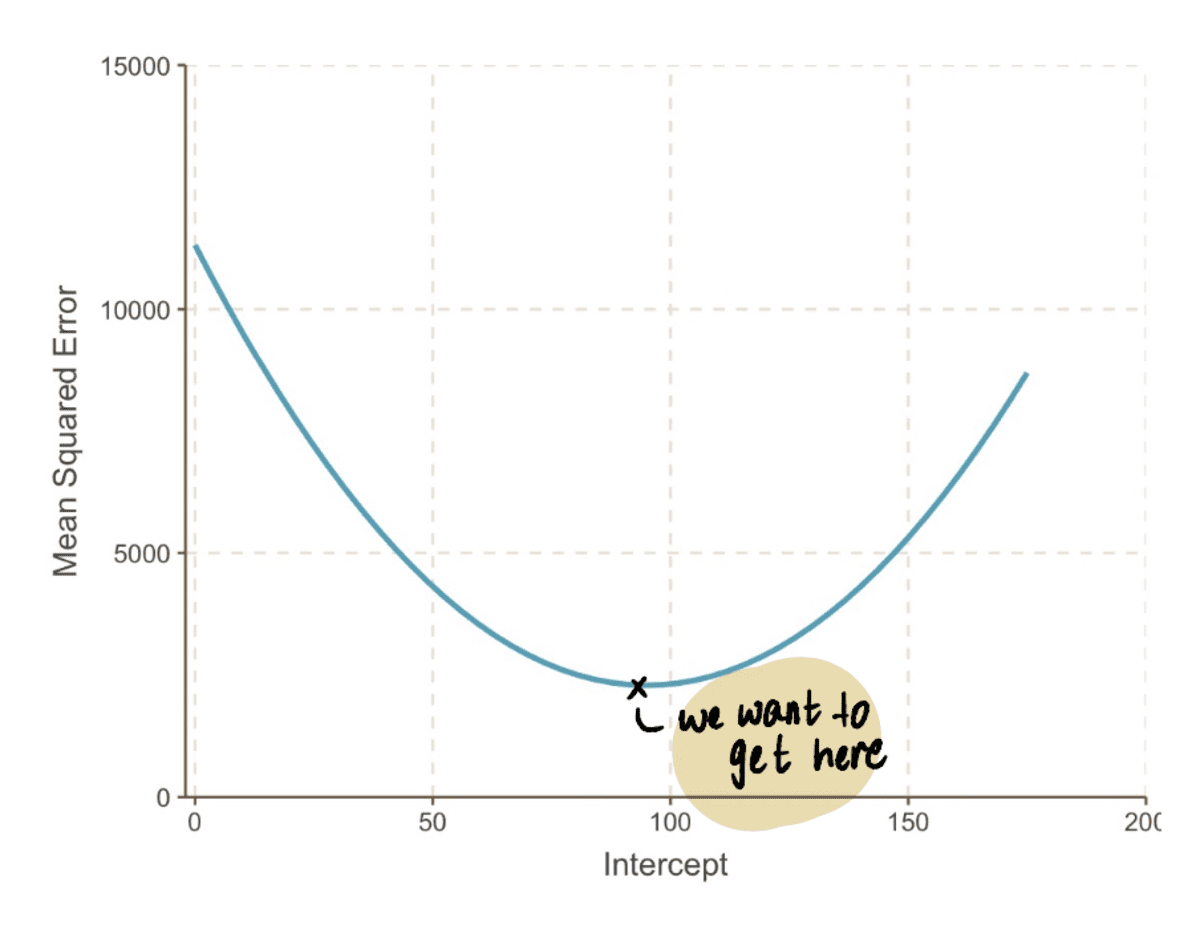
tegelikkuses me ei tea, kuidas MSE kõver välja näeb

 

Eesmärk on jõuda selle põhjani MSE kõver, mida saame teha, järgides neid samme:

1. samm: alustage lõikeväärtuse juhusliku esialgse arvamisega

Sel juhul oletame oma esialgset oletust pealtkuulamiseks väärtus on 0.

2. samm: arvutage MSE kõvera gradient selles punktis

. gradient kõvera punktis kujutab puutuja (väljamõeldud viis öelda, et joon puudutab kõverat ainult selles punktis) selles punktis. Näiteks punktis A on gradient Euroopa MSE kõverat saab esitada punase puutuja joonega, kui lõikepunkt on võrdne 0-ga.

 

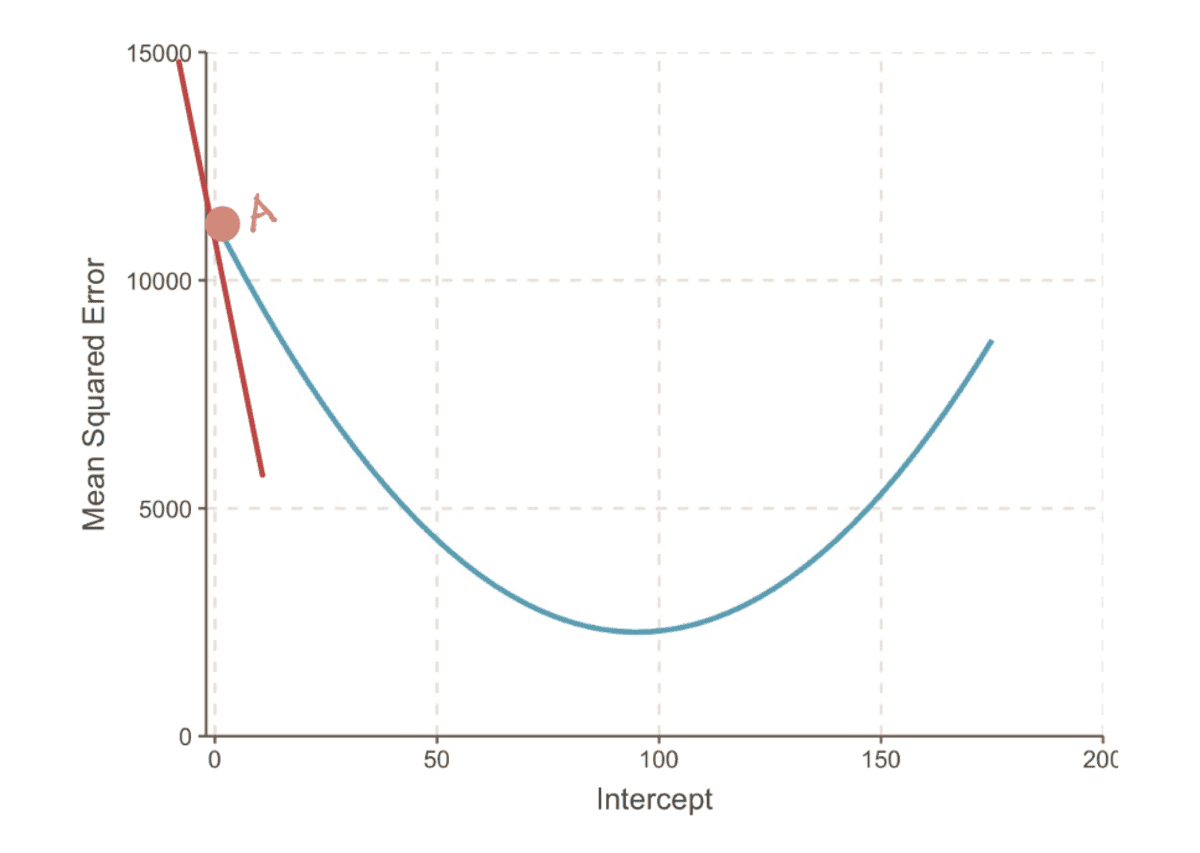
MSE kõvera gradient, kui lõikepunkt = 0

 

Selleks, et määrata väärtus gradient, rakendame oma teadmisi arvutusest. Täpsemalt, gradient on võrdne kõvera tuletisega pealtkuulamiseks antud punktis. Seda tähistatakse järgmiselt:

 

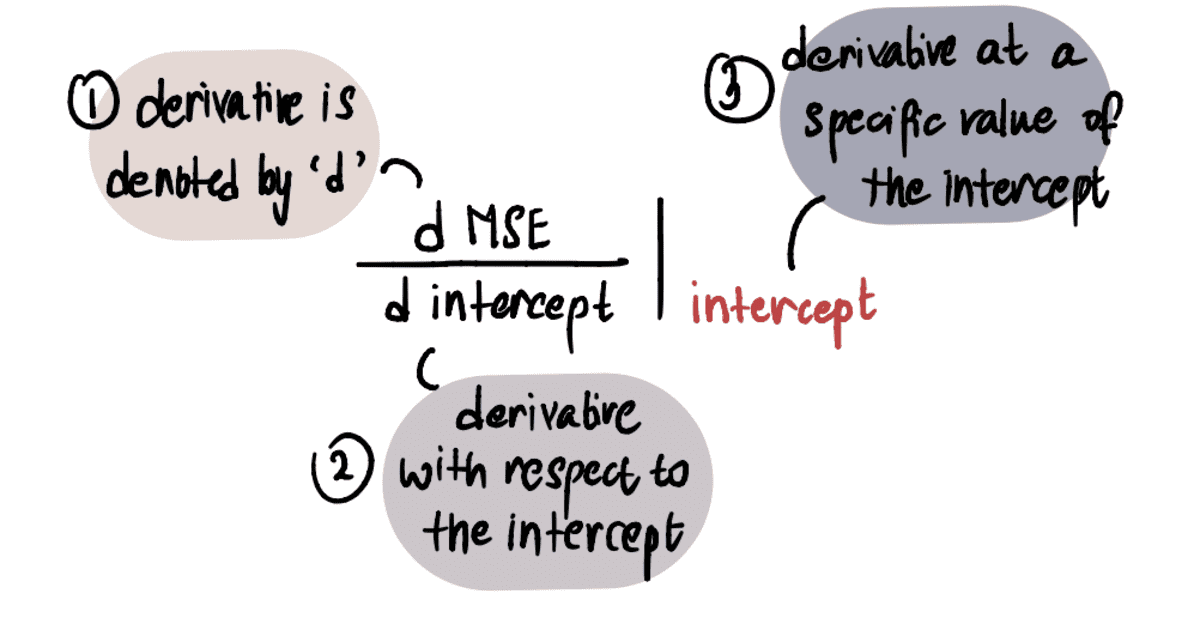
MÄRKUS. Kui te pole tuletisinstrumentidega tuttav, soovitan seda vaadata Khan Academy video kui huvitab. Vastasel juhul saate vaadata järgmist osa ja siiski jälgida ülejäänud artiklit.

Arvutame välja MSE kõvera tuletis järgmiselt:

 

 

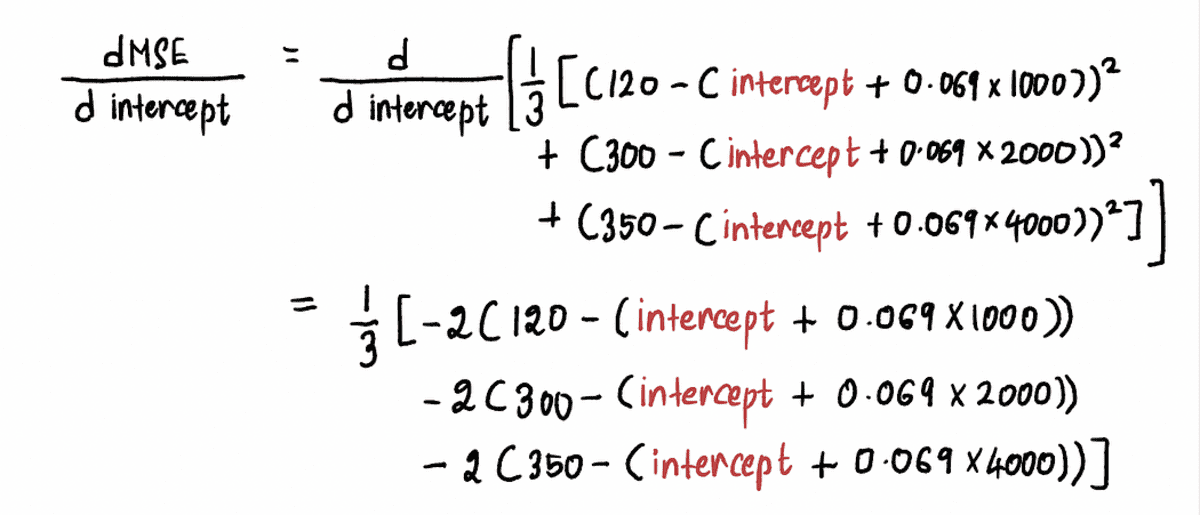
Nüüd, et leida gradient punktis A, asendame väärtuse pealtkuulamiseks punktis A ülaltoodud võrrandis. Alates pealtkuulamiseks = 0, tuletis punktis A on:

 

 

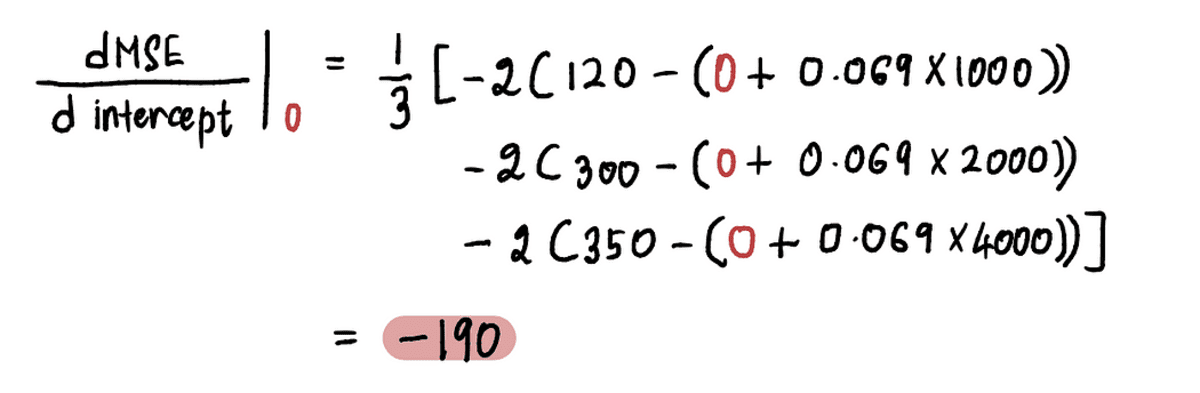
Nii et kui pealtkuulamiseks = 0, gradient = -190

MÄRKUS: Optimaalsele väärtusele lähenedes lähenevad gradiendi väärtused nullile. Optimaalse väärtuse korral on gradient võrdne nulliga. Ja vastupidi, mida kaugemal me optimaalsest väärtusest oleme, seda suuremaks muutub gradient.

 

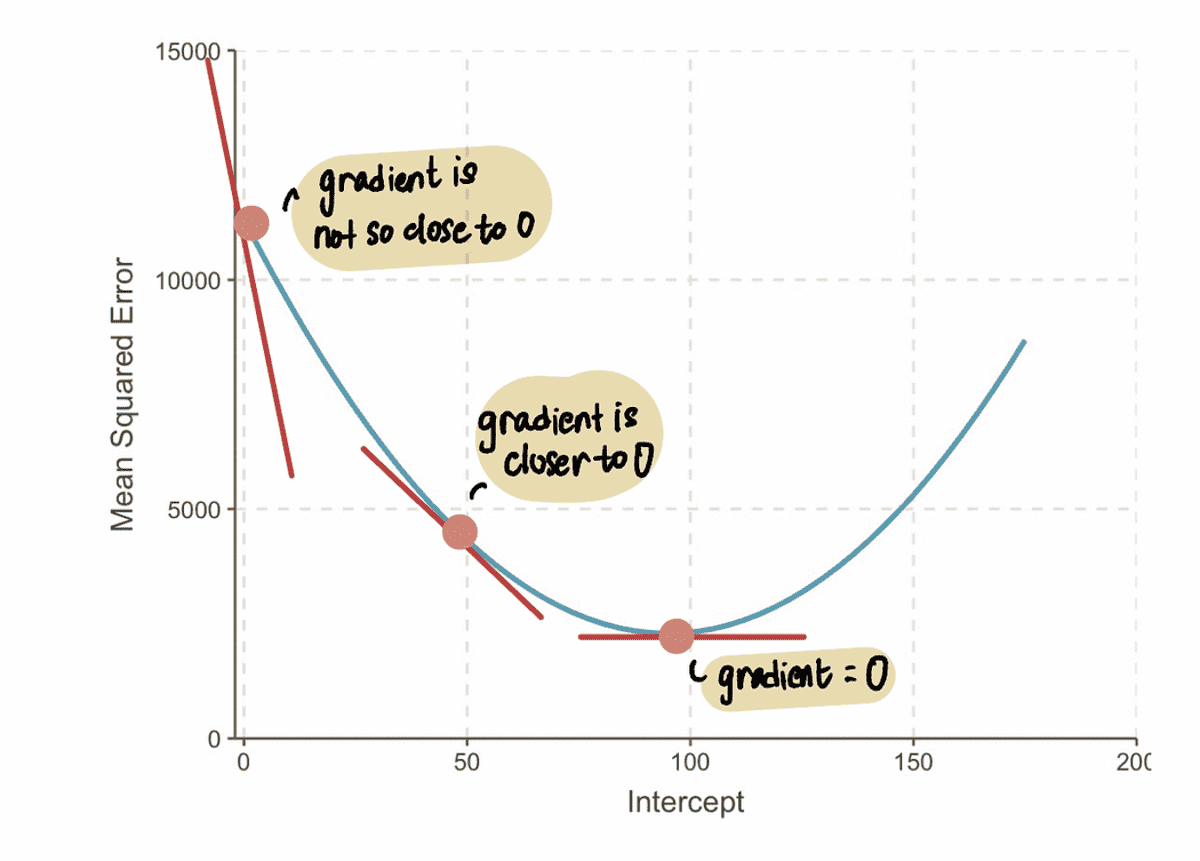
Sellest saame järeldada, et sammu suurus peaks olema seotud gradient, sest see ütleb meile, kas peaksime astuma väikese või suure sammu. See tähendab, et kui gradient kõvera väärtus on 0 lähedal, siis peaksime astuma beebisamme, sest oleme optimaalse väärtuse lähedal. Ja kui gradient on suurem, peaksime astuma suuremaid samme, et kiiremini optimaalse väärtuseni jõuda.

MÄRKUS: Kui aga astume ülisuure sammu, siis võime teha suure hüppe ja optimaalsest punktist ilma jääda. Seega peame olema ettevaatlikud.

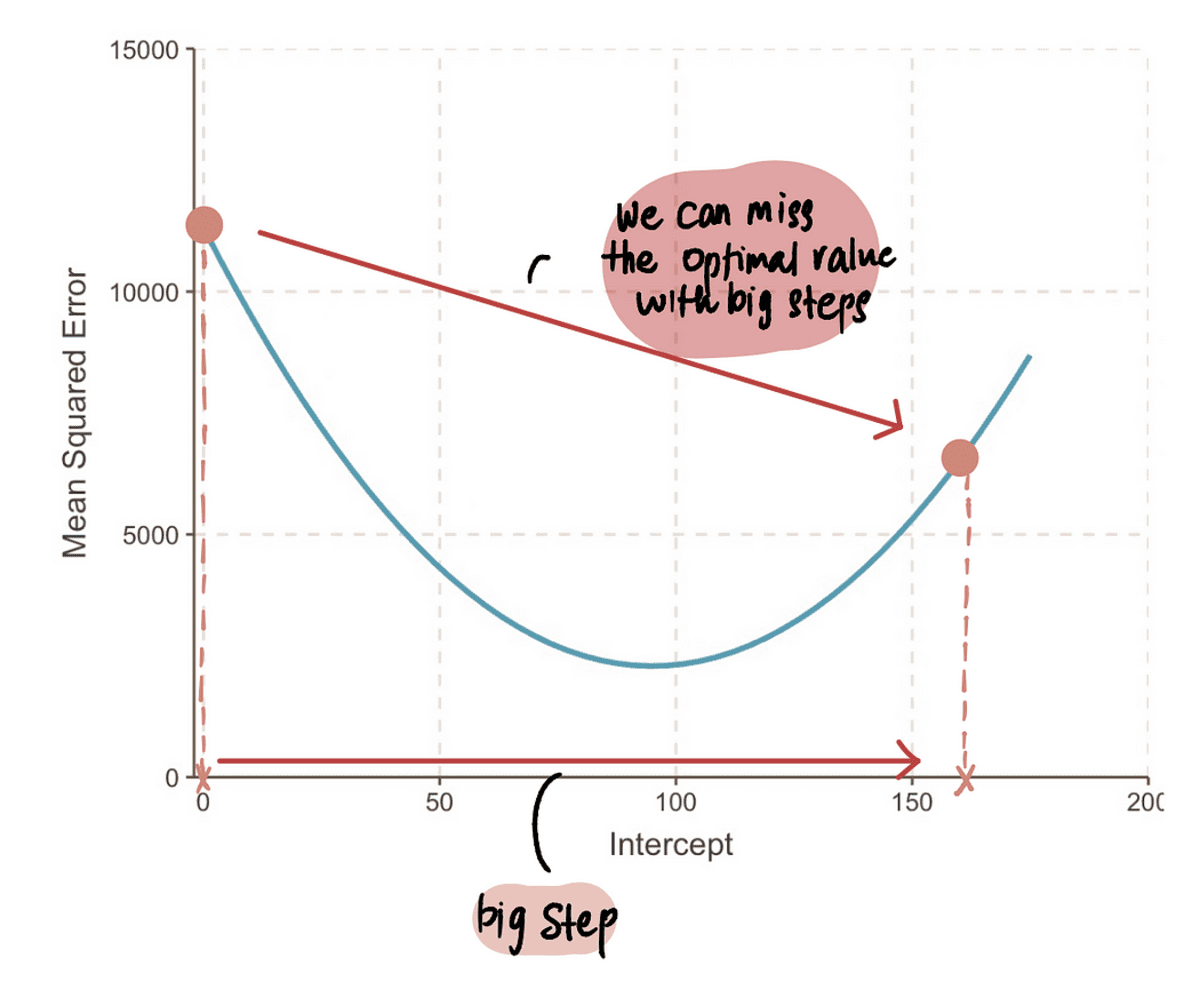
3. samm: arvutage sammu suurus gradiendi ja õppimiskiiruse abil ning värskendage lõikeväärtust

Kuna me näeme, et Sammu suurus ja gradient on üksteisega võrdelised, Sammu suurus määratakse korrutades gradient etteantud konstantse väärtusega, mida nimetatakse Õppimise määr:

 

 

. Õppimise määr kontrollib suurust Sammu suurus ja tagab, et astutud samm ei oleks liiga suur ega liiga väike.

Praktikas on õppimismäär tavaliselt väike positiivne arv, mis on ? 0.001. Kuid meie probleemi jaoks määrame selle väärtuseks 0.1.

Nii et kui lõikepunkt on 0, siis Astme suurus = gradient x Õppimise määr = -190*0.1 = -19.

Põhinedes Sammu suurus arvutasime ülal, värskendame pealtkuulamiseks (teise nimega muutke meie praegust asukohta) kasutades mõnda neist ekvivalentsetest valemitest:

 

 

Uue leidmiseks pealtkuulamiseks selles etapis ühendame asjakohased väärtused…

 

 

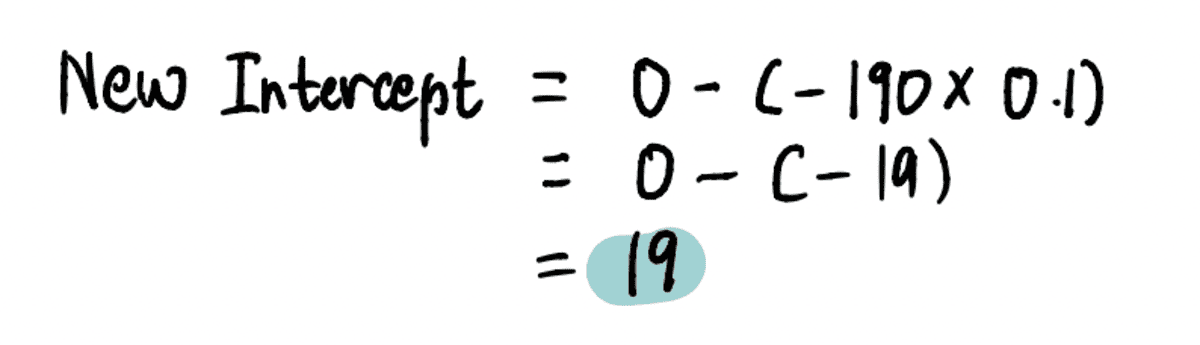
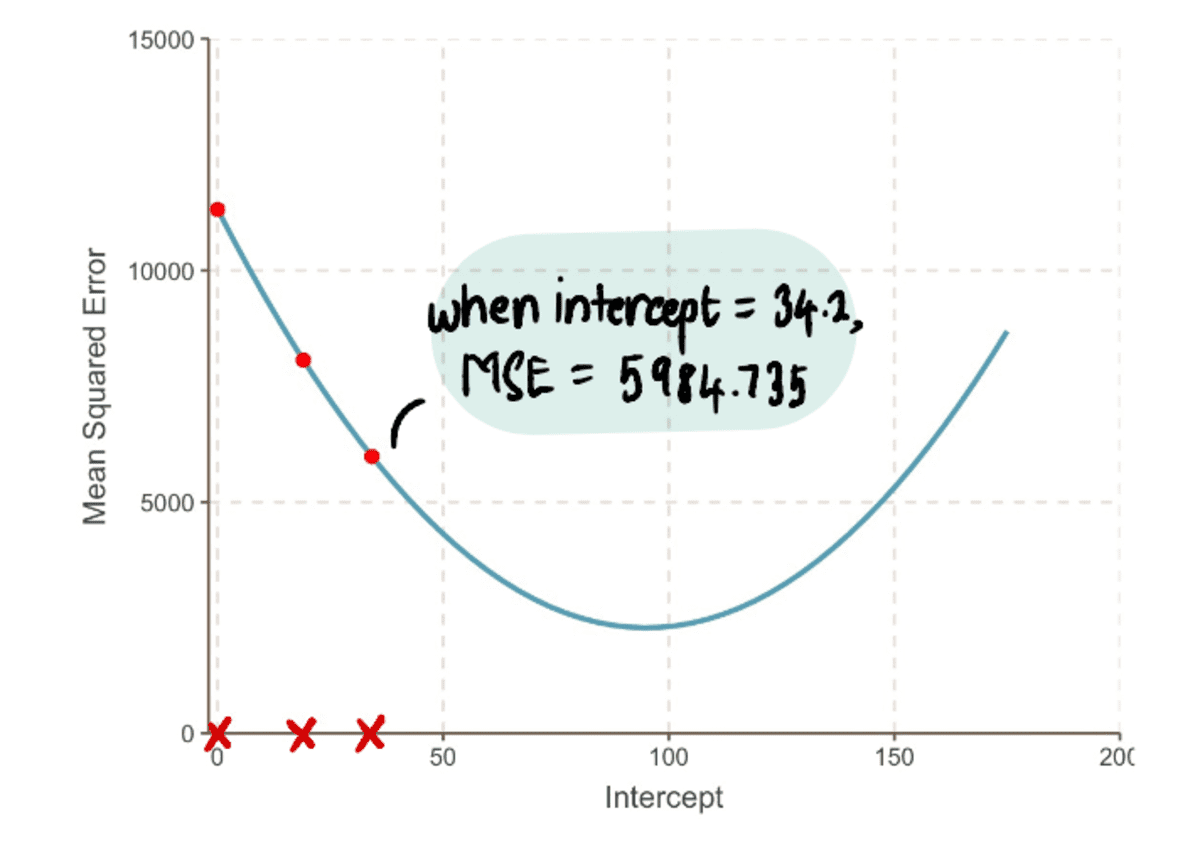
… ja leidke, et see on uus pealtkuulamiseks = 19.

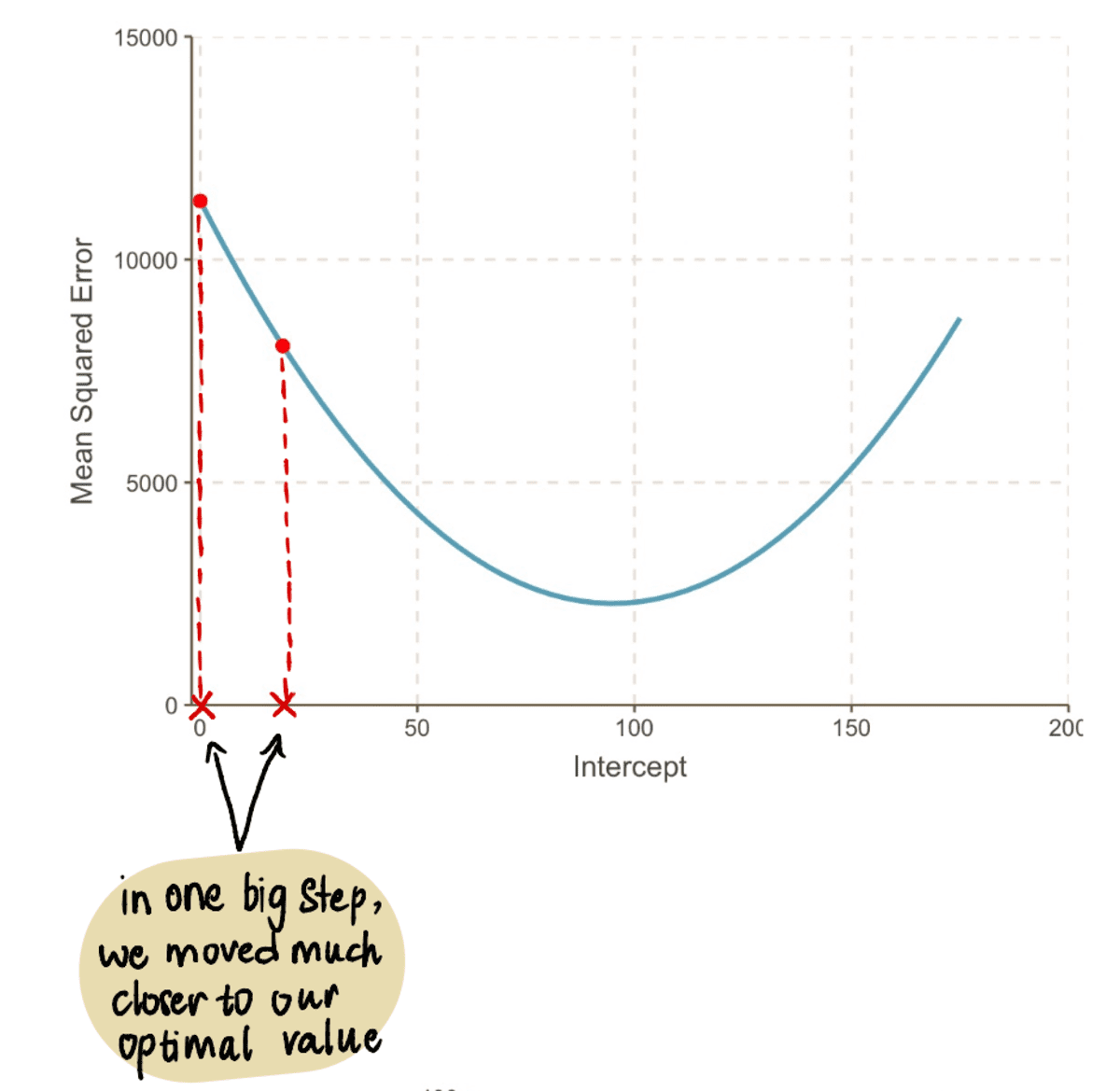
Nüüd ühendage see väärtus MSE võrrand, leiame, et MSE kui pealtkuulamiseks on 19 = 8064.095. Märkame, et ühe suure sammuga jõudsime oma optimaalsele väärtusele lähemale ja vähendasime MSE.

 

 

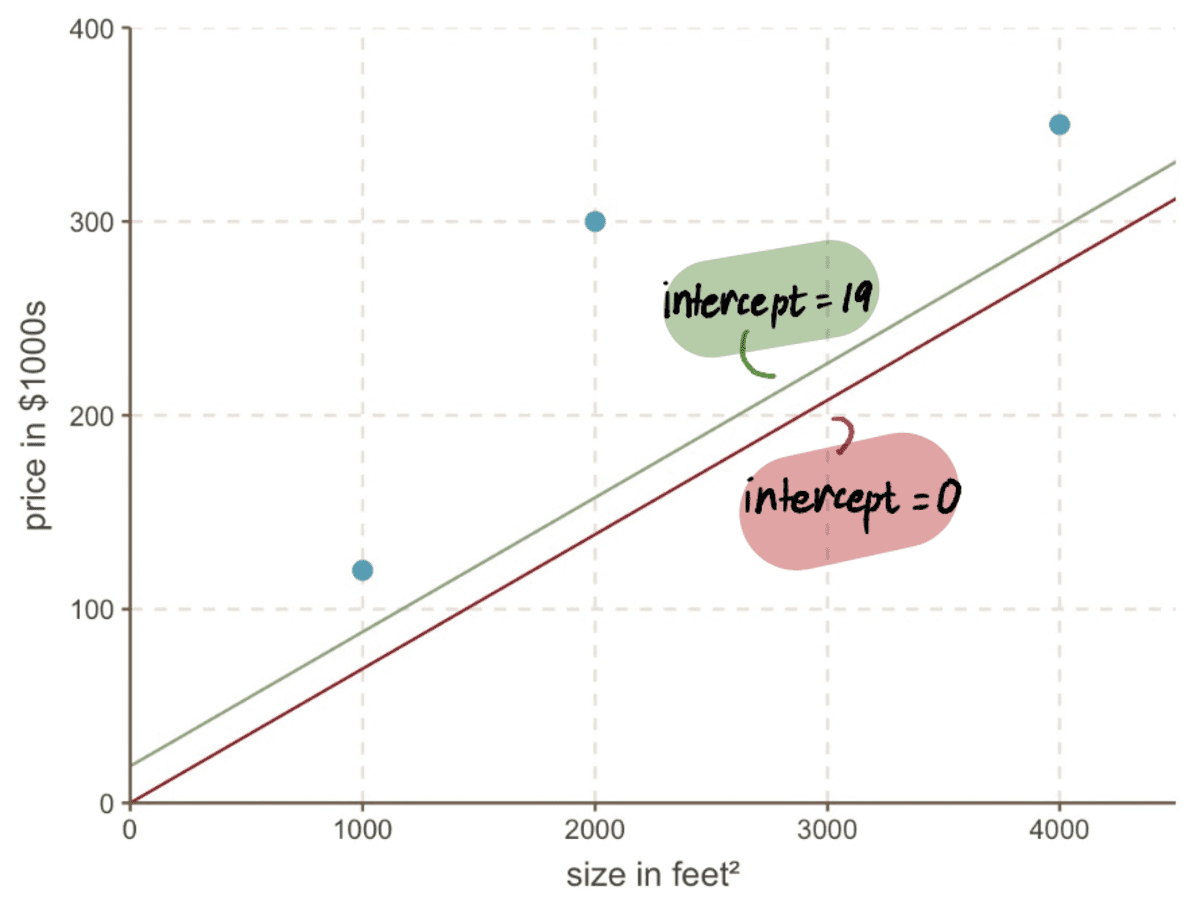
Isegi kui vaatame oma graafikut, näeme, kui palju parem on meie uus rida pealtkuulamiseks 19 sobib meie andmetega kui meie vana rida pealtkuulamiseks 0:

 

 

4. samm: korrake samme 2–3

Kordame samme 2 ja 3, kasutades värskendatud pealtkuulamiseks väärtus.

Näiteks alates uuest pealtkuulamiseks väärtus selles iteratsioonis on 19, järgmine Samm 2, arvutame gradiendi selles uues punktis:

 

 

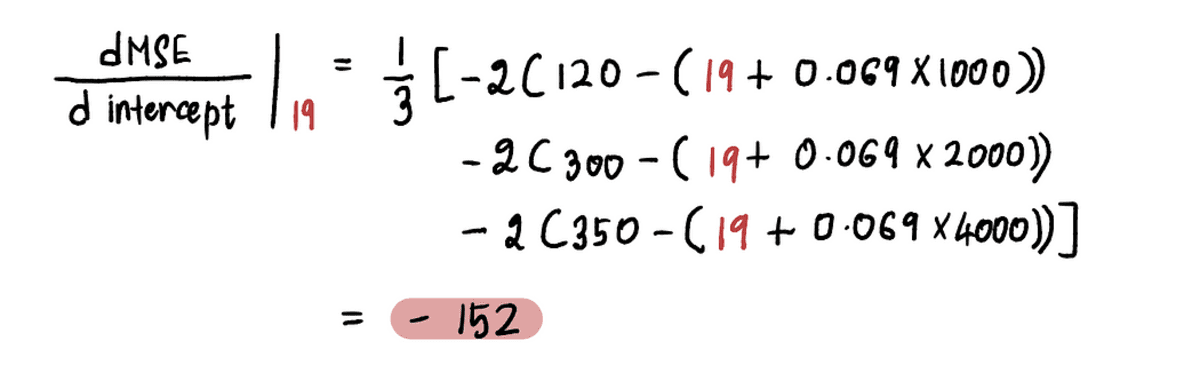
Ja me leiame, et gradient Euroopa MSE kõver lõikepunkti väärtuse 19 juures on -152 (nagu on kujutatud punase puutuja joonega alloleval joonisel).

 

 

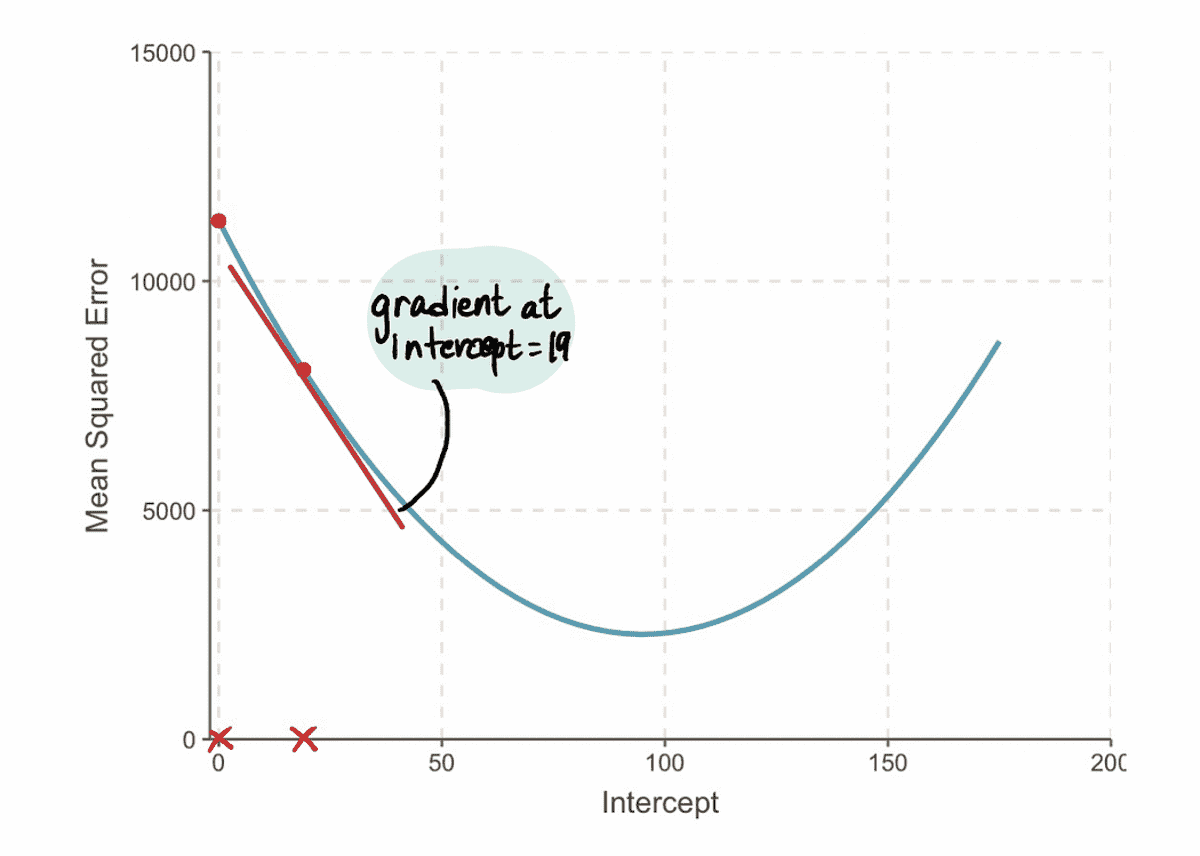
Järgmine, vastavalt Samm 3, arvutame välja Sammu suurus:

 

 

Ja seejärel värskendage pealtkuulamiseks väärtus:

 

 

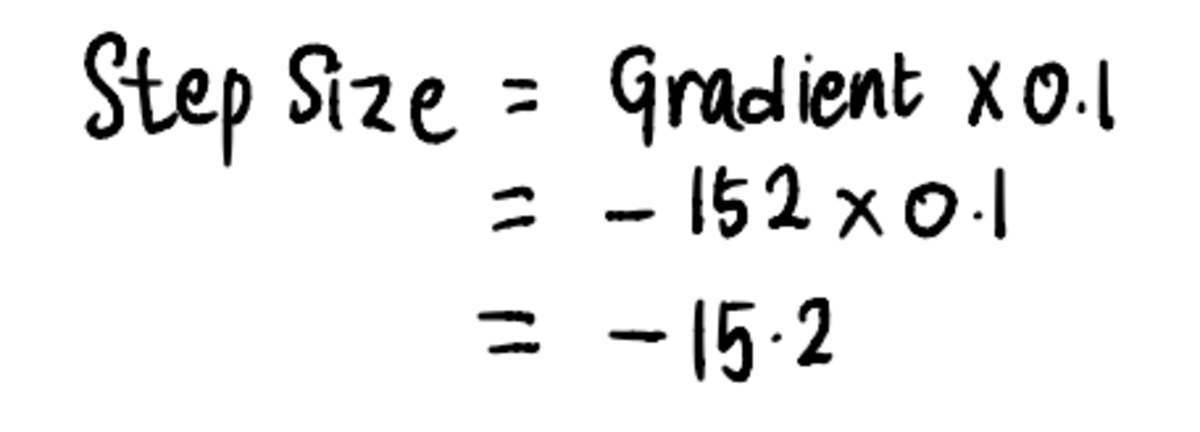
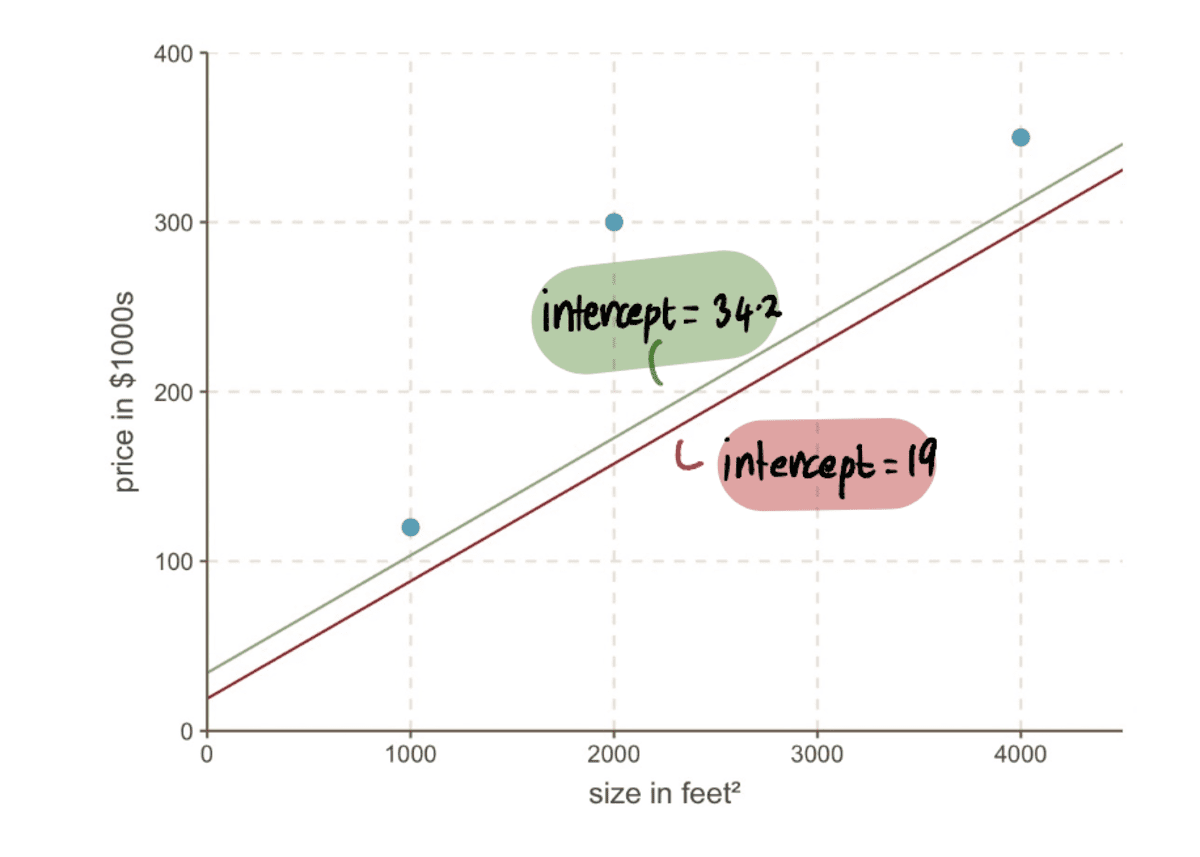
Nüüd saame võrrelda joont eelmisega pealtkuulamiseks 19-st uuele liinile uue lõikepunktiga 34.2…

 

 

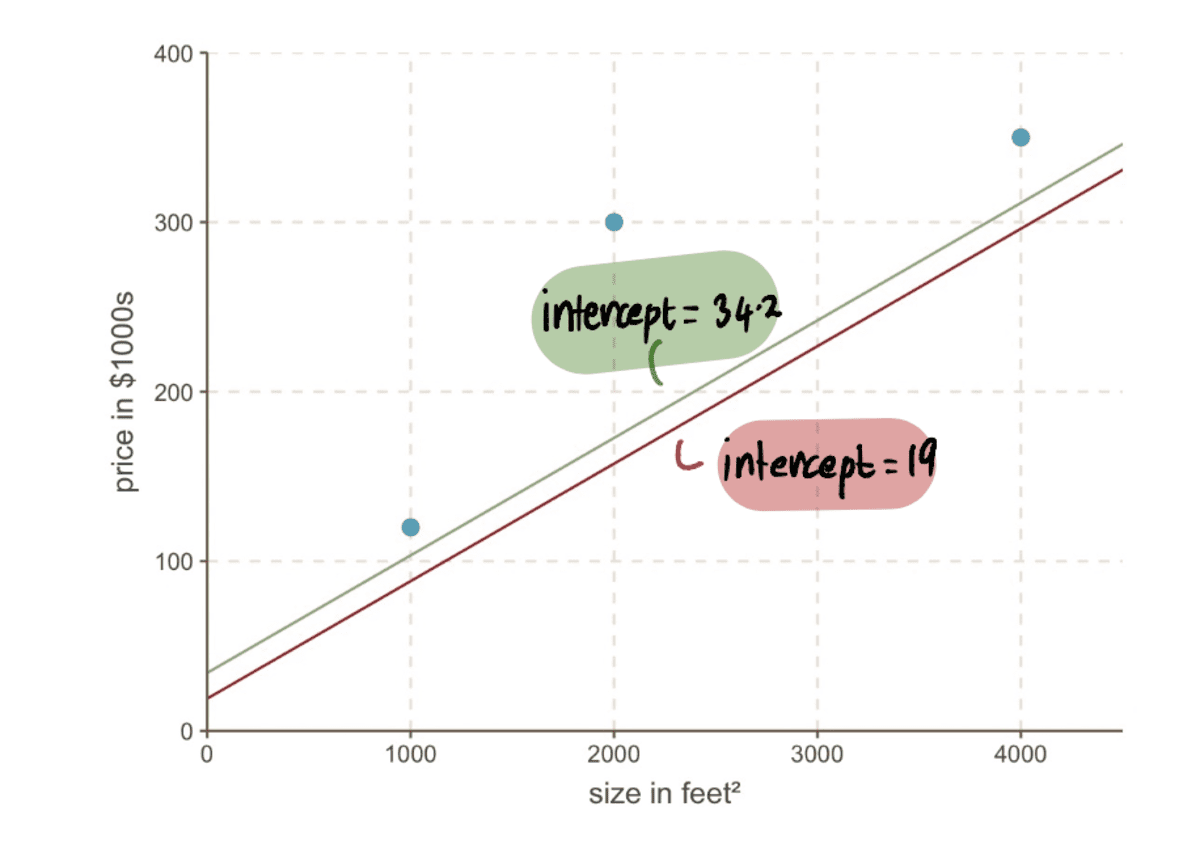
…ja näeme, et uus rida sobib andmetega paremini.

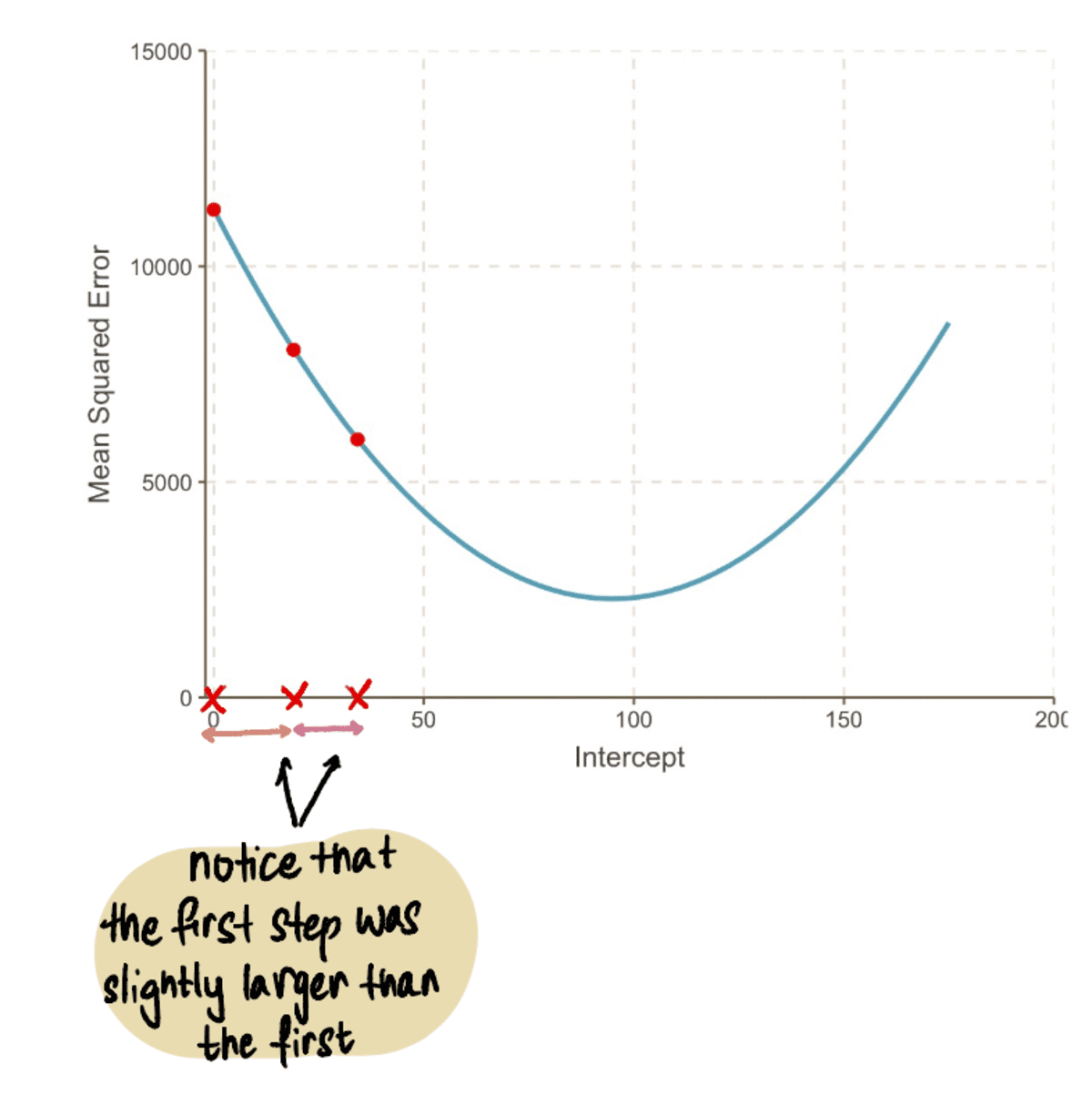
Üldiselt MSE muutub väiksemaks…

 

 

…ja meie Sammude suurused muutuvad väiksemaks:

 

 

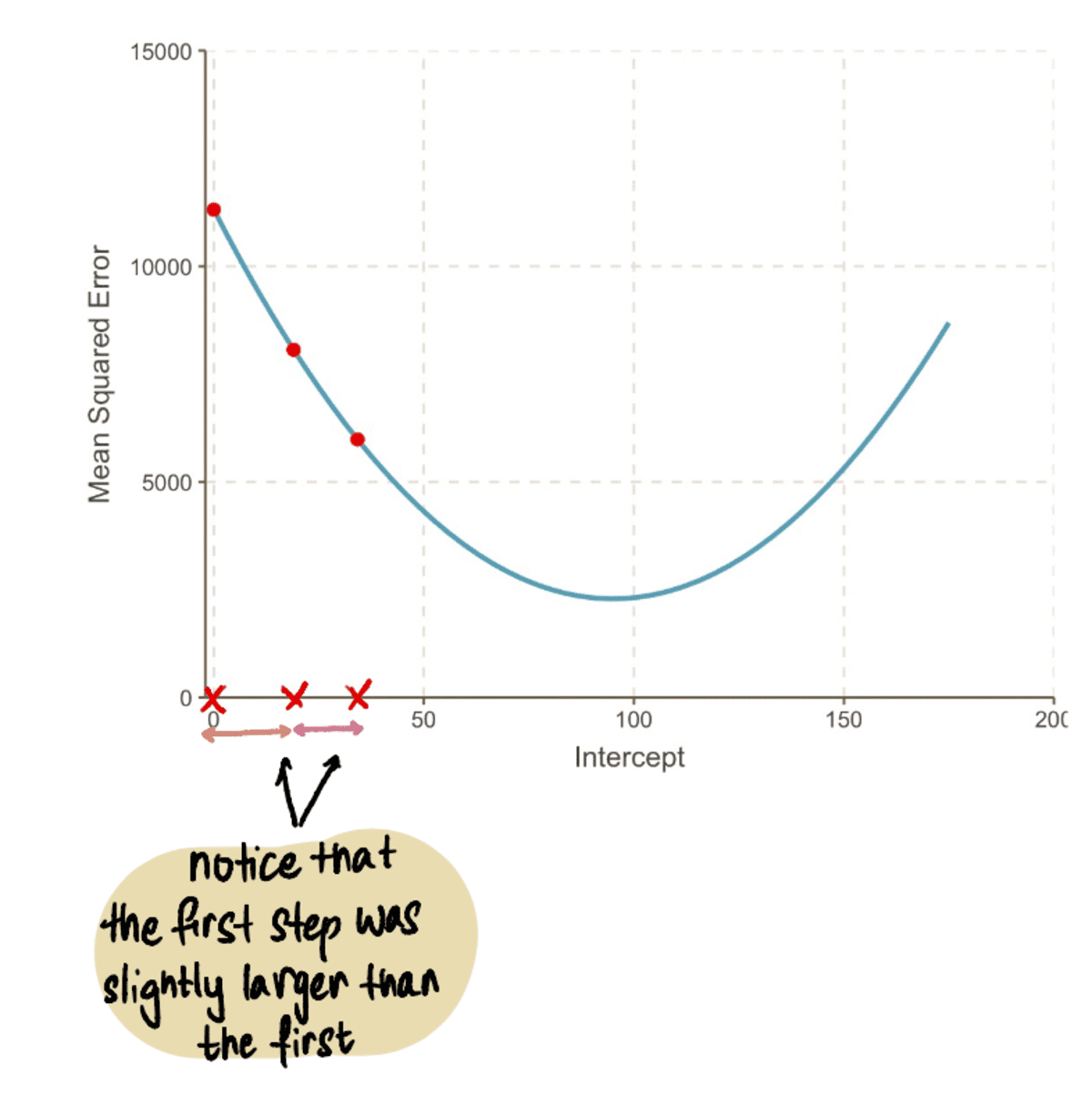
Kordame seda protsessi iteratiivselt, kuni jõuame optimaalse lahenduseni:

 

 

Kõvera miinimumpunkti poole liikudes täheldame, et Sammu suurus muutub järjest väiksemaks. Pärast 13 sammu hindab gradiendi laskumise algoritm pealtkuulamiseks väärtus on 95. Kui meil oleks kristallkuul, kinnitataks seda kui miinimumpunkti MSE kõver. Ja on selge, kuidas see meetod on tõhusam võrreldes toore jõu lähenemisviisiga, mida nägime artiklis Eelmine artikkel.

Nüüd, kui meil on oma optimaalne väärtus pealtkuulamiseks, on lineaarse regressiooni mudel:

 

 

Ja lineaarne regressioonijoon näeb välja selline:

 

kõige paremini sobiv joon lõikepunktiga = 95 ja kaldega = 0.069

 

Lõpetuseks, tulles tagasi meie sõbra Marki küsimuse juurde – millise väärtusega peaks ta oma 2400 jala² suuruse maja müüma?

 

 

Ühendage maja suurus 2400 jalga² ülaltoodud võrrandiga…

 

 

…ja voilaa. Võime oma asjatult murelikule sõbrale Markile öelda, et tema naabruses asuva kolme maja põhjal peaks ta oma maja müüma umbes 3 260,600 dollari eest.

Nüüd, kui oleme mõistetest hästi aru saanud, teeme kiire küsimuste ja vastuste sessiooni, et vastata kõikidele püsivatele küsimustele.

Miks gradiendi leidmine tegelikult töötab?

Selle illustreerimiseks mõelge stsenaariumile, kus me püüame jõuda kõvera C miinimumpunkti, mida tähistatakse kui x*. Ja praegu oleme punktis A kl x, mis asub vasakul x*:

 

 

Kui võtame kõvera tuletise punktis A suhtes x, esindatud kui dC(x)/dx, saame negatiivse väärtuse (see tähendab gradient on allapoole kaldu). Samuti täheldame, et jõudmiseks peame liikuma paremale x*. Seega peame suurendama x jõuda miinimumini x*.

 

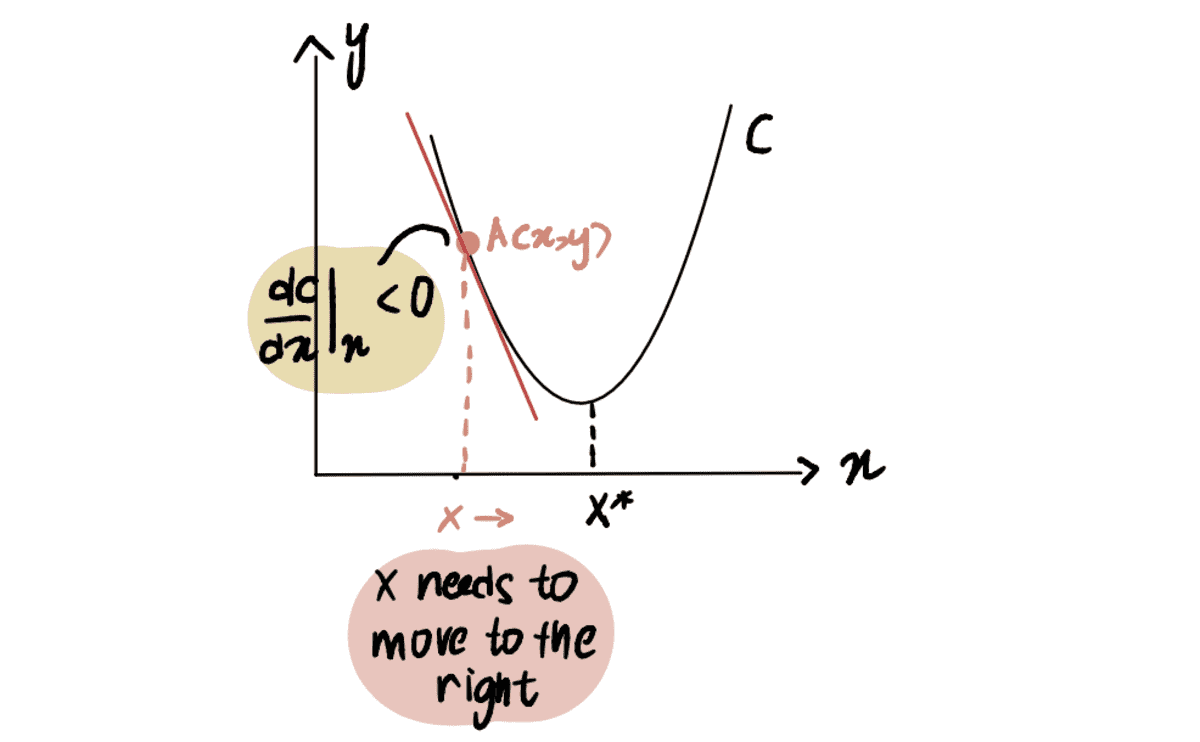
punane joon ehk gradient on allapoole kaldu => negatiivne gradient

 
 

Alates dC(x)/dx on negatiivne, x-??*dC(x)/dx saab olema suurem kui x, liikudes seega poole x*.

Samamoodi, kui oleme punktis A, mis asub miinimumpunktist x* paremal, siis saame a positiivne gradient (gradient on kaldu ülespoole), dC(x)/dx.

 

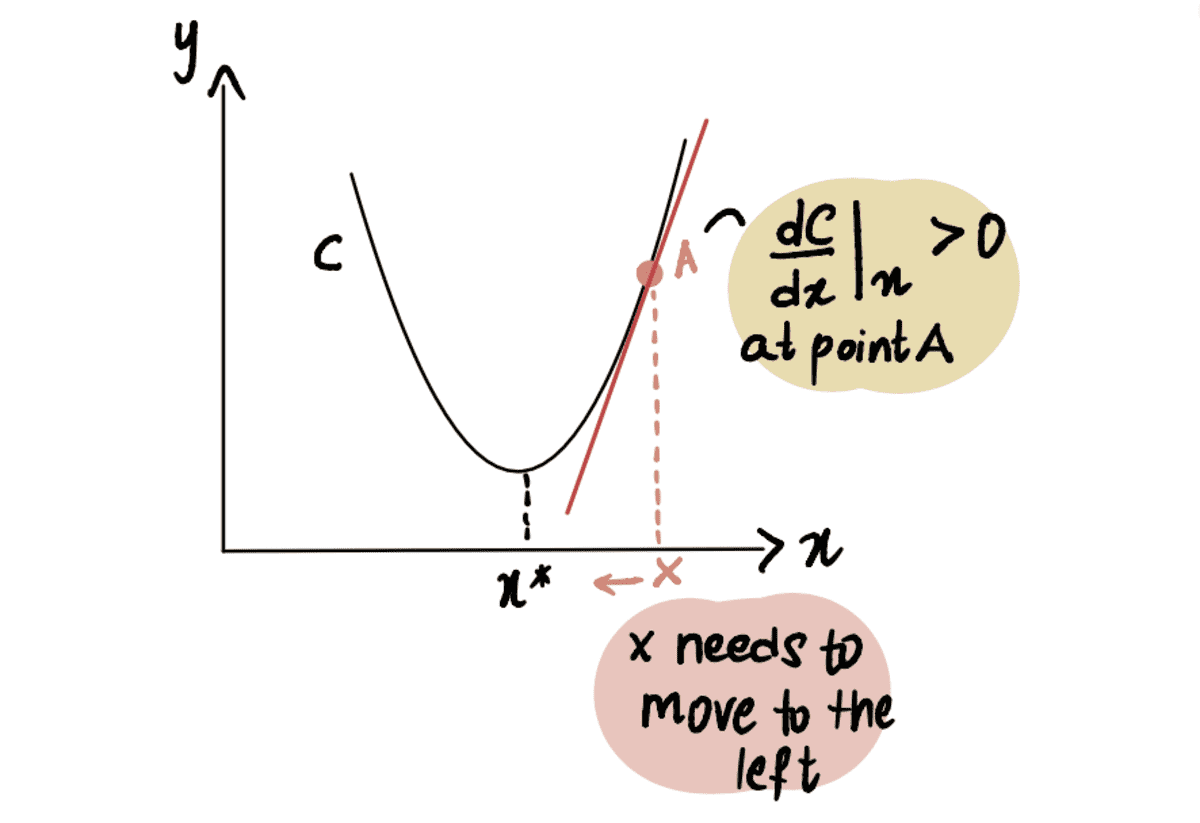
punane joon ehk gradient on ülespoole kaldu => positiivne gradient

 

So x-??*dC(x)/dx saab olema väiksem kui x, liikudes seega poole x*.

Kuidas gradient korralik teab, millal samme lõpetada?

Gradiendi laskumine peatub, kui Sammu suurus on väga lähedal 0-le. Nagu eelnevalt mainitud, on miinimumpunktis the gradient on 0 ja kui läheneme miinimumile, siis gradient läheneb 0-le. Seega, kui gradient punktis on 0-le lähedal või miinimumpunkti läheduses Sammu suurus on samuti 0-le lähedal, mis näitab, et algoritm on jõudnud optimaalse lahenduseni.

 

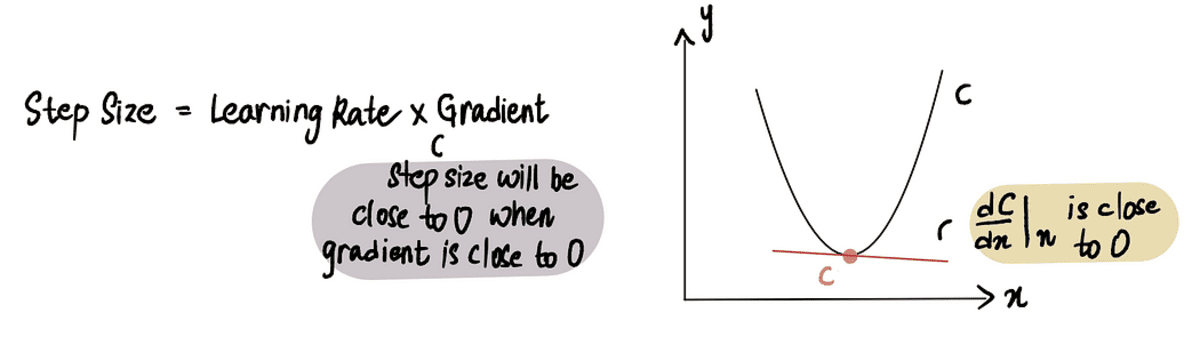
kui oleme miinimumpunkti lähedal, on gradient lähedane 0-le ja seejärel sammu suurus 0-le

Praktikas on sammu minimaalne suurus = 0.001 või väiksem

 

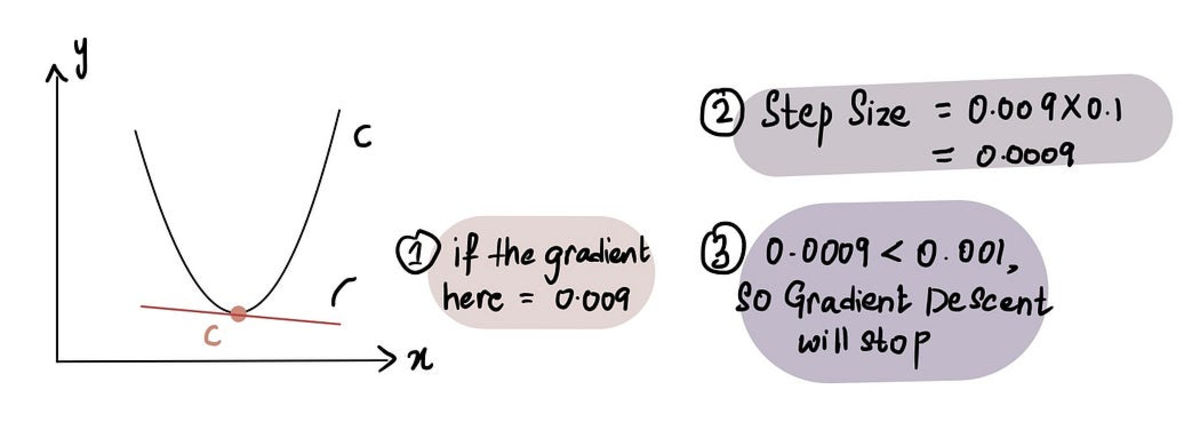
Nagu öeldud, hõlmab kallaku laskumine ka piirangut sammude arvule, mis tuleb teha enne loobumist Maksimaalne sammude arv.

Praktikas on sammude maksimaalne arv 1000 või rohkem

Nii et isegi kui Sammu suurus on suurem kui Minimaalne sammu suurus, kui neid on olnud rohkem kui Maksimaalne sammude arv, gradient laskumine peatub.

Mis siis, kui miinimumpunkti tuvastamine on keerulisem?

Seni oleme töötanud kõveraga, mille miinimumpunkti on lihtne tuvastada (sellised kõverad on nn. kumer). Aga mis siis, kui meil on kõver, mis pole nii ilus (tehniliselt aka mittekumer) ja näeb välja selline:

 

 

Siin näeme, et punkt B on globaalne miinimum (tegelik miinimum) ning punktid A ja C on kohalikud miinimumid (punktid, mida võib segamini ajada globaalne miinimum aga ei ole). Nii et kui funktsioonil on mitu kohalikud miinimumid ja globaalne miinimum, ei ole garanteeritud, et gradient laskumine leiab globaalne miinimum. Veelgi enam, milline kohalik miinimum see leiab, sõltub esialgse oletuse asukohast (nagu on näha Samm 1 gradient laskumine).

 

 

Võttes selle ülaltoodud mittekumera kõvera näitena, kui esialgne oletus on plokis A või plokis C, deklareerib gradiendi langus, et miinimumpunkt on vastavalt kohalikel miinimumidel A või C, kuigi tegelikkuses on see punktis B. Ainult siis, kui esialgne oletus on plokis B, leiab algoritm globaalse miinimumi B.

Nüüd on küsimus – kuidas teha hea esialgne oletus?

Lihtne vastus: Katse-eksitus meetod. Midagi sarnast.

Mitte nii lihtne vastus: Ülaltoodud graafiku põhjal, kui meie minimaalne oletus x oli 0, kuna see asub plokis A, viib see kohaliku miinimumini A. Seega, nagu näete, ei pruugi 0 enamikul juhtudel olla hea esialgne oletus. Levinud tava on rakendada juhuslikku funktsiooni, mis põhineb ühtlasel jaotusel x kõigi võimalike väärtuste vahemikus. Lisaks, kui see on teostatav, võib algoritmi käitamine erinevate esialgsete oletustega ja nende tulemuste võrdlemine anda ülevaate sellest, kas oletused erinevad üksteisest oluliselt. See aitab globaalset miinimumi tõhusamalt tuvastada.

Olgu, oleme peaaegu kohal. Viimane küsimus.

Mis siis, kui püüame leida rohkem kui ühte optimaalset väärtust?

Seni olime keskendunud ainult optimaalse lõikeväärtuse leidmisele, sest teadsime võluväel seda kalle lineaarse regressiooni väärtus on 0.069. Aga mis siis, kui sul pole kristallkuuli ja ei tea optimaalset kalle väärtus? Seejärel peame optimeerima nii kalde kui ka lõikeväärtusi, väljendatuna kujul x? ja x? võrra.

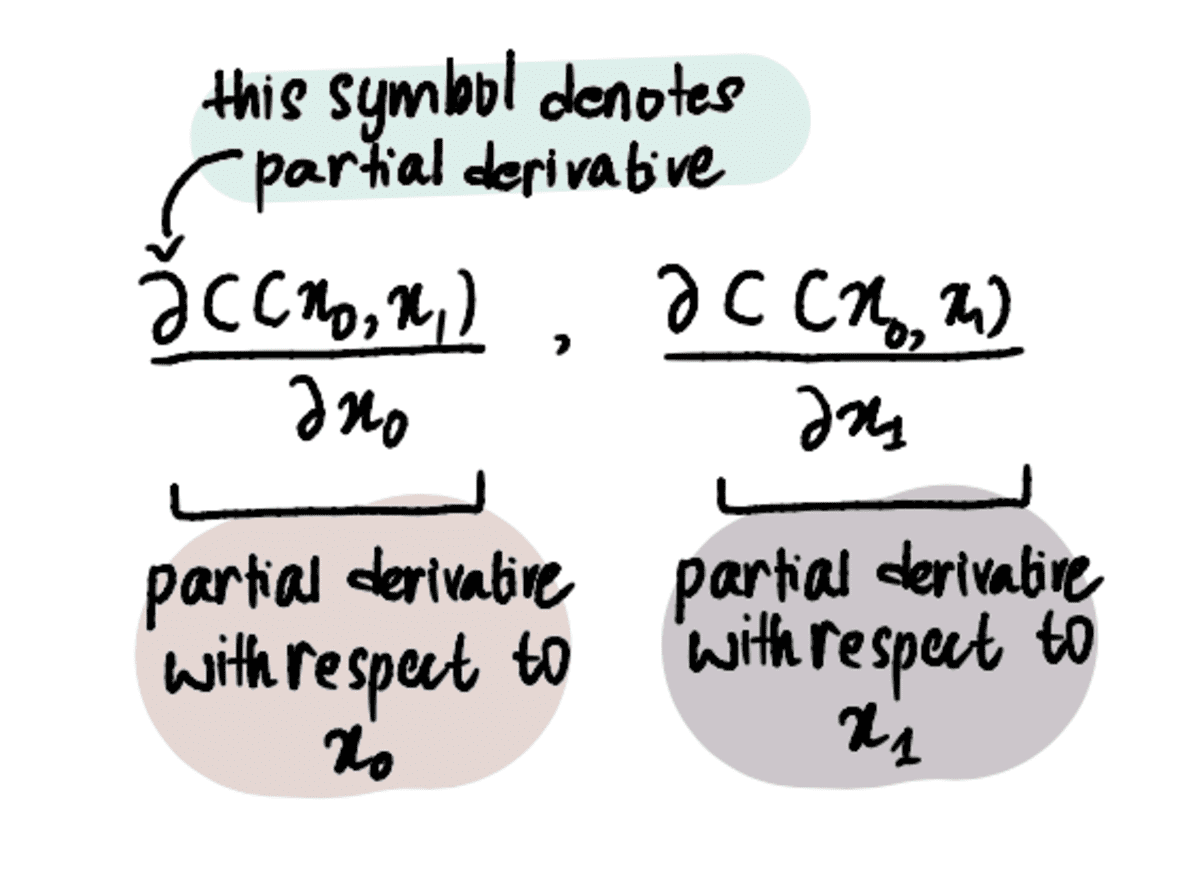
Selleks peame ainult tuletiste asemel kasutama osalisi tuletisi.

MÄRKUS. Osatuletised arvutatakse samamoodi nagu vanad reglar-tuletised, kuid neid tähistatakse erinevalt, kuna meil on rohkem kui üks muutuja, mille jaoks proovime optimeerida. Nende kohta lisateabe saamiseks lugege seda artikkel või vaadake seda video.

Protsess jääb siiski suhteliselt sarnaseks ühe väärtuse optimeerimise protsessiga. Kulufunktsioon (nt MSE). ja x?.

1. samm: tehke esialgsed oletused x₀ ja x₁ jaoks

2. samm: leidke nendes punktides osatuletised xXNUMX ja xXNUMX suhtes

 

 

3. samm: värskendage samaaegselt x₀ ja x₁ osatuletisi ja õppimiskiiruse põhjal

 

 

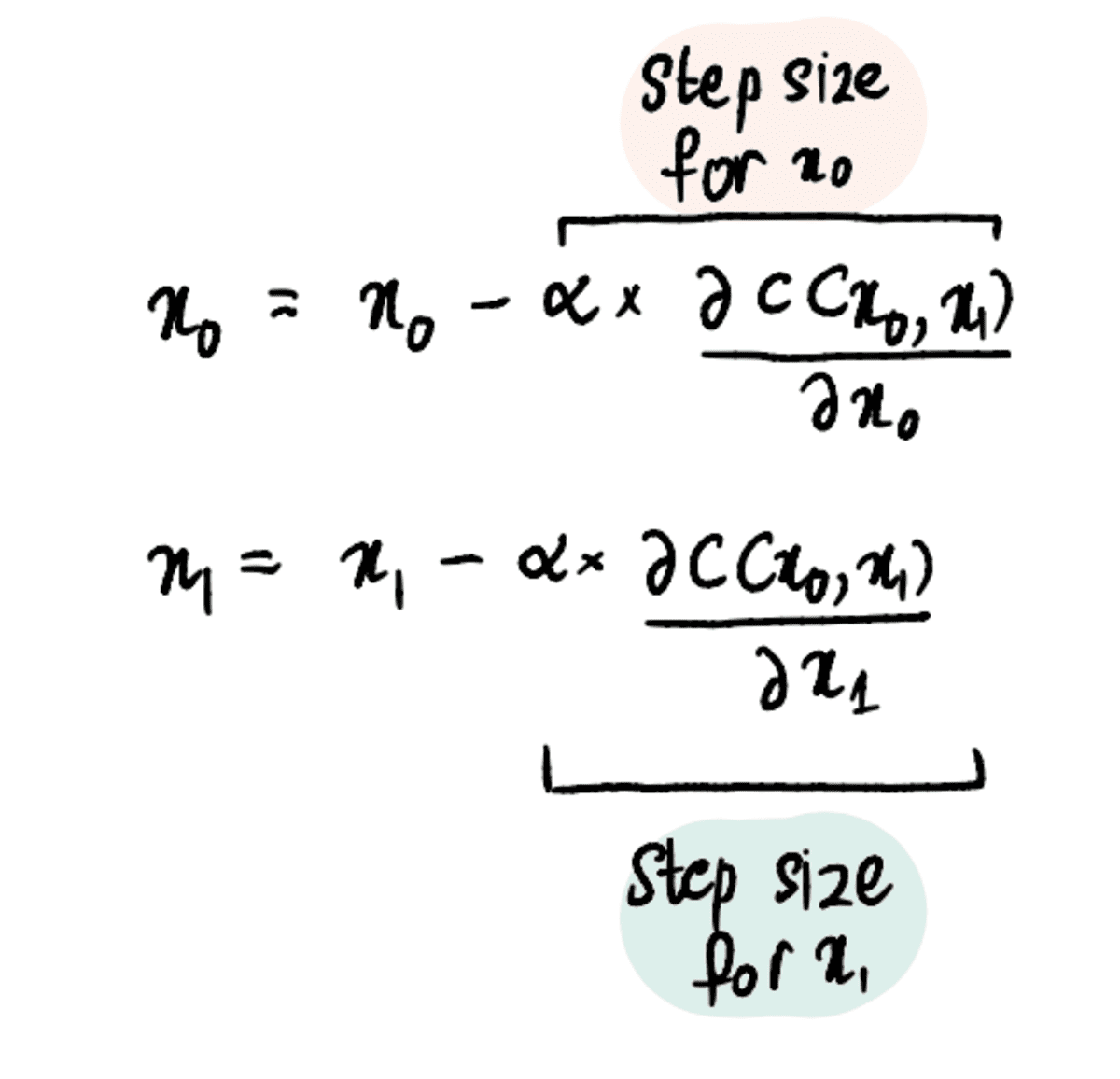
4. samm: korrake samme 2–3, kuni on saavutatud maksimaalne sammude arv või sammu suurus on väiksem kui sammude minimaalne suurus

Ja me saame need sammud optimeerimiseks ekstrapoleerida 3, 4 või isegi 100 väärtuseni.

Kokkuvõtteks võib öelda, et gradiendi laskumine on võimas optimeerimisalgoritm, mis aitab meil tõhusalt optimaalse väärtuseni jõuda. Gradiendi laskumisalgoritmi saab rakendada paljude muude optimeerimisprobleemide puhul, muutes selle andmeteadlaste arsenalis oluliseks tööriistaks. Nüüd suuremate ja paremate algoritmide juurde!

 
 
Shreya Rao illustreerige ja selgitage masinõppe algoritme võhiku terminites.

 
Originaal. Loaga uuesti postitatud.
 

• SEO-põhise sisu ja PR-levi. Võimenduge juba täna.
• Platoblockchain. Web3 metaversiooni intelligentsus. Täiustatud teadmised. Juurdepääs siia.
• Allikas: https://www.kdnuggets.com/2023/03/back-basics-part-dos-gradient-descent.html?utm_source=rss&utm_medium=rss&utm_campaign=back-to-basics-part-dos-gradient-descent