L’image de jauge de la dynamique quantique

L’image de jauge de la dynamique quantique

Horodatage: 21 mars 2024 6:43
Nœud source: 2521965

Kevin Slagle

Département de génie électrique et informatique, Rice University, Houston, Texas 77005 États-Unis
Département de physique, California Institute of Technology, Pasadena, Californie 91125, États-Unis
Institute for Quantum Information and Matter et Walter Burke Institute for Theoretical Physics, California Institute of Technology, Pasadena, Californie 91125, États-Unis

Vous trouvez cet article intéressant ou souhaitez en discuter? Scite ou laisse un commentaire sur SciRate.

Abstract

Bien que les hamiltoniens locaux présentent une dynamique temporelle locale, cette localité n'est pas explicite dans l'image de Schrödinger dans le sens où les amplitudes de la fonction d'onde n'obéissent pas à une équation locale du mouvement. Nous montrons que la localité géométrique peut être obtenue explicitement dans les équations du mouvement en « évaluant » l’invariance unitaire globale de la mécanique quantique en une invariance de jauge locale. Autrement dit, les valeurs d'espérance $langle psi|A|psi rangle$ sont invariantes sous une transformation unitaire globale agissant sur la fonction d'onde $|psirangle en U |psirangle$ et les opérateurs $A vers UAU^dagger$, et nous montrons que c'est possible pour évaluer cette invariance globale en une invariance de jauge locale. Pour ce faire, nous remplaçons la fonction d'onde par une collection de fonctions d'onde locales $|psi_Jrangle$, une pour chaque morceau d'espace $J$. L'ensemble des patchs spatiaux est choisi pour couvrir l'espace ; par exemple, nous pourrions choisir que les correctifs soient des qubits uniques ou des sites voisins les plus proches sur un réseau. Les fonctions d'onde locales associées aux paires voisines de patchs spatiaux $I$ et $J$ sont liées les unes aux autres par des transformations unitaires dynamiques $U_{IJ}$. Les fonctions d'onde locales sont locales dans le sens où leur dynamique est locale. Autrement dit, les équations de mouvement pour les fonctions d'onde locales $|psi_Jrangle$ et les connexions $U_{IJ}$ sont explicitement locales dans l'espace et ne dépendent que de termes hamiltoniens proches. (Les fonctions d'onde locales sont des fonctions d'onde à plusieurs corps et ont la même dimension spatiale de Hilbert que la fonction d'onde habituelle.) Nous appelons cette image de la dynamique quantique l'image de jauge car elle présente une invariance de jauge locale. La dynamique locale d'une seule parcelle spatiale est liée à l'image d'interaction, où l'hamiltonien d'interaction est constitué uniquement de termes hamiltoniens proches. Nous pouvons également généraliser la localité explicite pour inclure la localité dans les densités de charge et d'énergie locales.

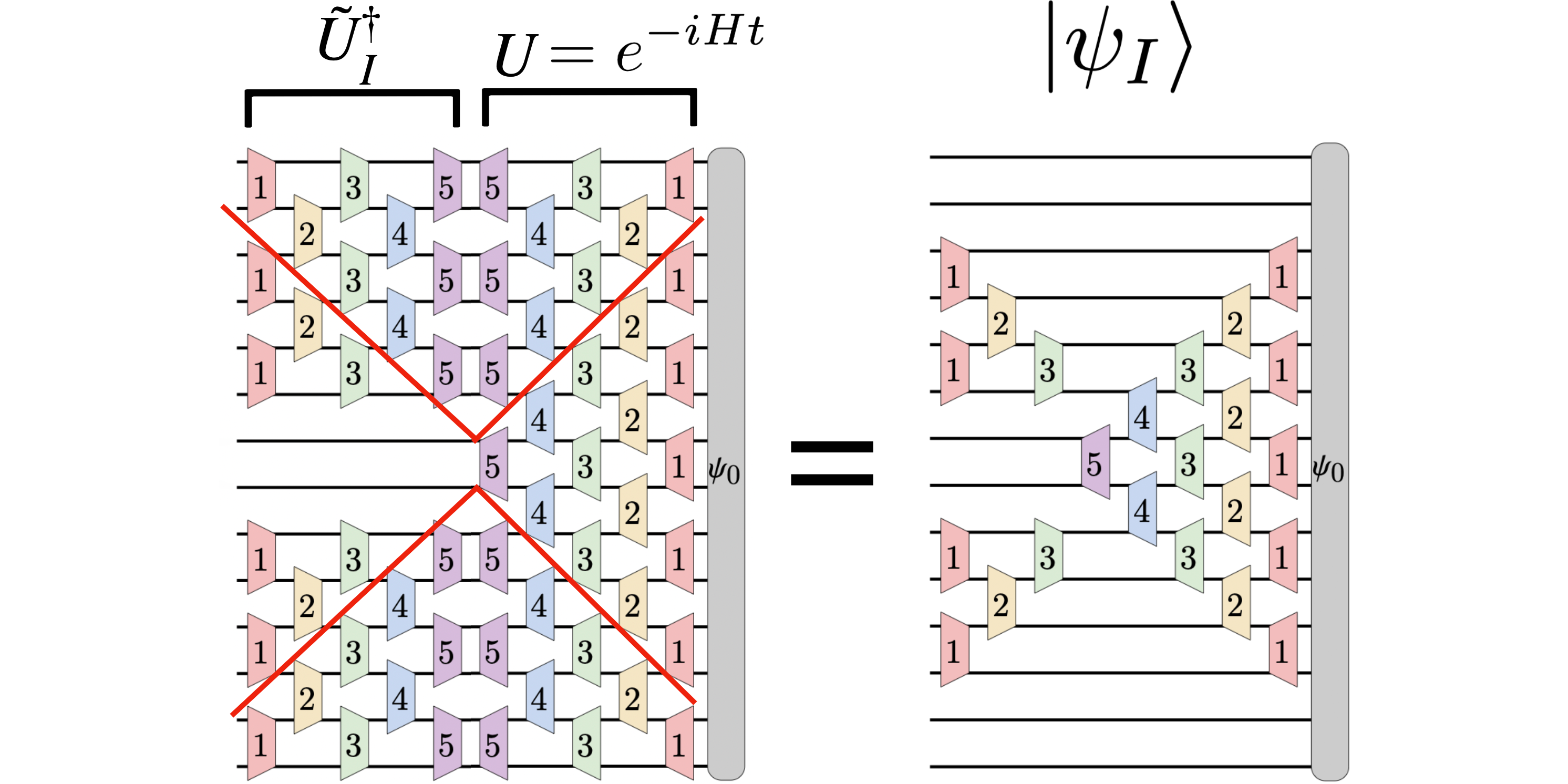
Image présentée : Dans l'image de Schrödinger, une fonction d'onde initiale $|psi_0rangle$ évolue vers $U(t) |psi_0rangle$ après un temps $t$, où $U(t) = e^{-iHt}$ est l'évolution temporelle unitaire opérateur. L'image de la jauge considère à la place les fonctions d'onde locales $|psi_I(t)rangle$ qui sont associées à un sous-ensemble (ou patch) $I$ dans l'espace. La fonction d'onde locale évoluée dans le temps $|psi_I(t)rangle = tilde{U}_I^dagger(t) |psi(t)rangle$ est obtenue à partir de la fonction d'onde de Schrödinger $|psi(t)rangle = U(t) |psi_0rangle $ via l'opérateur unitaire $tilde{U}_I^dagger(t)$, qui inverse l'évolution temporelle en dehors de la région $I$. En conséquence, la dynamique de la fonction d'onde locale $partial_I |psi_I(t)rangle$ ne dépend que des termes hamiltoniens proches qui chevauchent la région $I$. La figure représente ces opérateurs unitaires comme des circuits quantiques et démontre qu'une grande partie de l'évolution temporelle à partir de $U(t)$ s'annule avec $tilde{U}_I^dagger(t)$, ne laissant qu'un opérateur d'évolution temporelle en forme de sablier. agissant sur la fonction d'onde initiale (à droite de la figure). Cet opérateur en forme de sablier est analogue à la croissance de l'opérateur en forme de cône lumineux dans l'image de Heisenberg.

Résumé populaire

Les deux images les plus célèbres de la dynamique quantique sont les images de Schrödinger et de Heisenberg. Dans l'image de Schrödinger, la fonction d'onde évolue dans le temps, tandis que dans l'image de Heisenberg, la fonction d'onde est constante mais les opérateurs évoluent dans le temps. Dans ce travail, nous introduisons une nouvelle image de la dynamique quantique, l’image de jauge, qui établit des liens profonds avec la localité de l’information et la théorie de jauge.

Concernant la localité : un avantage appréciable de l'image de Heisenberg est que la localité est explicite dans les équations du mouvement. Autrement dit, l’évolution temporelle d’un opérateur local dépend uniquement de l’état des opérateurs locaux proches. En revanche, la localité n'est pas explicite de cette manière dans l'image de Schrödinger, pour laquelle il existe une seule fonction d'onde dont la dynamique temporelle dépend d'opérateurs partout dans l'espace. Notre nouvelle image de jauge modifie l'image de Schrödinger de telle sorte que nous pouvons calculer une « fonction d'onde locale » qui transporte les mêmes informations que la fonction d'onde de Schrödinger. Attendez-vous à ce que la dynamique temporelle des fonctions d'onde locales dans l'image de jauge ne dépende que des termes hamiltoniens proches, ce qui rend la localité explicite dans le équations du mouvement. Afin d'obtenir cette localité explicite, l'image de jauge ajoute des champs de jauge aux équations du mouvement.

La théorie de jauge établit un lien profond entre un hamiltonien (ou lagrangien) avec une symétrie globale et un autre hamiltonien où la symétrie globale est remplacée par une symétrie de jauge locale via l'addition de champs de jauge dynamiques. Fait intéressant, l'équation de Schrödinger $ihbar partial_t |psirangle = H |psirangle$ admet une invariance unitaire globale donnée par la transformation $|psirangle en U |psirangle$ et $H en UHU^dagger$. Nos travaux montrent qu'il est également possible d'appliquer la théorie de jauge à cette invariance globale dans l'équation de Schrödinger pour obtenir une nouvelle équation du mouvement, ie l'image de jauge, avec des champs de jauge dynamiques et une invariance de jauge locale.

► Données BibTeX

► Références

David Deutsch et Patrick Hayden. "Flux d'informations dans les systèmes quantiques intriqués". Actes de la Royal Society of London, série A 456, 1759 (2000). arXiv:quant-ph/​9906007.
https: / / doi.org/ 10.1098 / rspa.2000.0585
arXiv: quant-ph / 9906007

Michael A. Levin et Xiao-Gang Wen. "Condensation String-net: Un mécanisme physique pour les phases topologiques". Phys. Rév.B 71, 045110 (2005). arXiv:cond-mat/​0404617.
https: / / doi.org/ 10.1103 / PhysRevB.71.045110
arXiv: cond-mat / 0404617

T. Senthil, Ashvin Vishwanath, Leon Balents, Subir Sachdev et Matthew PA Fisher. « Points critiques quantiques déconfinés ». Sciences 303, 1490-1494 (2004). arXiv:cond-mat/​0311326.
https: / / doi.org/ 10.1126 / science.1091806
arXiv: cond-mat / 0311326

Beni Yoshida. "Ordre topologique exotique dans les liquides de spin fractal". Phys. Rév.B 88, 125122 (2013). arXiv : 1302.6248.
https: / / doi.org/ 10.1103 / PhysRevB.88.125122
arXiv: 1302.6248

Kévin Hartnett. "La multiplication matricielle se rapproche de l'objectif mythique". Revue Quanta (2021). URL : https://​/​www.quantamagazine.org/​mathematicians-inch-closer-to-matrix-multiplication-goal-20210323/​.
https://​/​www.quantamagazine.org/​mathematicians-inch-closer-to-matrix-multiplication-goal-20210323/​

Volker Strassen. "L'élimination gaussienne n'est pas optimale". Numerische Mathematik 13, 354-356 (1969).
https: / / doi.org/ 10.1007 / BF02165411

Kevin Slagle. "Réseaux de jauge quantique : un nouveau type de réseau tenseur". Quantique 7, 1113 (2023). arXiv :2210.12151.
https:/​/​doi.org/​10.22331/​q-2023-09-14-1113
arXiv: 2210.12151

Roman Orús. "Une introduction pratique aux réseaux de tenseurs : états de produits matriciels et états de paires intriquées projetés". Annales de physique 349, 117-158 (2014). arXiv : 1306.2164.
https: / / doi.org/ 10.1016 / j.aop.2014.06.013
arXiv: 1306.2164

Michael P. Zaletel et Frank Pollmann. «États du réseau tensoriel isométrique en deux dimensions». Phys. Le révérend Lett. 124, 037201 (2020). arXiv : 1902.05100.
https: / / doi.org/ 10.1103 / PhysRevLett.124.037201
arXiv: 1902.05100

Steven Weinberg. « Tester la mécanique quantique ». Annales de physique 194, 336-386 (1989).
https:/​/​doi.org/​10.1016/​0003-4916(89)90276-5

N. Gisin. "La mécanique quantique non linéaire et les communications supraluminales de Weinberg". Lettres de physique A 143, 1–2 (1990).
https:/​/​doi.org/​10.1016/​0375-9601(90)90786-N

Joseph Polchinski. « La mécanique quantique non linéaire de Weinberg et le paradoxe d'Einstein-Podolsky-Rosen ». Phys. Le révérend Lett. 66, 397-400 (1991).
https: / / doi.org/ 10.1103 / PhysRevLett.66.397

Kevin Slagle. « Test de la mécanique quantique à l'aide d'ordinateurs quantiques bruyants » (2021). arXiv :2108.02201.
arXiv: 2108.02201

Brian Swingle. "Déchiffrer la physique des corrélateurs hors ordre temporel". Physique de la nature 14, 988-990 (2018).
https:/​/​doi.org/​10.1038/​s41567-018-0295-5

Ignacio García-Mata, Rodolfo A. Jalabert et Diego A. Wisniacki. « Corrélateurs d'ordre hors du temps et chaos quantique » (2022). arXiv :2209.07965.
arXiv: 2209.07965

Rahul Nandkishore et David A. Huse. « Localisation à plusieurs corps et thermalisation en mécanique statistique quantique ». Revue annuelle de la physique de la matière condensée 6, 15-38 (2015). arXiv : 1404.0686.
https: / / doi.org/ 10.1146 / annurev-conmatphys-031214-014726
arXiv: 1404.0686

Dmitry A. Abanin, Ehud Altman, Immanuel Bloch et Maksym Serbyn. « Colloque : Localisation à N corps, thermalisation et intrication ». Examens de Physique moderne 91, 021001 (2019). arXiv : 1804.11065.
https: / / doi.org/ 10.1103 / RevModPhys.91.021001
arXiv: 1804.11065

Bruno Nachtergaele et Robert Sims. « Beaucoup de bruit pour quelque chose : pourquoi les limites de Lieb-Robinson sont utiles » (2011). arXiv : 1102.0835.
arXiv: 1102.0835

Daniel A. Roberts et Brian Swingle. "La liaison Lieb-Robinson et l'effet papillon dans les théories quantiques des champs". Phys. Le révérend Lett. 117, 091602 (2016). arXiv : 1603.09298.
https: / / doi.org/ 10.1103 / PhysRevLett.117.091602
arXiv: 1603.09298

Zhiyuan Wang et Kaden RA Hazzard. « Rerrer la liaison Lieb-Robinson dans les systèmes à interaction locale ». PRX Quantique 1, 010303 (2020). arXiv : 1908.03997.
https: / / doi.org/ 10.1103 / PRXQuantum.1.010303
arXiv: 1908.03997

Cité par

[1] Sayak Guha Roy et Kevin Slagle, « Interpolation entre la jauge et les images de Schrödinger de la dynamique quantique », SciPost Physique Core 6 4, 081 (2023).

[2] Kevin Slagle, « Réseaux de jauge quantique : un nouveau type de réseau tensoriel », Quantique 7, 1113 (2023).

Les citations ci-dessus proviennent de SAO / NASA ADS (dernière mise à jour réussie 2024-03-21 22:55:07). La liste peut être incomplète car tous les éditeurs ne fournissent pas de données de citation appropriées et complètes.

On Le service cité par Crossref aucune donnée sur la citation des œuvres n'a été trouvée (dernière tentative 2024-03-21 22:55:05).

Cet article est publié dans Quantum sous le Creative Commons Attribution 4.0 International (CC BY 4.0) Licence. Le droit d'auteur reste la propriété des détenteurs d'origine tels que les auteurs ou leurs institutions.

Horodatage:

Plus de Journal quantique