क्वांटम फील्ड थ्योरी खुली गणितीय पहेली

पिछले महीने, करेन वोग्टमैन और माइकल बोरिंस्की एक प्रमाण पोस्ट किया कि अब तक दुर्गम गणितीय दुनिया के भीतर गणितीय संरचना का एक ट्रक भरा हुआ है जिसे ग्राफ़ का मॉड्यूली स्पेस कहा जाता है, जिसे वोग्टमैन और एक सहयोगी पहले वर्णित मध्य 1980 में

“यह एक अत्यंत कठिन समस्या है। यह आश्चर्यजनक है कि वे ऐसा करने में सक्षम थे, ”जॉर्जिया इंस्टीट्यूट ऑफ टेक्नोलॉजी के गणितज्ञ डैन मार्गालिट ने कहा।

वोग्टमैन और बोरिंस्की ने उन सवालों से शुरुआत की जो वारविक विश्वविद्यालय के गणितज्ञ वोग्टमैन दशकों से खुद से पूछ रहे थे। इसके बाद इस जोड़ी ने क्वांटम क्षेत्र सिद्धांत की तकनीकों का उपयोग करके अपने परिणाम तक पहुंचने के लिए भौतिकी की भाषा में इस मुद्दे की फिर से कल्पना की।

प्रमाण दर्शाता है कि मॉड्यूलि स्पेस में कुछ संरचनाएँ मौजूद हैं, लेकिन यह स्पष्ट रूप से प्रकट नहीं करता है कि वे संरचनाएँ क्या हैं। इस तरह, उनका नया परिणाम कैमरे की तुलना में मेटल डिटेक्टर की तरह है - यह उन्हें सचेत करता है कि कुछ दिलचस्प छिपा हुआ है, भले ही वे इसका पूरी तरह से वर्णन नहीं कर सकते।

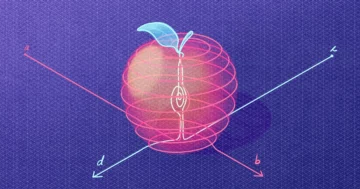
आप ग्राफ़ के मॉड्यूलि स्पेस को अतिरिक्त सजावट के साथ गणितीय आकृतियों के रूप में सोच सकते हैं। यदि आप आकृति के किसी भी बिंदु पर खड़े हैं, तो आप अपने ऊपर तैरता हुआ एक ग्राफ़ देखेंगे - किनारों से जुड़े बिंदुओं या शीर्षों का एक संग्रह। मॉड्यूलि स्पेस पर विभिन्न स्थानों पर, ग्राफ़ बदलते हैं, उनके किनारे सिकुड़ते या बढ़ते हैं, और कभी-कभी पूरी तरह से गायब हो जाते हैं। इन विशेषताओं के कारण, स्विस फेडरल इंस्टीट्यूट ऑफ टेक्नोलॉजी ज्यूरिख के गणितीय भौतिक विज्ञानी बोरिंस्की, मॉड्यूलि स्पेस को "ग्राफ़ का एक बड़ा समुद्र" के रूप में वर्णित करते हैं।

किसी ग्राफ़ की "रैंक" उसमें मौजूद लूपों की संख्या है; ग्राफ़ के प्रत्येक रैंक के लिए, एक मॉड्यूलि स्पेस मौजूद होता है। इस स्थान का आकार तेज़ी से बढ़ता है - यदि आप ग्राफ़ के किनारों की लंबाई तय करते हैं, तो रैंक 2 के तीन ग्राफ़, रैंक 15 के 3, रैंक 111 के 4 और रैंक 2,314,204,852 के 10 होते हैं। मॉड्यूलि स्पेस पर, ये लंबाई हो सकती हैं भिन्न-भिन्न, और भी अधिक जटिलता का परिचय देते हुए।

किसी दिए गए रैंक के ग्राफ़ के लिए मॉड्यूलि स्पेस का आकार ग्राफ़ के बीच संबंधों द्वारा निर्धारित किया जाता है। जैसे ही आप अंतरिक्ष में घूमते हैं, आस-पास के ग्राफ़ समान होने चाहिए, और एक दूसरे में आसानी से रूपांतरित होने चाहिए। लेकिन ये रिश्ते जटिल हैं, जिससे मॉड्यूलि स्पेस में गणितीय रूप से अस्थिर विशेषताएं रह जाती हैं, जैसे कि ऐसे क्षेत्र जहां मॉड्यूलि स्पेस की तीन दीवारें एक दूसरे से होकर गुजरती हैं।

गणितज्ञ कोहोमोलॉजी कक्षाओं नामक वस्तुओं का उपयोग करके किसी स्थान या आकृति की संरचना का अध्ययन कर सकते हैं, जो यह बताने में मदद कर सकता है कि किसी स्थान को एक साथ कैसे रखा जाता है। उदाहरण के लिए, गणितज्ञों की पसंदीदा आकृतियों में से एक डोनट पर विचार करें। डोनट पर, कोहोमोलॉजी कक्षाएं केवल लूप हैं।

डोनट की सतह पर कई अलग-अलग प्रकार के लूप बनाए जा सकते हैं: लूप 1 डोनट के केंद्रीय छेद को घेरता है; छेद के माध्यम से 2 धागे लूप करें; तीसरा "तुच्छ" लूप डोनट की तरफ बैठता है।

हालाँकि, सभी कोहोमोलॉजी कक्षाएं समान नहीं बनाई गई हैं। डोनट के बाहर बैठा एक लूप - तीसरे लूप की तरह - दूसरे लूप को काटने से बचने के लिए हमेशा इधर-उधर खिसक सकता है या सिकुड़ सकता है। यह इसे एक "तुच्छ" कोहॉमोलॉजी वर्ग बनाता है।

लेकिन लूप 1 और 2 डोनट की संरचना के बारे में बहुत कुछ कहते हैं - वे केवल छेद के कारण मौजूद हैं। अंतर को गणितीय रूप से समझने के लिए, आप प्रतिच्छेदन का उपयोग कर सकते हैं, मार्गालिट ने समझाया। लूप 1 और 2 डोनट की सतह पर घूम सकते हैं, लेकिन जब तक आप उन्हें सतह से पूरी तरह से अलग होने के लिए मजबूर नहीं करते, वे हमेशा एक-दूसरे को काटते रहेंगे। क्योंकि ये दो लूप साझेदारों के साथ आते हैं जिन्हें वे पार करने में मदद नहीं कर सकते, वे "गैर-तुच्छ" कोहोलॉजी कक्षाएं हैं।

डोनट के विपरीत, गणितज्ञ केवल एक चित्र बनाकर ग्राफ़ के मॉड्यूलि स्थानों पर कोहोलॉजी कक्षाएं नहीं ढूंढ सकते हैं। कोपेनहेगन विश्वविद्यालय के गणितज्ञ नथाली वाहल ने कहा, इतनी बड़ी संख्या में ग्राफ़ के साथ, मॉड्यूलि स्पेस को संभालना मुश्किल है। "बहुत जल्दी, कंप्यूटर अब मदद नहीं कर सकता," उसने कहा। वास्तव में, केवल एक विषम-आयामी गैर-तुच्छ सह-समरूपता वर्ग रहा है स्पष्ट रूप से गणना की गई (11 आयामों में), मुट्ठी भर सम आयामों के साथ।

वोग्टमैन और बोरिंस्की ने जो साबित किया वह यह है कि बड़ी संख्या में कोहोलॉजी कक्षाएं हैं जो किसी दिए गए रैंक के ग्राफ़ के मॉड्यूलि स्पेस के भीतर स्थित हैं - भले ही हम उन्हें ढूंढ नहीं सकते। "हम जानते हैं कि बहुत सारे हैं, और हम एक को जानते हैं," वाहल ने स्थिति को "हास्यास्पद" बताते हुए कहा।

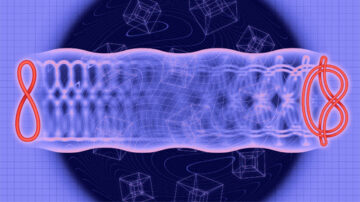
कोहोमोलॉजी कक्षाओं के साथ सीधे काम करने के बजाय, बोरिंस्की और वोग्टमैन ने यूलर विशेषता नामक एक संख्या का अध्ययन किया। यह संख्या मॉड्यूलि स्पेस का एक प्रकार का माप प्रदान करती है। आप मॉड्यूलि स्पेस को उसकी यूलर विशेषता को बदले बिना कुछ खास तरीकों से संशोधित कर सकते हैं, जिससे यूलर विशेषता स्वयं कोहोमोलॉजी कक्षाओं की तुलना में अधिक सुलभ हो जाती है। और बोरिंस्की और वोग्टमैन ने यही किया। ग्राफ़ के मॉड्यूलि स्पेस के साथ सीधे काम करने के बजाय, उन्होंने "रीढ़" का अध्ययन किया - अनिवार्य रूप से समग्र स्थान का एक कंकाल। रीढ़ की हड्डी में मॉड्यूलि स्पेस के समान ही यूलर विशेषता होती है और इसके साथ काम करना आसान होता है। रीढ़ की हड्डी पर यूलर विशेषता की गणना ग्राफ़ के जोड़े के एक बड़े संग्रह की गणना करने के लिए नीचे आई।

बोरिंस्की की अंतर्दृष्टि फेनमैन आरेखों की गिनती के लिए तकनीकों का उपयोग करना था, जो ग्राफ़ हैं जो क्वांटम कणों के संपर्क के तरीकों का प्रतिनिधित्व करते हैं। जब भौतिक विज्ञानी इस संभावना की गणना करना चाहते हैं कि एक इलेक्ट्रॉन और एक पॉज़िट्रॉन के बीच टकराव से दो फोटॉन उत्पन्न होंगे, तो उन्हें इसकी आवश्यकता होती है सभी संभावित अंतःक्रियाओं का योग जो उस परिणाम की ओर ले जाता है। इसका मतलब है कि कई फेनमैन आरेखों का औसत निकालना, चतुर गणना रणनीतियों को प्रेरित करना।

"मुझे एहसास हुआ कि कोई इस तरह की समस्या को एक खिलौना क्वांटम क्षेत्र सिद्धांत ब्रह्मांड के रूप में तैयार कर सकता है," बोरिंस्की ने समझाया।

बोरिंस्की ने ब्रह्मांड के एक सरल संस्करण में भौतिक प्रणालियों का प्रतिनिधित्व करने वाले ग्राफ़ की कल्पना की, जिसमें अन्य मान्यताओं के अलावा, केवल एक प्रकार का कण होता है। क्वांटम क्षेत्र सिद्धांत ढांचे को सही गणना प्राप्त करने के लिए बोरिंस्की और वोग्टमैन को कुछ समायोजन की आवश्यकता थी। उदाहरण के लिए, क्वांटम क्षेत्र सिद्धांत में, दो ग्राफ़ जो एक दूसरे की दर्पण छवियां हैं, अप्रभेद्य हैं, बोरिंस्की ने कहा। फेनमैन आरेखों को जोड़ने के सूत्रों में ऐसे कारक शामिल हैं जो सुनिश्चित करते हैं कि इन ग्राफ़ों की अधिक गणना नहीं की जाए। लेकिन जब यूलर विशेषता की गणना करने की बात आती है, तो उन ग्राफ़ को अलग माना जाता है। बोरिंस्की ने कहा, "हमें ग्राफ़ की समरूपता के साथ थोड़ा खेल खेलना होगा।"

भौतिक विज्ञानी की कुछ प्रोग्रामिंग सहायता से जोस वर्मासेरेन, बोरिंस्की और वोग्टमैन ने अंततः इस कठिनाई पर काबू पा लिया। अपने जनवरी पेपर में, उन्होंने साबित किया कि रैंक के ग्राफ़ के मॉड्यूलि स्पेस की यूलर विशेषता n के रूप में बड़े पैमाने पर नकारात्मक हो जाता है n बड़ा हो जाता है. इसका तात्पर्य यह है कि प्रत्येक मॉड्यूली स्थान के भीतर कई, कई गैर-तुच्छ कोहोलॉजी कक्षाएं उजागर की जानी हैं।

हालाँकि बोरिन्स्की और वोग्टमैन के पेपर में इन कोहोलॉजी कक्षाओं के बारे में कोई और संकेत नहीं है, यह उन शोधकर्ताओं के लिए एक उत्साहजनक परिणाम है जो उन्हें ढूंढना चाहते हैं - और शायद यह शिकार के रोमांच को बढ़ाता है। कोहोमोलॉजी कक्षाओं के मार्गालिट ने कहा: “जिन्हें हम जानते हैं वे सिर्फ ये रत्न हैं। और जब भी हमें कोई मिलता है, तो वह बहुत खूबसूरत चीज़ होती है।''