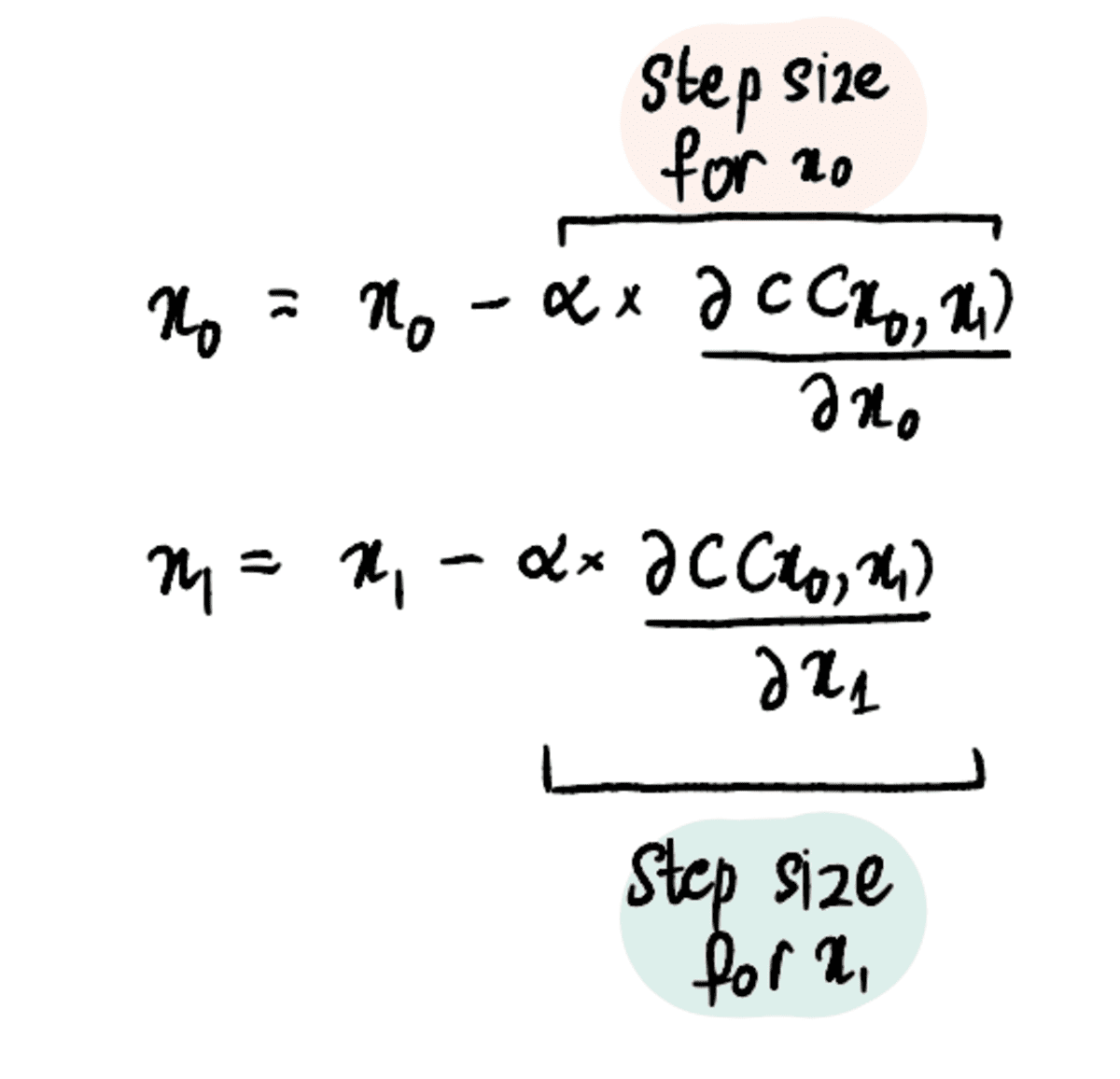Vissza az alapokhoz, Dos rész: Gradiens süllyedés

Üdvözöljük lapunk második részében Vissza az alapokhoz sorozat. Ban,-ben első rész, kitértünk arra, hogyan használhatjuk a lineáris regressziót és a költségfüggvényt, hogy megtaláljuk a legmegfelelőbb sort a lakásárak adataihoz. Azonban azt is láttuk, hogy a tesztelés többször is történt feltartóztat az értékek fárasztóak és nem hatékonyak lehetnek. Ebben a második részben mélyebbre ásunk a Gradient Descentben, egy erőteljes technikában, amely segíthet megtalálni a tökéleteset. feltartóztat és optimalizáljuk a modellünket. Megvizsgáljuk a mögöttes matematikát, és meglátjuk, hogyan alkalmazható a lineáris regressziós problémánkra.

A gradiens süllyedés egy hatékony optimalizálási algoritmus, amely célja, hogy gyorsan és hatékonyan megtalálja a görbe minimumpontját. Ennek a folyamatnak a legjobb módja az, ha elképzeled, hogy egy domb tetején állsz, és egy arannyal teli kincsesláda vár rád a völgyben.

 

 

A völgy pontos elhelyezkedése azonban ismeretlen, mert kint rendkívül sötét van, és nem látni semmit. Sőt, előbb akarod elérni a völgyet, mint bárki más (mert az összes kincset magadnak szeretnéd, duh). A gradiens ereszkedés segít eligazodni a terepen és elérni ezt optimálisan pont hatékonyan és gyorsan. Minden ponton megmondja, hány lépést kell megtennie, és milyen irányban kell megtennie azokat.

Hasonlóképpen a gradiens süllyedés is alkalmazható a lineáris regressziós feladatunkra az algoritmus által meghatározott lépések segítségével. A minimum megtalálásának folyamatának megjelenítéséhez ábrázoljuk a MSE ív. Már tudjuk, hogy a görbe egyenlete:

 

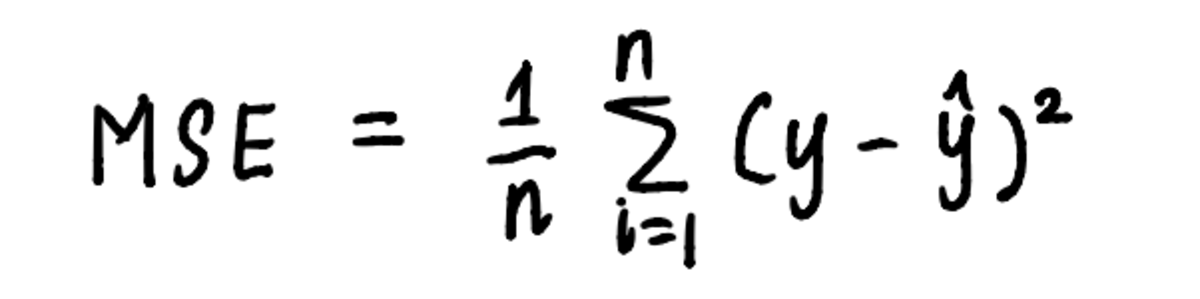
a görbe egyenlete az MSE kiszámításához használt egyenlet

 

És a előző cikk, tudjuk, hogy az egyenlet MSE a mi problémánk a következő:

 

 

Ha kicsinyítünk, láthatjuk, hogy an MSE görbe (amely a mi völgyünkre hasonlít) egy csomó helyettesítéssel megtalálható feltartóztat értékeket a fenti egyenletben. Tehát csatlakoztassuk a 10,000 XNUMX értékét feltartóztat, hogy egy ilyen görbét kapjunk:

 

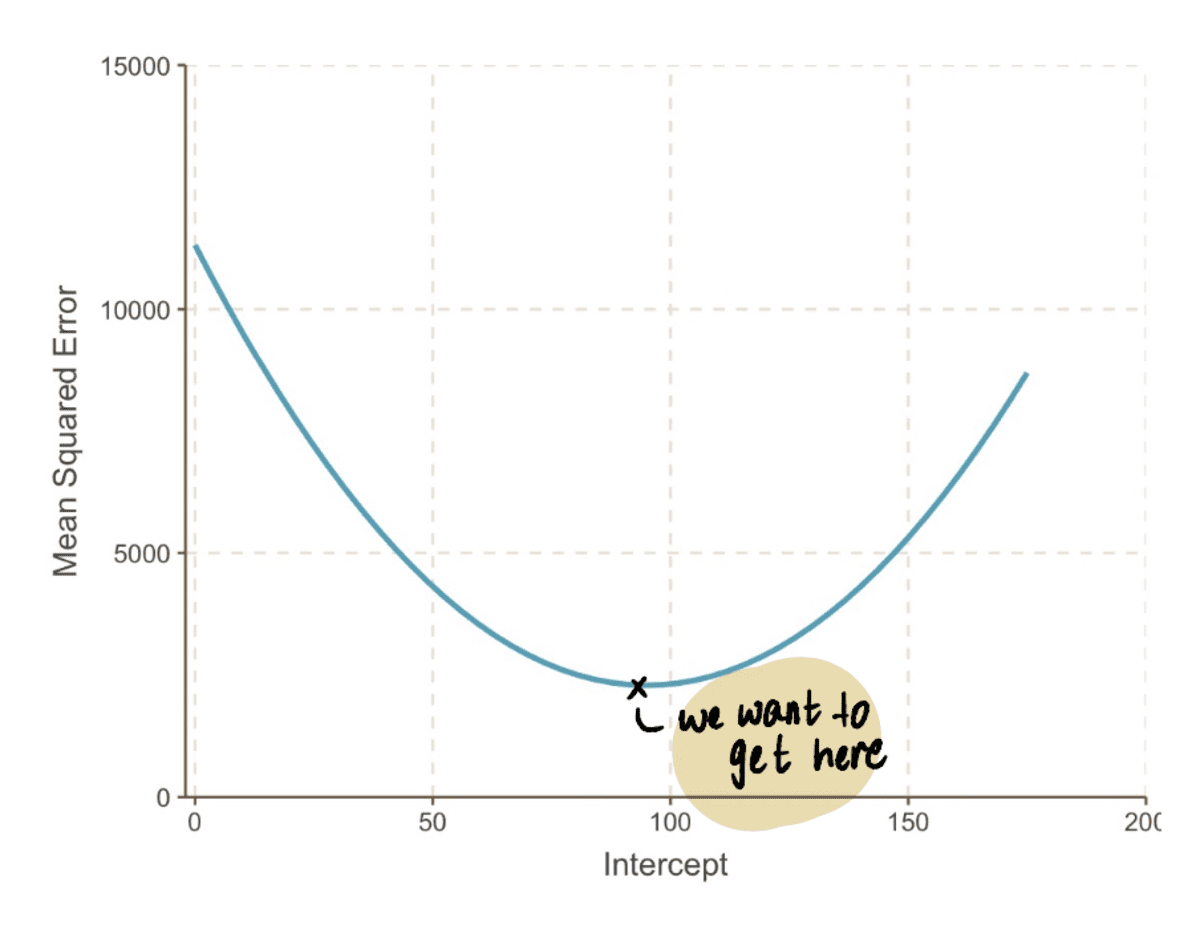
a valóságban nem fogjuk tudni, hogy néz ki az MSE görbe

 

A cél ennek a végére jutni MSE görbe, amit az alábbi lépésekkel tehetünk meg:

1. lépés: Kezdje a fogásérték véletlenszerű kezdeti tippelésével

Ebben az esetben tegyük fel a kezdeti sejtést a feltartóztat értéke 0.

2. lépés: Számítsa ki az MSE görbe gradiensét ezen a ponton

A gradiens Egy görbe egy pontban az érintővonallal van ábrázolva (egy képzeletbeli mondás, hogy az egyenes csak abban a pontban érinti a görbét) abban a pontban. Például az A pontban a gradiens az MSE a görbe a vörös érintővonallal ábrázolható, ha a metszéspont 0.

 

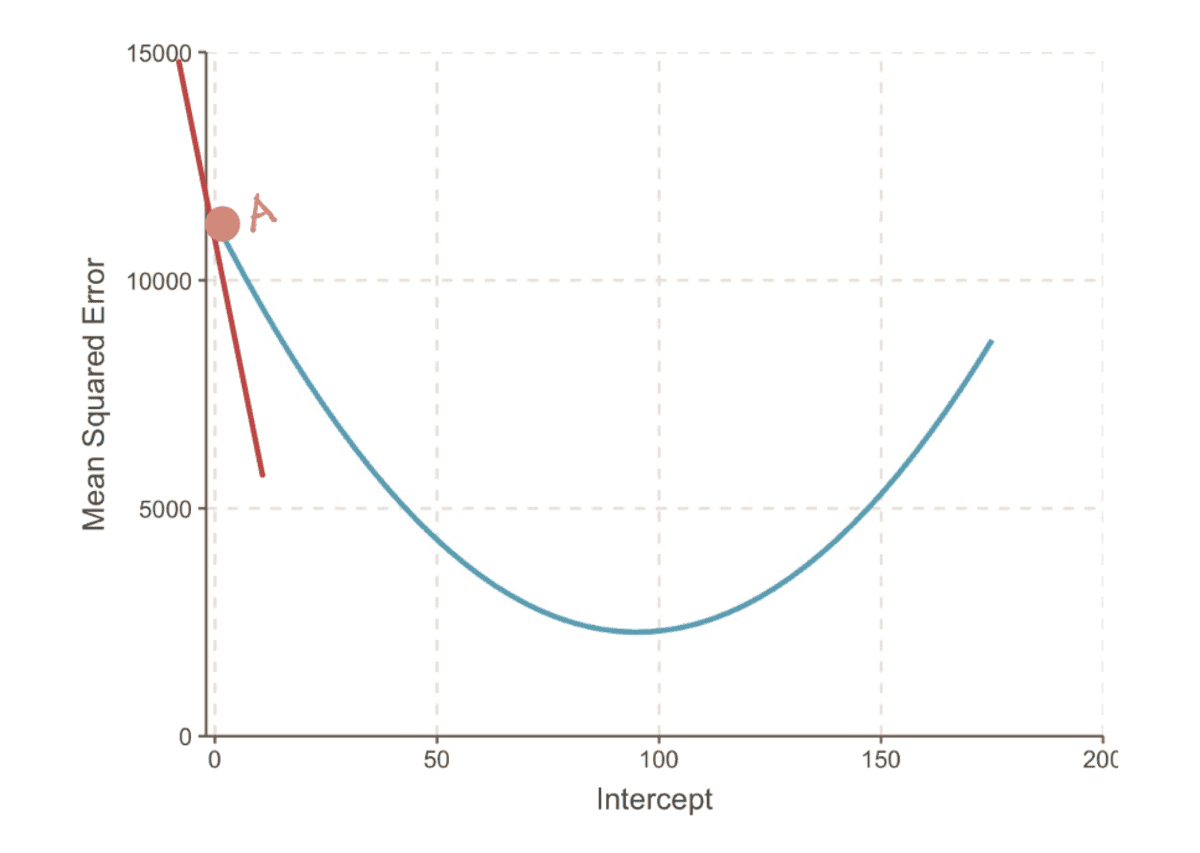
az MSE-görbe gradiense, ha metszéspont = 0

 

Az érték meghatározásához a gradiens, alkalmazzuk a kalkulus ismereteinket. Konkrétan a gradiens egyenlő a görbe deriváltjával feltartóztat egy adott ponton. Ezt a következőképpen jelöljük:

 

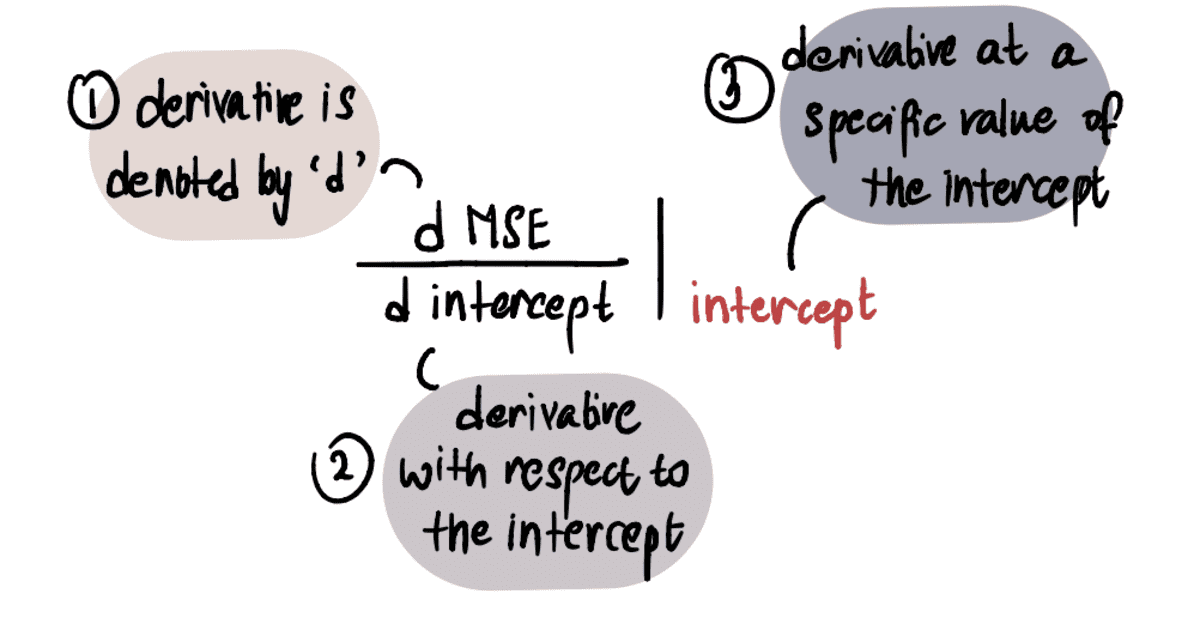
MEGJEGYZÉS: Ha nem ismeri a származékokat, javasoljuk, hogy nézze meg ezt Khan Academy videó ha érdekel. Ellenkező esetben áttekintheti a következő részt, és továbbra is követheti a cikk többi részét.

Kiszámoljuk a az MSE görbe deriváltja az alábbiak szerint:

 

 

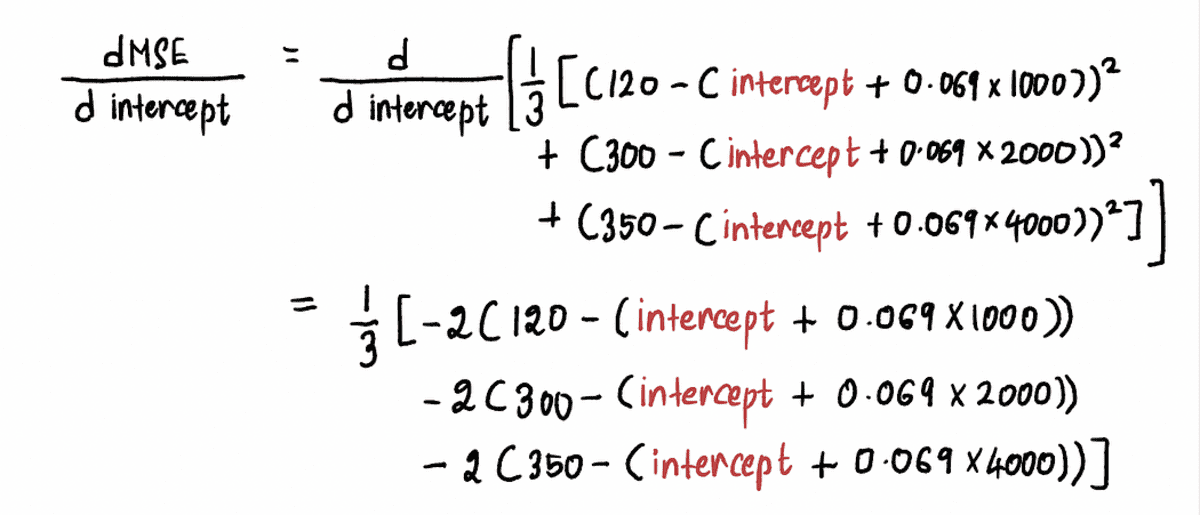
Most, hogy megtalálja a gradiens az A pontban, behelyettesítjük az értékét feltartóztat a fenti egyenlet A pontjában. Mivel feltartóztat = 0, az A pont deriváltja:

 

 

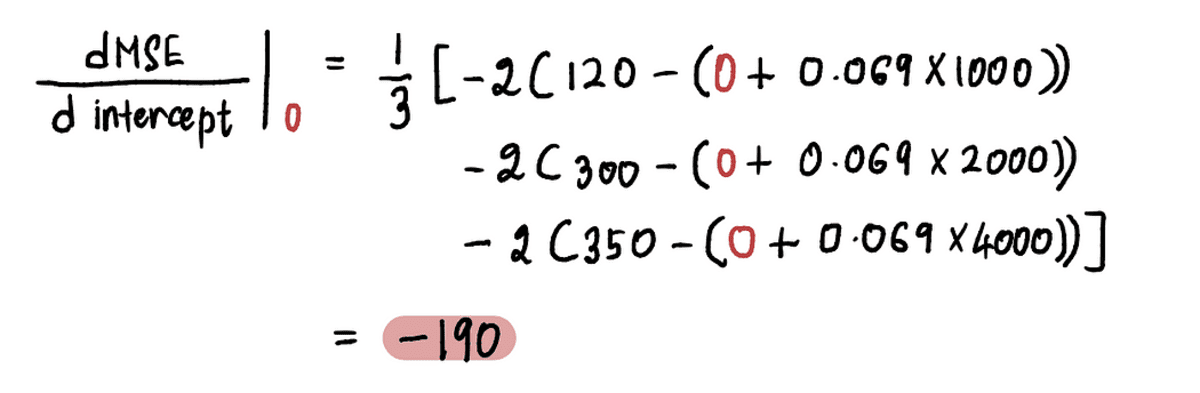
Tehát amikor a feltartóztat = 0, a gradiens = -190

JEGYZET: Ahogy közeledünk az optimális értékhez, a gradiensértékek közelednek a nullához. Az optimális értéknél a gradiens nullával egyenlő. Ezzel szemben minél távolabb vagyunk az optimális értéktől, annál nagyobb lesz a gradiens.

 

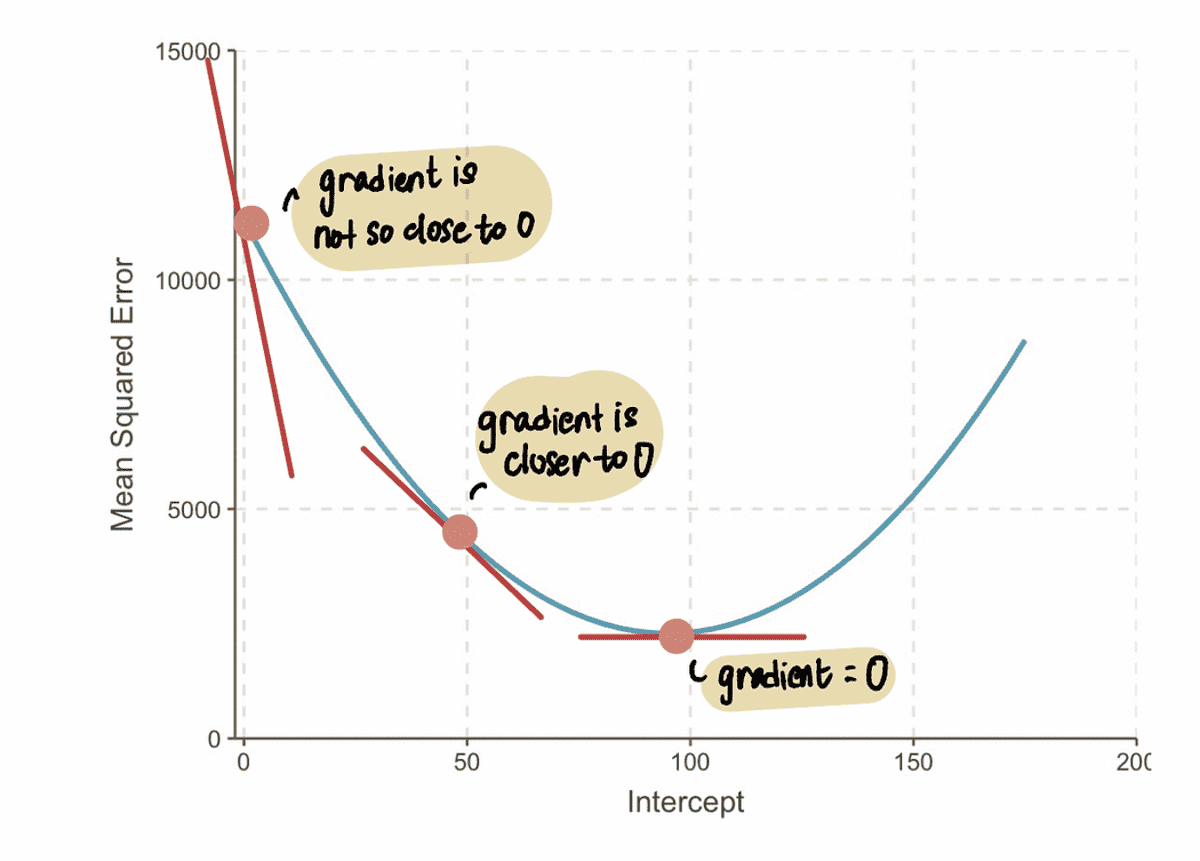
Ebből arra következtethetünk, hogy a lépésméretnek kapcsolódnia kell a gradiens, hiszen megmondja, hogy babalépést vagy nagy lépést tegyünk. Ez azt jelenti, hogy amikor a gradiens A görbe 0-hoz közeli, akkor érdemes babalépéseket tenni, mert közel vagyunk az optimális értékhez. És ha a gradiens nagyobb, nagyobb lépéseket kell tennünk, hogy gyorsabban elérjük az optimális értéket.

JEGYZET: Ha azonban egy szuper nagy lépést teszünk, akkor nagyot ugorhatunk, és kihagyhatjuk az optimális pontot. Tehát óvatosnak kell lennünk.

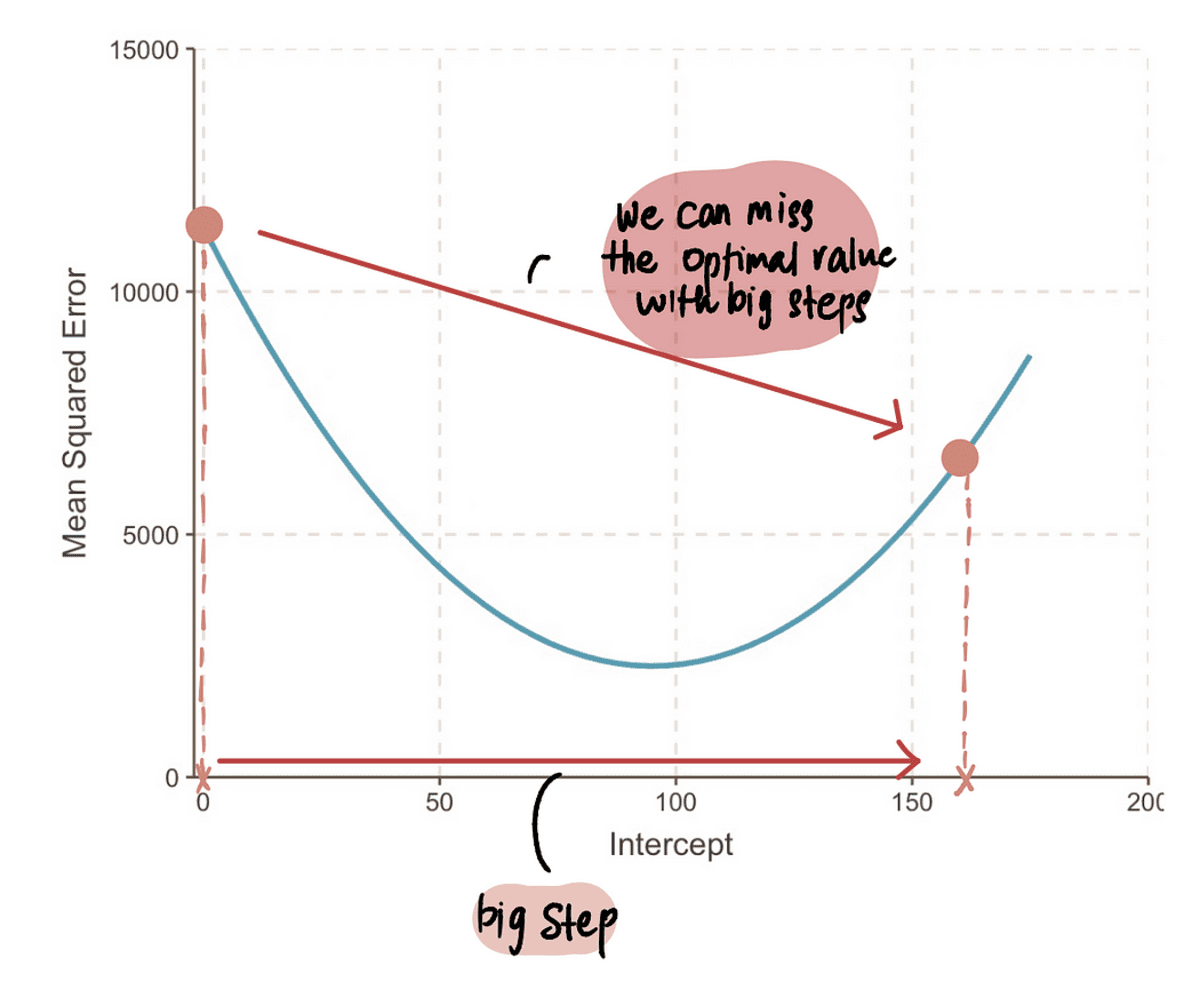
3. lépés: Számítsa ki a lépés méretét a gradiens és a tanulási sebesség segítségével, és frissítse a fogásértéket

Mivel látjuk, hogy a Lépés mérete és a gradiens arányosak egymással, a Lépés mérete szorzatával határozzuk meg gradiens egy előre meghatározott állandó értékkel, amelyet a Tanulási arány:

 

 

A Tanulási arány szabályozza a nagyságát Lépés mérete és biztosítja, hogy a megtett lépés ne legyen túl nagy vagy túl kicsi.

A gyakorlatban a tanulási arány általában egy kis pozitív szám, amely ? 0.001. De a mi problémánkra állítsuk 0.1-re.

Tehát amikor a metszéspont 0, a Lépésméret = gradiens x Tanulási arány = -190*0.1 = -19.

Alapján Lépés mérete fentebb kiszámoltuk, frissítjük a feltartóztat (más néven változtassa meg jelenlegi helyünket) az alábbi egyenértékű képletek bármelyikével:

 

 

Megtalálni az újat feltartóztat ebben a lépésben beillesztjük a megfelelő értékeket…

 

 

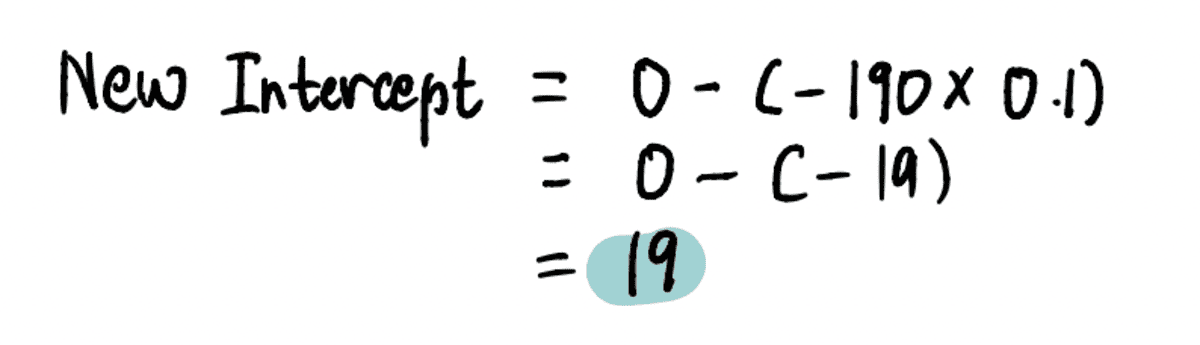
…és találja meg, hogy ez az új feltartóztat = 19.

Most dugja be ezt az értéket a MSE egyenletet, azt találjuk, hogy a MSE amikor a feltartóztat 19 = 8064.095. Észrevesszük, hogy egy nagy lépéssel közelebb kerültünk optimális értékünkhöz és csökkentettük a MSE.

 

 

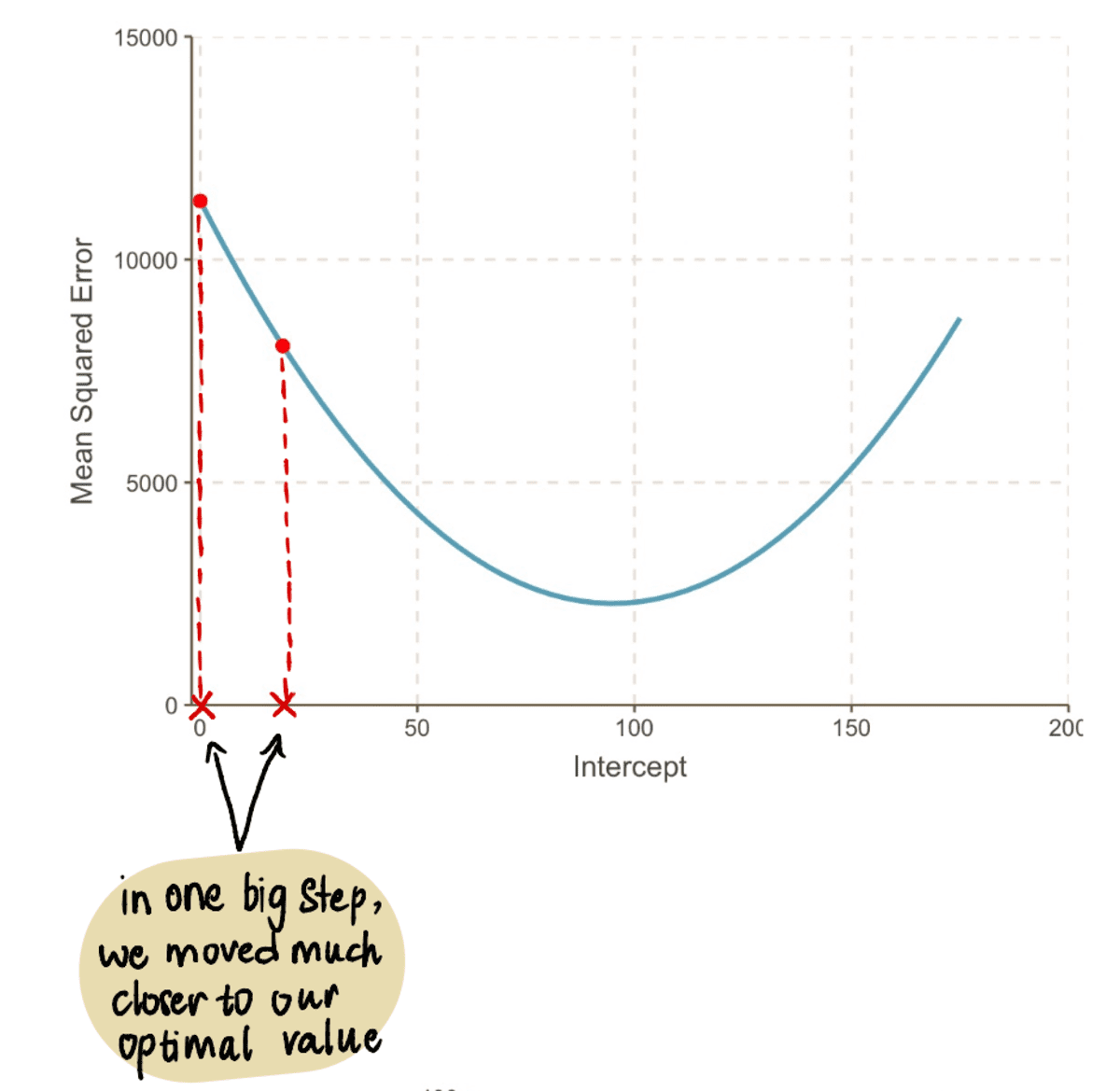
Még ha megnézzük is a grafikonunkat, láthatjuk, mennyivel jobb az új sorunk feltartóztat 19 illeszkedik adatainkhoz, mint a régi sorunkhoz feltartóztat 0:

 

 

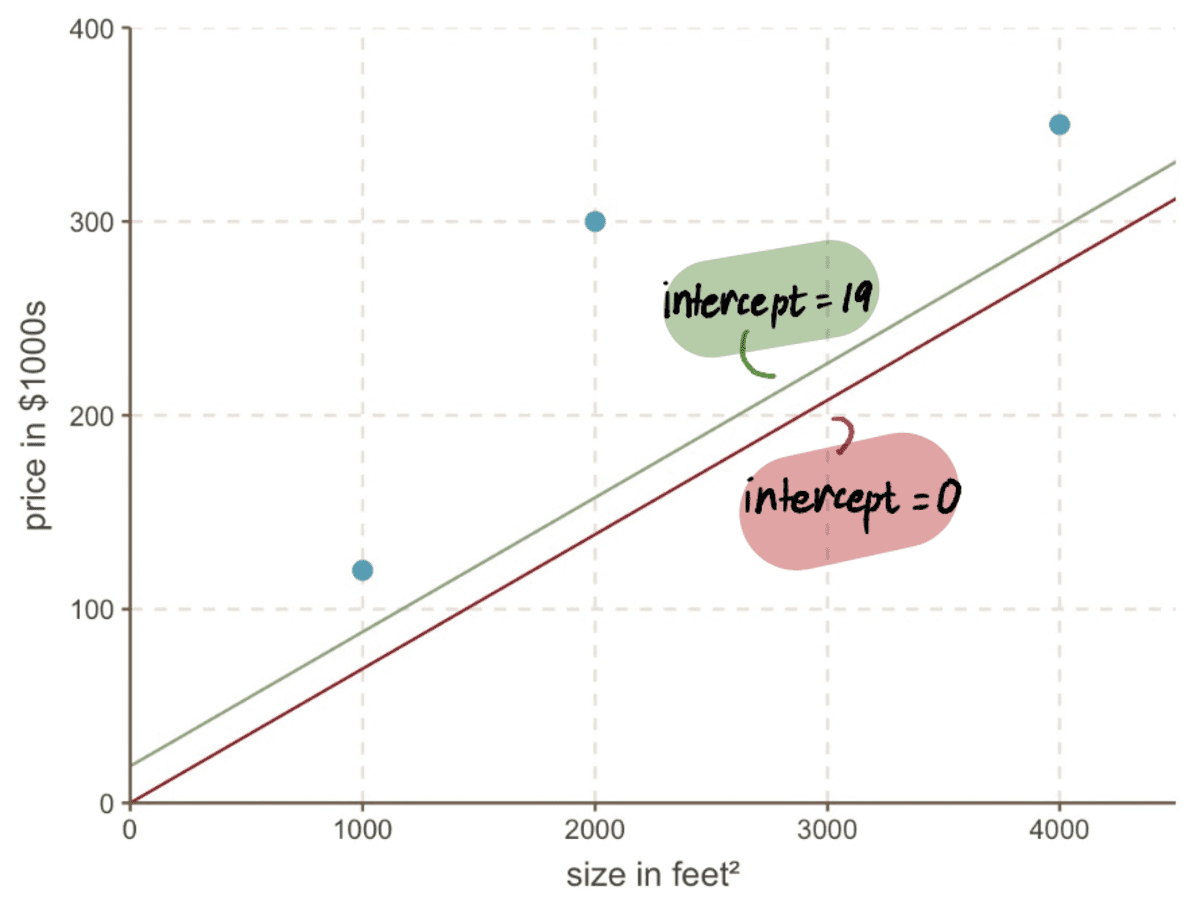
4. lépés: Ismételje meg a 2–3

Megismételjük a 2. és 3. lépést a frissített használatával feltartóztat értéket.

Például mióta az új feltartóztat értéke ebben az iterációban 19, a következő 2 lépés, a gradienst ebben az új pontban számítjuk ki:

 

 

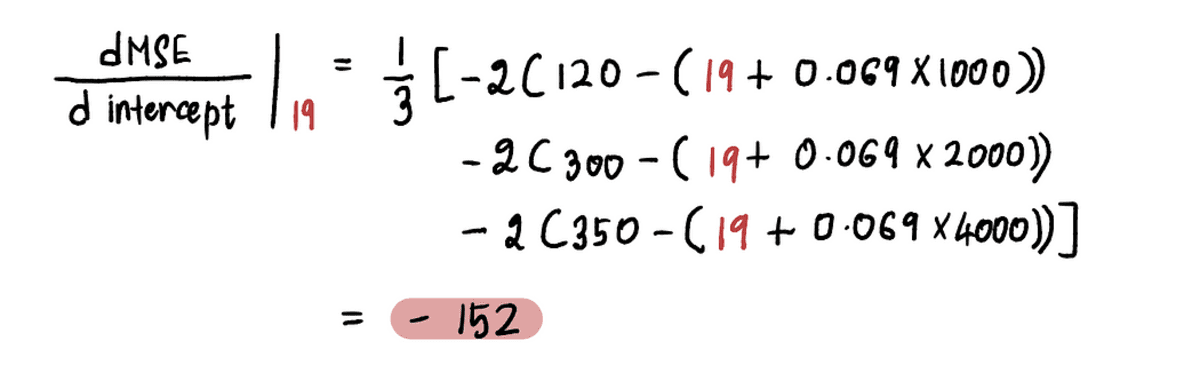
És azt találjuk, hogy a gradiens az MSE görbe a 19 metszéspont értékénél -152 (amint azt a vörös érintővonal ábrázolja az alábbi ábrán).

 

 

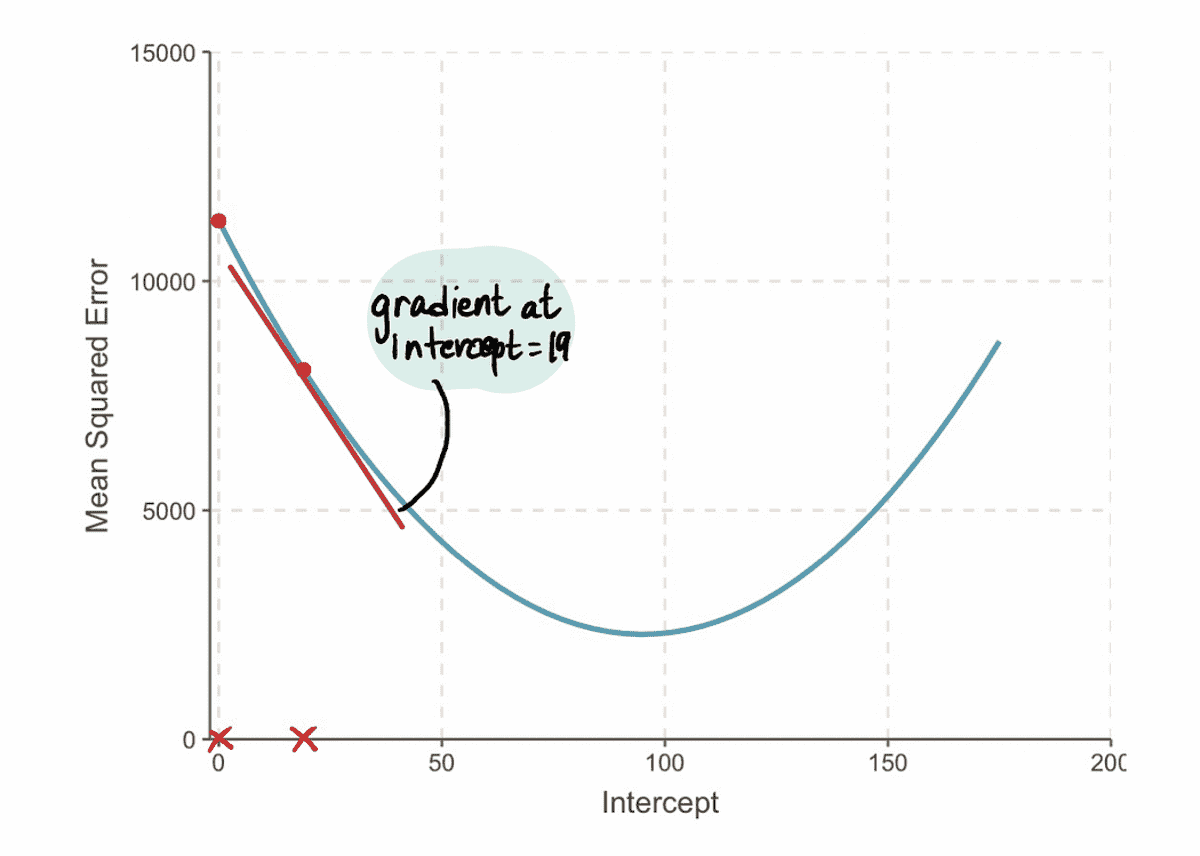
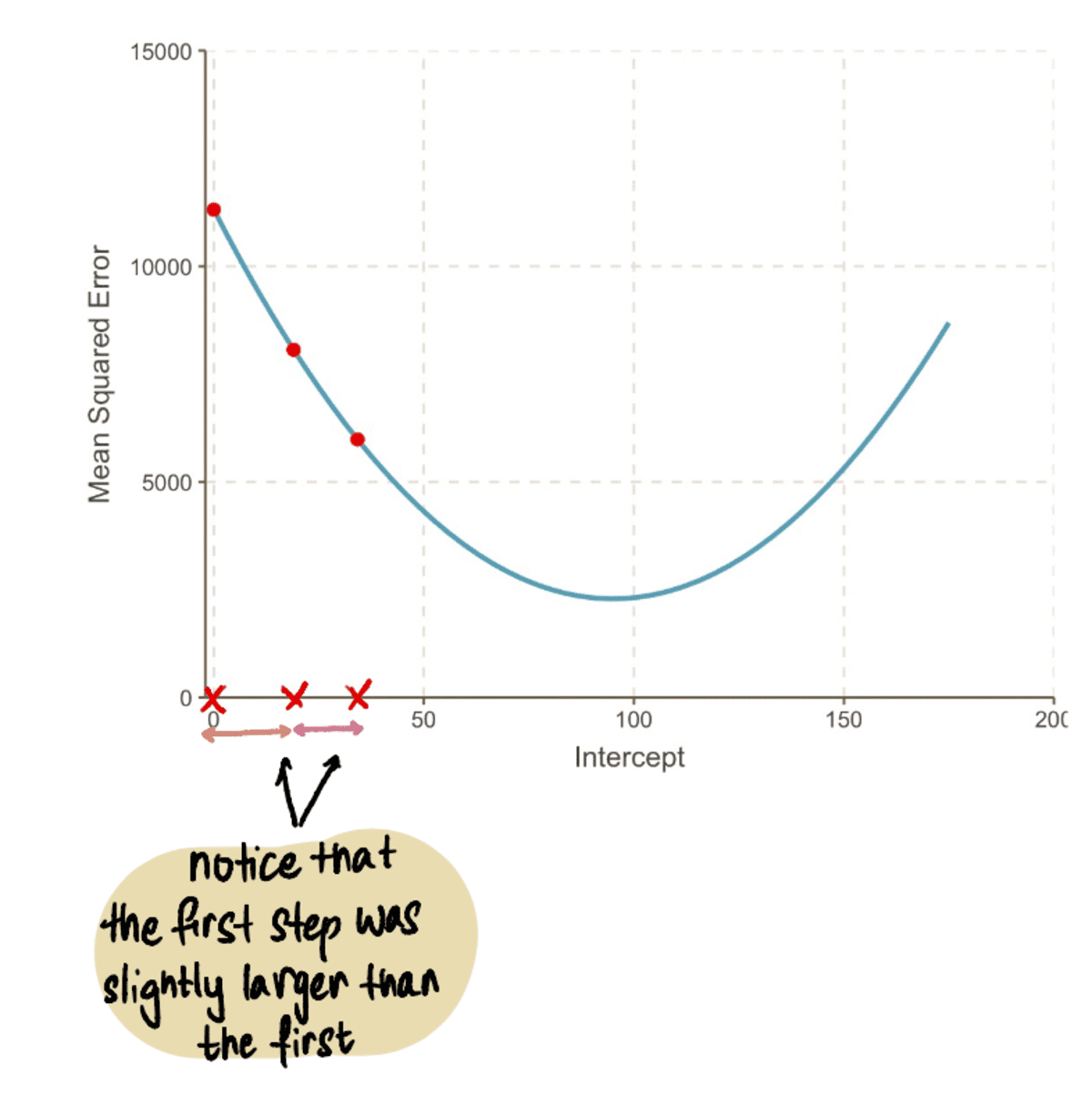
Következő, összhangban 3 lépés, számoljuk ki a Lépés mérete:

 

 

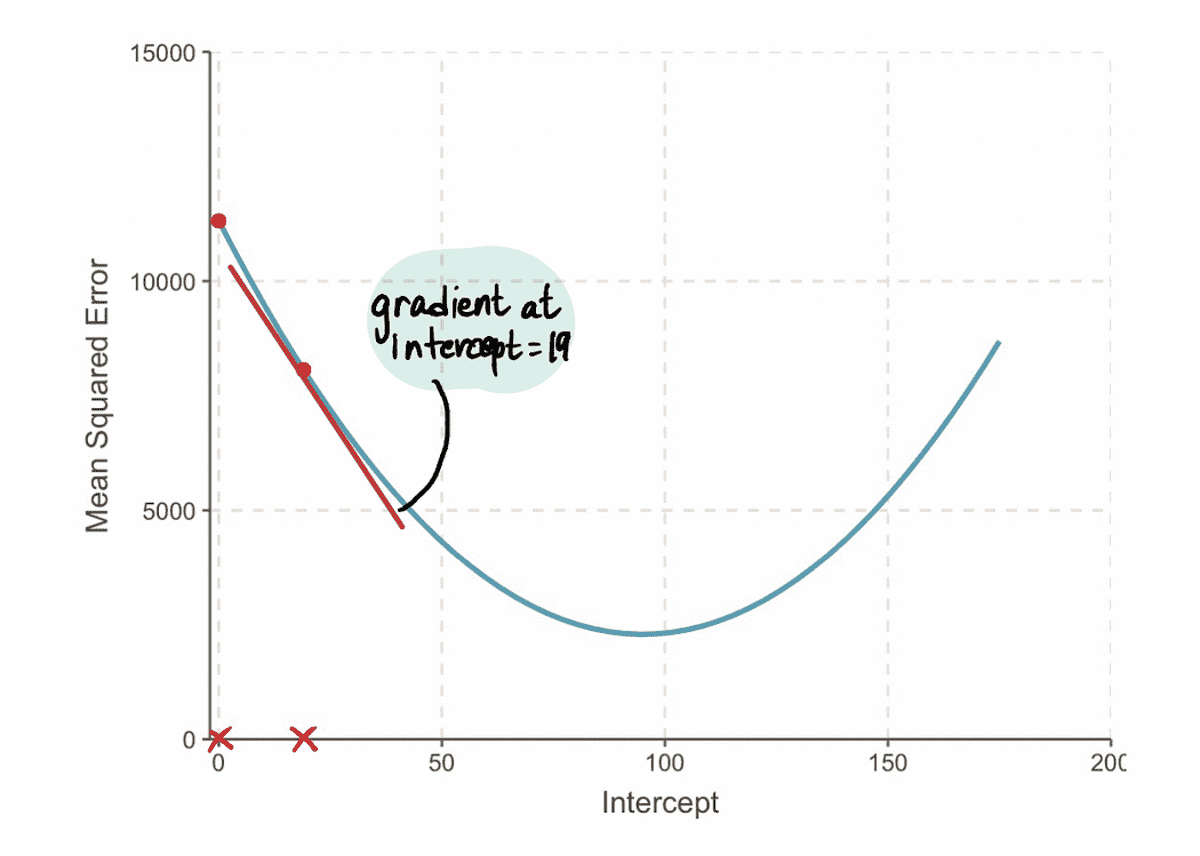
És ezt követően frissítse a feltartóztat érték:

 

 

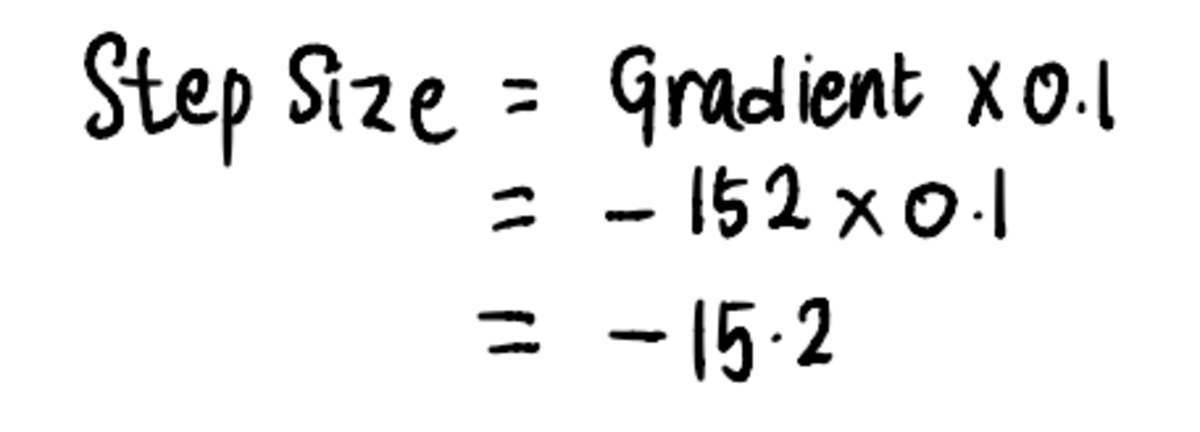
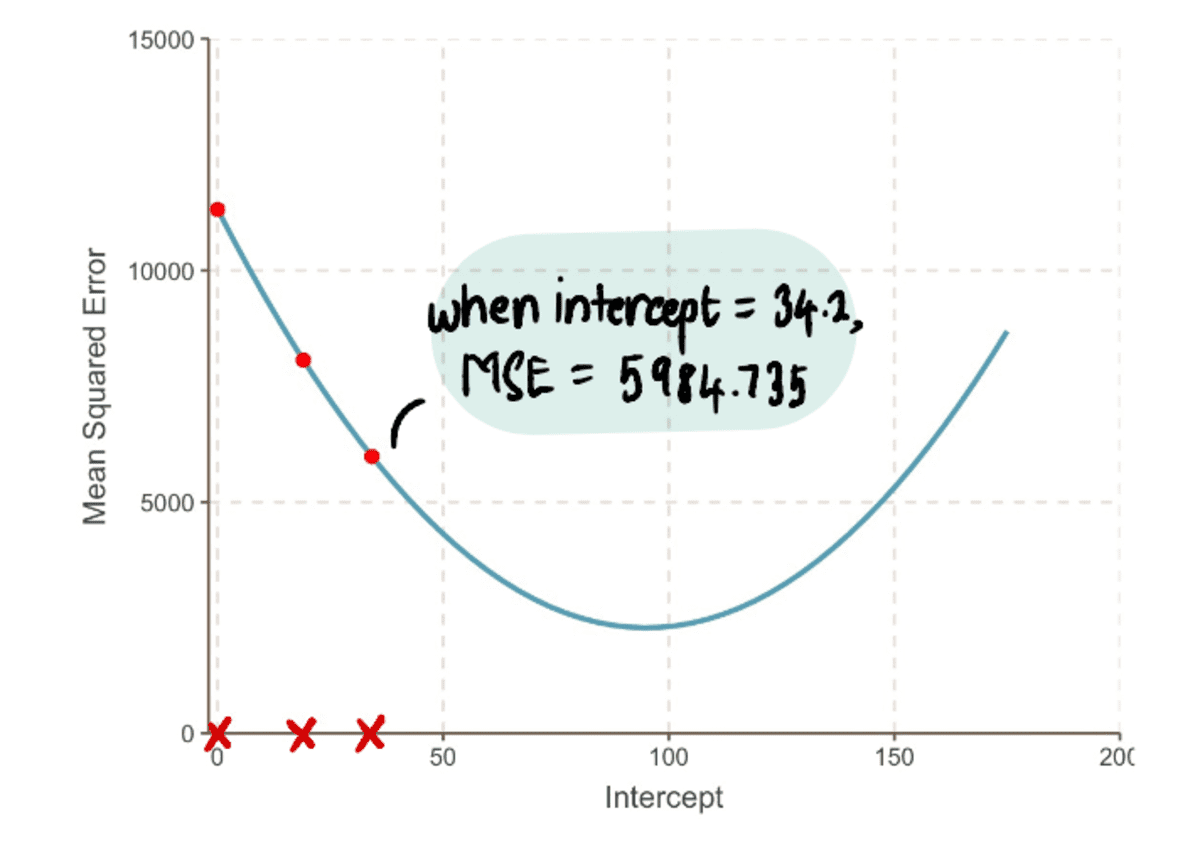
Most összehasonlíthatjuk a sort az előzővel feltartóztat 19-ből az új vonalra az új 34.2-es metszőponttal…

 

 

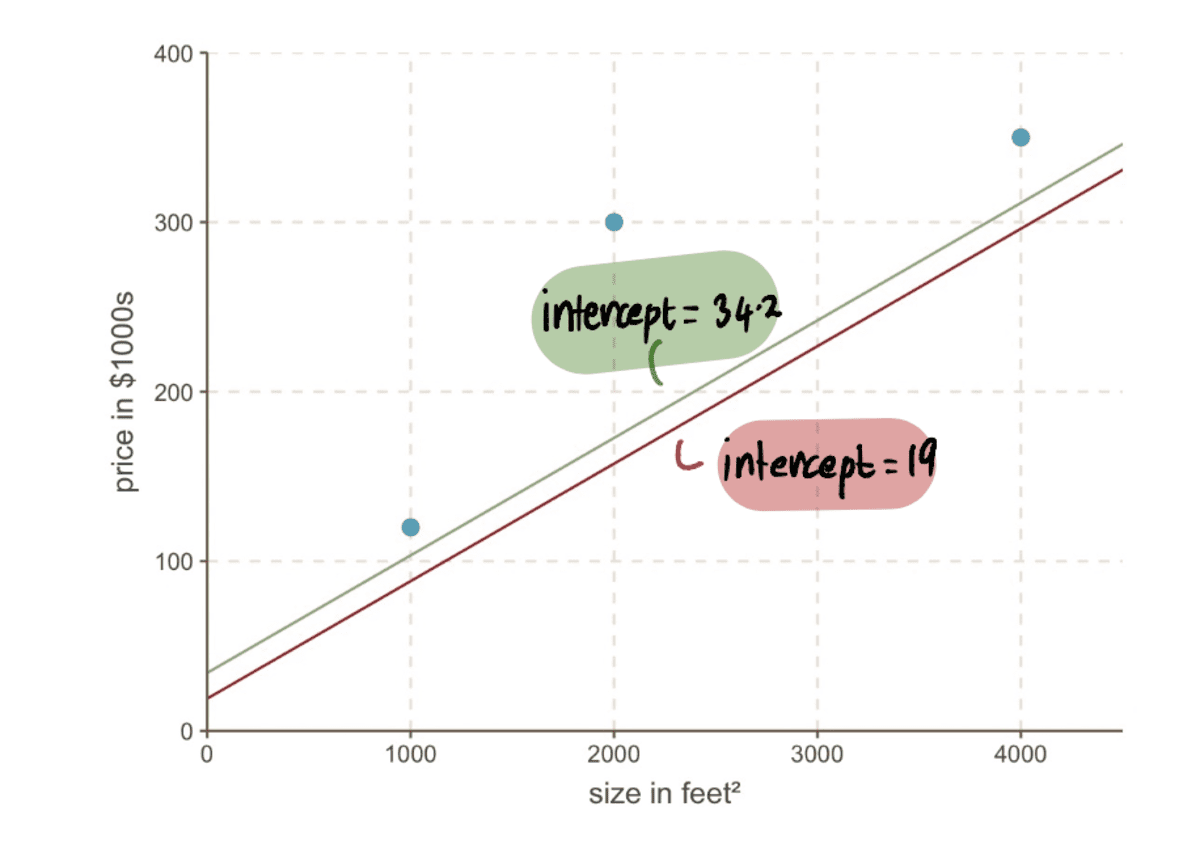
…és láthatjuk, hogy az új sor jobban illeszkedik az adatokhoz.

Összességében, az MSE egyre kisebb…

 

 

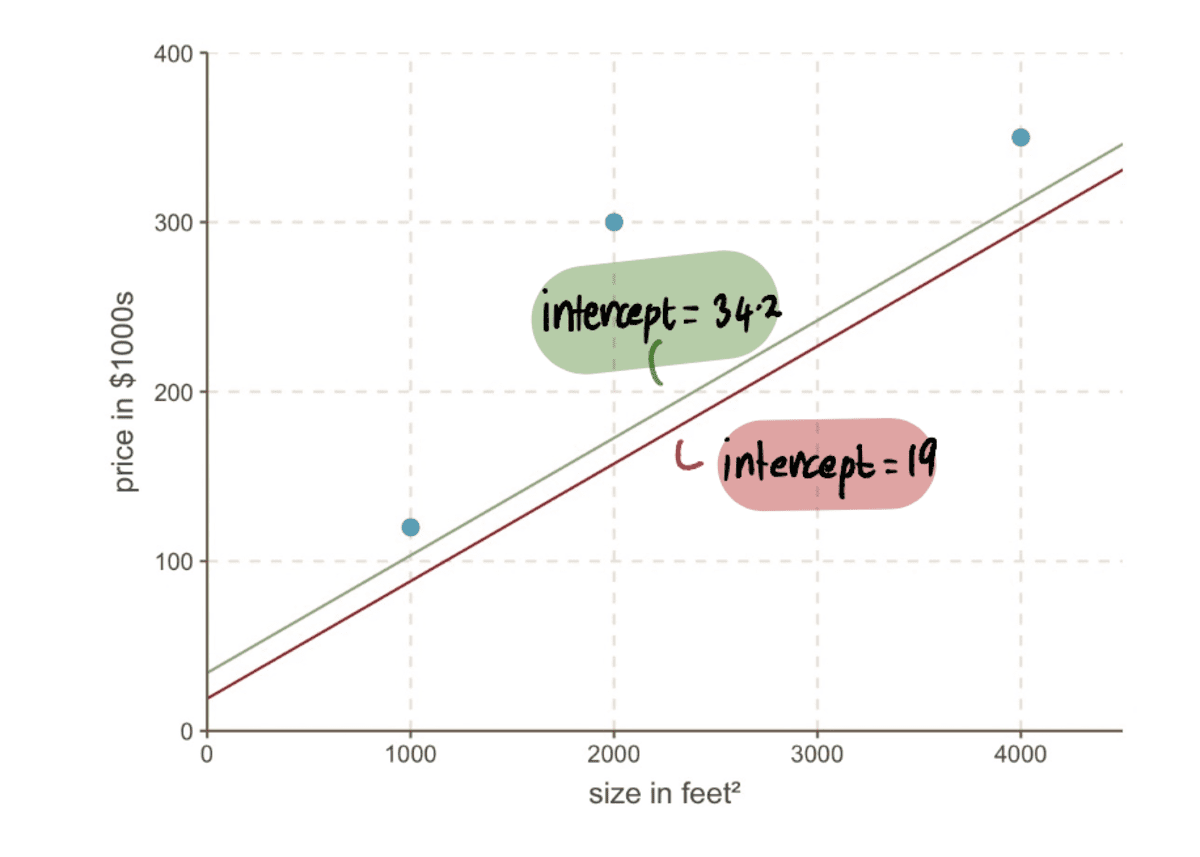
…és a miénk Lépésméretek egyre kisebbek:

 

 

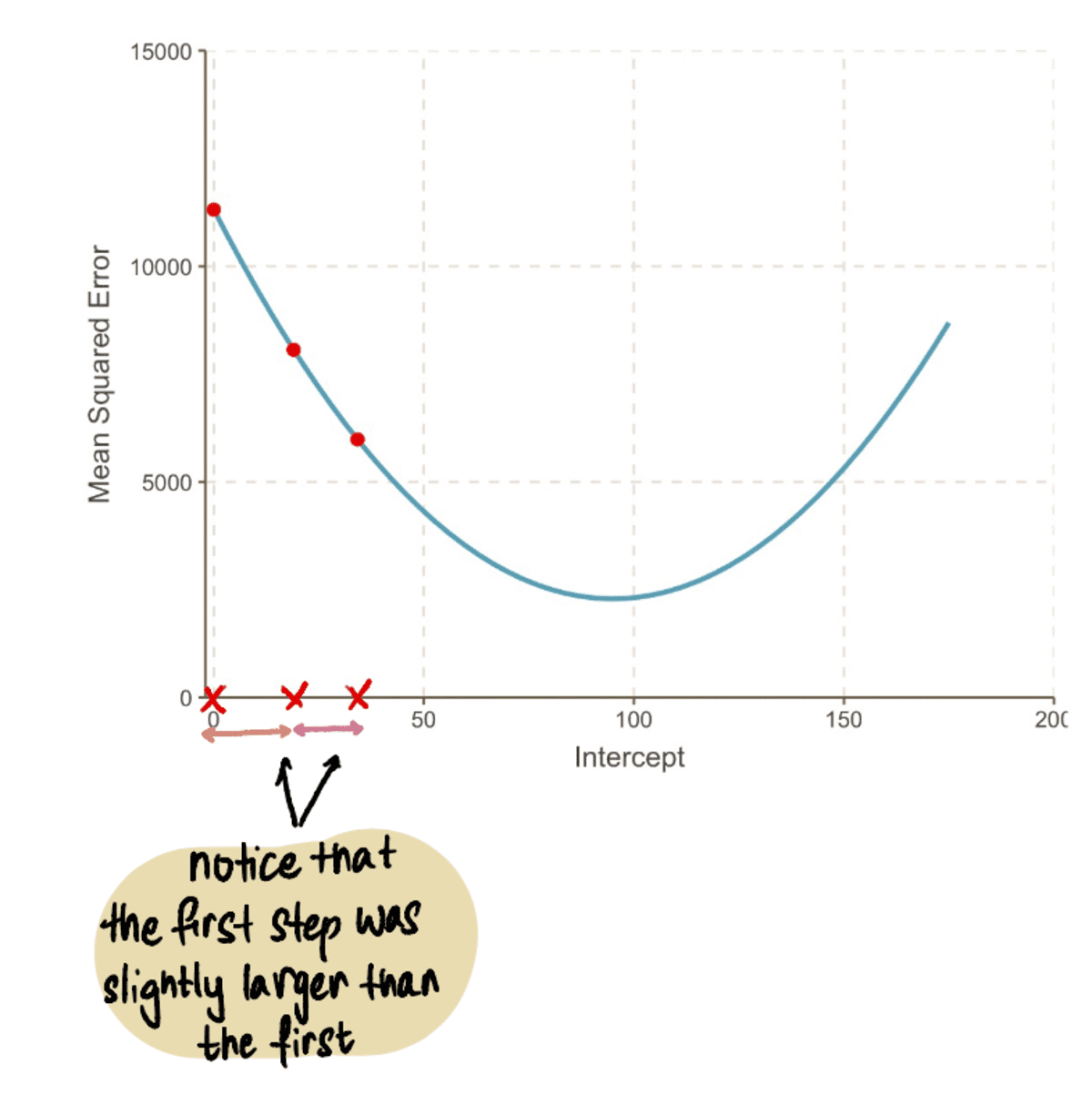
Ezt a folyamatot iteratívan ismételjük, amíg el nem érjük az optimális megoldást:

 

 

Ahogy haladunk a görbe minimumpontja felé, megfigyeljük, hogy a Lépés mérete egyre kisebb lesz. 13 lépés után a gradiens süllyedés algoritmusa megbecsüli a feltartóztat értéke 95. Ha kristálygömbünk lenne, akkor ez a minimum pont lenne MSE ív. És jól látható, hogy ez a módszer mennyire hatékonyabb a brute force megközelítéshez képest, amelyet a előző cikk.

Most, hogy megvan az optimális értékünk feltartóztat, a lineáris regressziós modell a következő:

 

 

És a lineáris regressziós egyenes így néz ki:

 

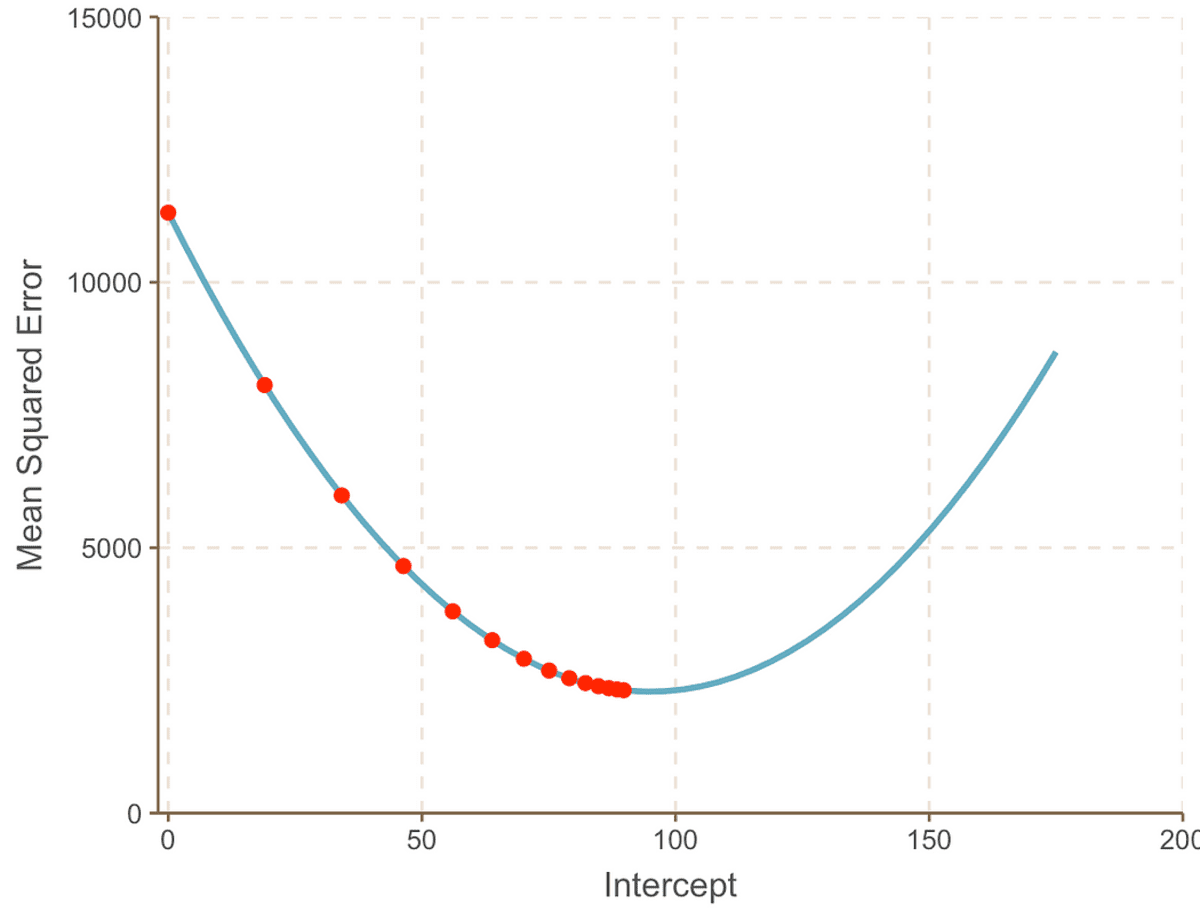
a legjobban illeszkedő egyenes metszésponttal = 95 és meredekséggel = 0.069

 

Végül visszatérve Mark barátunk kérdéséhez – Milyen értékben adja el 2400 láb²-es házát?

 

 

Csatlakoztassa a 2400 láb²-es házat a fenti egyenlethez…

 

 

…és íme. Feleslegesen aggódó barátunknak, Marknak elmondhatjuk, hogy a szomszédságában lévő 3 ház alapján érdemes eladnia házát 260,600 XNUMX dollár körüli áron.

Most, hogy jól ismerjük a fogalmakat, végezzünk egy gyors kérdezz-feleletet, és megválaszoljuk a felmerülő kérdéseket.

Miért működik valójában a gradiens megtalálása?

Ennek szemléltetésére vegyünk egy forgatókönyvet, ahol megpróbáljuk elérni a C görbe minimális pontját, amelyet x*. És jelenleg az A pontban vagyunk x, balra található x*:

 

 

Ha a görbe A pont szerinti deriváltját vesszük figyelembe x, mint dC(x)/dx, negatív értéket kapunk (ez azt jelenti, hogy a gradiens lefelé dől). Azt is megfigyeljük, hogy jobbra kell haladnunk, hogy elérjük x*. Ezért növelnünk kell x hogy elérjük a minimumot x*.

 

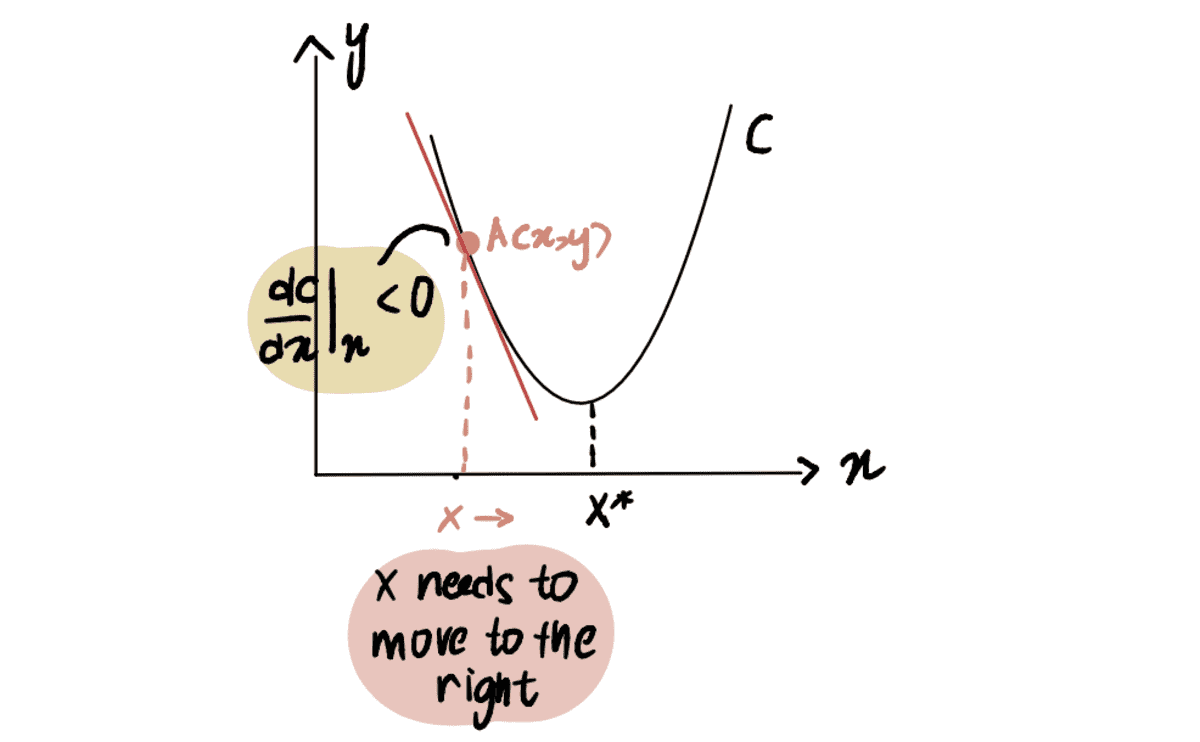
a piros vonal, vagy a gradiens lefelé dől => negatív Gradiens

 
 

Óta dC(x)/dx negatív, x-??*dC(x)/dx nagyobb lesz, mint x, így haladva felé x*.

Hasonlóképpen, ha az A pontban vagyunk az x* minimumponttól jobbra, akkor a-t kapunk pozitív gradiens (gradiens felfelé dől), dC(x)/dx.

 

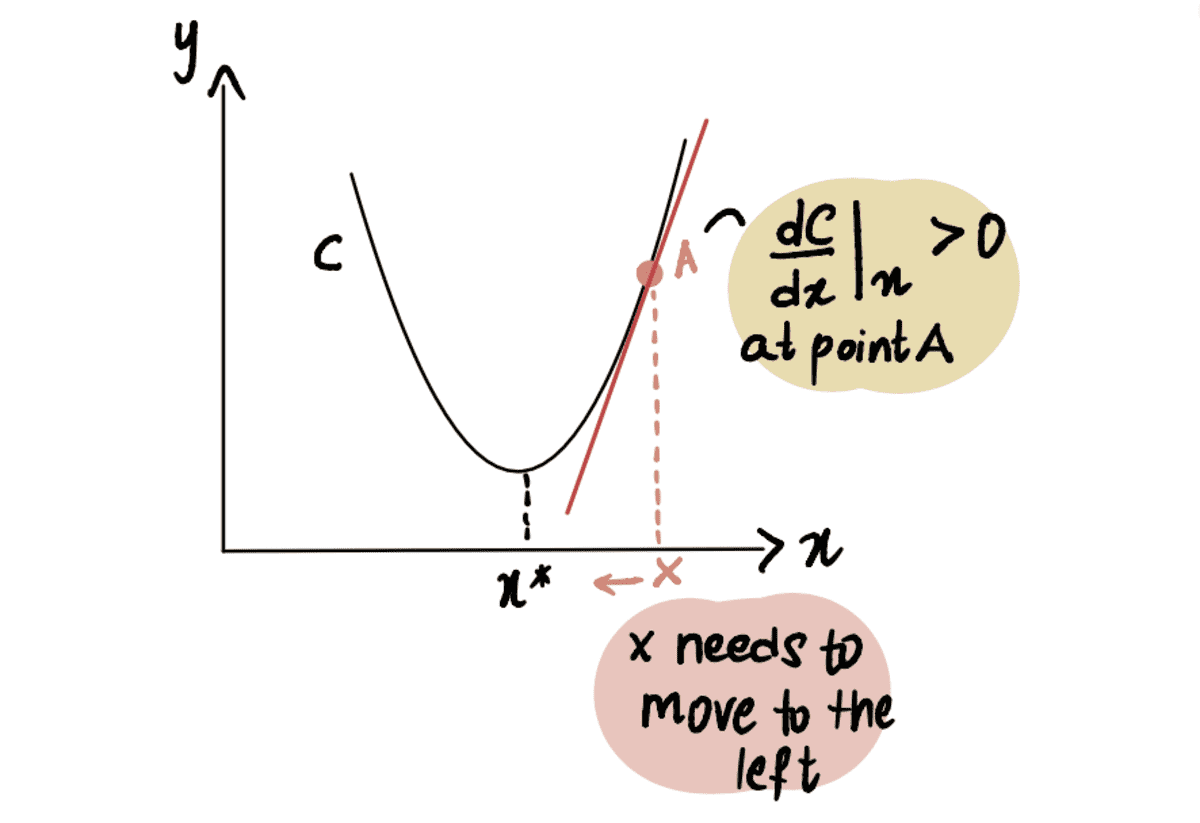
a piros vonal vagy a Gradiens felfelé dől => pozitív Gradiens

 

So x-??*dC(x)/dx kevesebb lesz mint x, így haladva felé x*.

Honnan tudja a gradiens decent, hogy mikor kell abbahagyni a lépések megtételét?

A gradiens süllyedés leáll, amikor a Lépés mérete nagyon közel van a 0-hoz. Amint azt korábban tárgyaltuk, a minimumponton a gradiens 0, és ahogy közeledünk a minimumhoz, a gradiens megközelíti a 0. Ezért amikor a gradiens egy pontban közel van a 0-hoz vagy a minimumpont közelében, a Lépés mérete szintén közel lesz a 0-hoz, jelezve, hogy az algoritmus elérte az optimális megoldást.

 

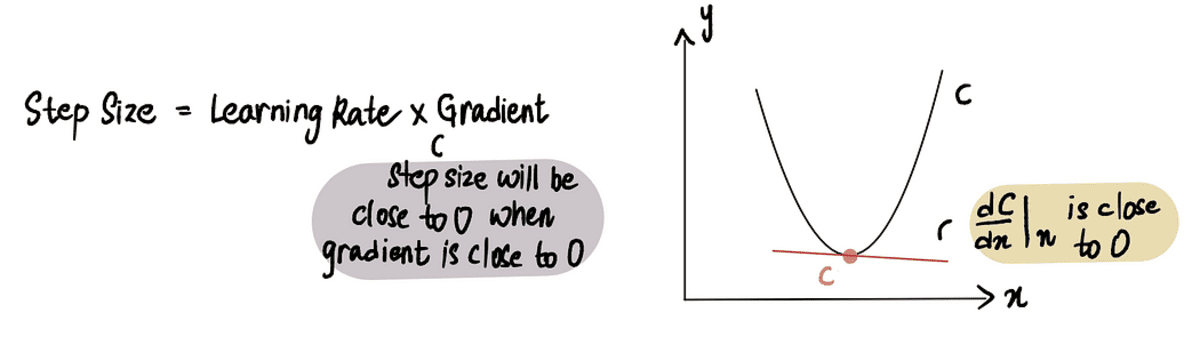
amikor közel vagyunk a minimumponthoz, a gradiens közel 0, és ezt követően a Lépés mérete közel 0

A gyakorlatban a minimális lépésméret = 0.001 vagy kisebb

 

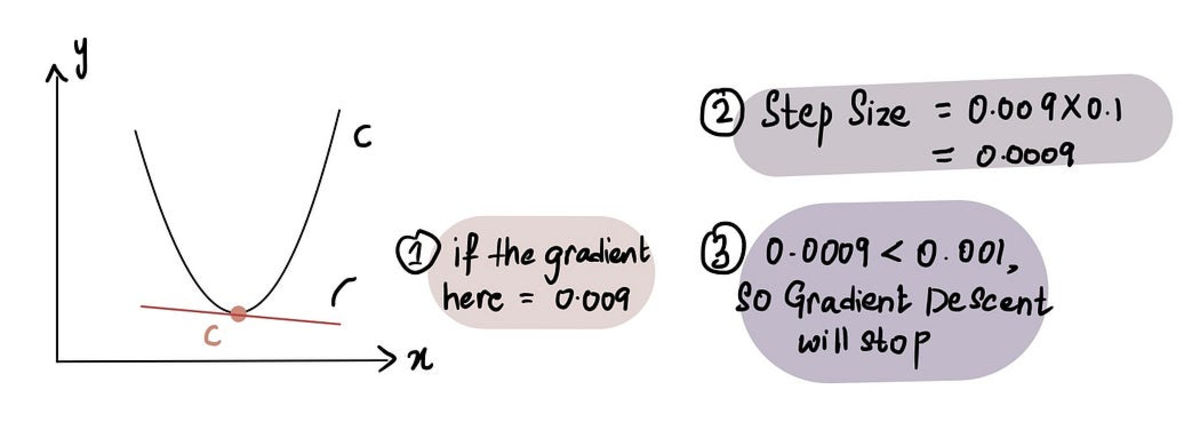
Ennek ellenére a gradiens süllyedés magában foglalja a feladás előtt megtett lépések számának korlátozását is Lépések maximális száma.

A gyakorlatban a lépések maximális száma = 1000 vagy több

Tehát még ha a Lépés mérete nagyobb, mint a Minimális lépésméret, ha több volt, mint a Lépések maximális száma, a gradiens süllyedés leáll.

Mi van, ha a minimumpont azonosítása nehezebb?

Eddig olyan görbével dolgoztunk, ahol könnyen azonosítható a minimumpont (az ilyen görbék ún. domború). De mi van akkor, ha van egy ívünk, ami nem olyan szép (technikailag aka nem domború) és így néz ki:

 

 

Itt láthatjuk, hogy a B pont a globális minimum (tényleges minimum), az A és C pont pedig helyi minimumok (összetéveszthető pontok a globális minimum de nem azok). Tehát ha egy függvénynek több helyi minimumok és egy globális minimum, nem garantált, hogy a gradiens süllyedés megtalálja a globális minimum. Ezen túlmenően, hogy melyik helyi minimumot találja, az a kezdeti találgatás helyzetétől függ (ahogyan az látható: 1 lépés gradiens süllyedés).

 

 

Ha a fenti nem konvex görbét példának vesszük, ha a kezdeti sejtés az A vagy a C blokkban van, a gradiens süllyedés deklarálja, hogy a minimális pont az A vagy C helyi minimumokon van, miközben a valóságban B ponton van. A kezdeti tipp a B blokkban van, az algoritmus megtalálja a B globális minimumot.

A kérdés most az: hogyan lehet jó kezdeti tippet készíteni?

Egyszerű válasz: Próba és hiba. Olyasmi.

Nem túl egyszerű válasz: A fenti grafikonból, ha a minimális sejtésünk a x 0 volt, mivel ez az A blokkban található, ez a helyi minimum A-hoz vezet. Így, amint láthatja, a 0 a legtöbb esetben nem jó kezdeti tipp. Általános gyakorlat, hogy az x összes lehetséges értékének tartományán egyenletes eloszláson alapuló véletlenfüggvényt alkalmaznak. Ezen túlmenően, ha lehetséges, az algoritmus különböző kezdeti találgatásokkal való futtatása és eredményeik összehasonlítása betekintést nyújthat abba, hogy a találgatások jelentősen eltérnek-e egymástól. Ez segít a globális minimum hatékonyabb azonosításában.

Oké, már majdnem ott vagyunk. Utolsó kérdés.

Mi van, ha egynél több optimális értéket keresünk?

Eddig csak az optimális elfogási érték megtalálására koncentráltunk, mert varázsütésre tudtuk a lejtő a lineáris regresszió értéke 0.069. De mi van, ha nincs kristálygömbje, és nem ismeri az optimálisat lejtő érték? Ezután optimalizálnunk kell mind a meredekség, mind a metszéspont értékeit, a következővel kifejezve x? és a x? illetőleg.

Ennek érdekében parciális származékokat kell használnunk az egyszerű származékok helyett.

MEGJEGYZÉS: A részleges származékok kiszámítása ugyanúgy történik, mint a reglar régi származékok, de másképpen jelöljük őket, mert egynél több változónk van, amelyre optimalizálni próbálunk. Ha többet szeretne megtudni róluk, olvassa el ezt cikkben vagy nézd meg ezt videó.

A folyamat azonban viszonylag hasonló marad az egyetlen érték optimalizálásának folyamatához. A költségfüggvény (pl MSE) továbbra is definiálni kell, és a gradiens süllyedés algoritmusát kell alkalmazni, de hozzáadva a parciális derivált mindkét x? és x?.

1. lépés: Adja meg az x₀ és x₁ kezdeti tippjeit

2. lépés: Keresse meg az xXNUMX és xXNUMX parciális deriváltjait ezekben a pontokban

 

 

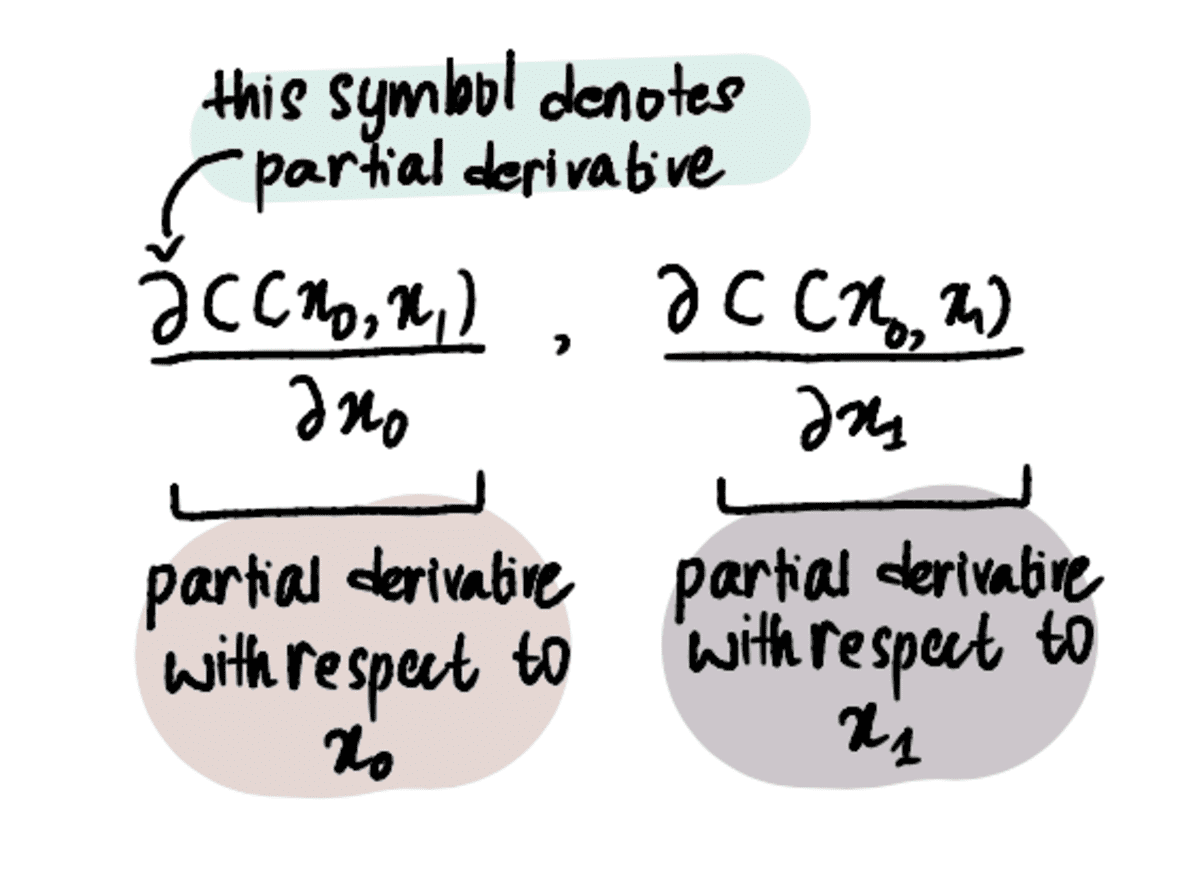
3. lépés: Az x₀ és x₁ egyidejű frissítése a részleges származékok és a tanulási sebesség alapján

 

 

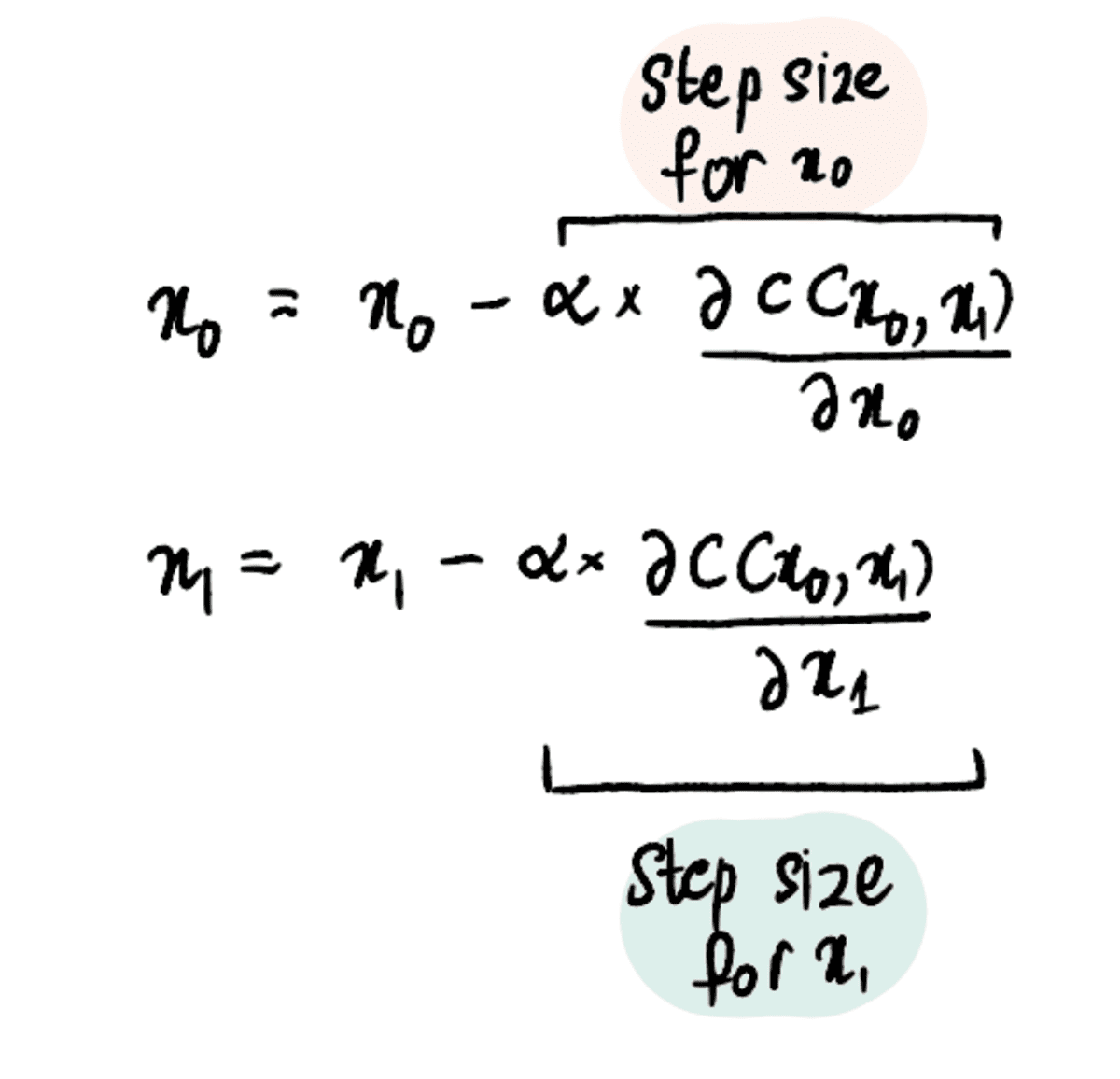
4. lépés: Ismételje meg a 2–3. lépéseket, amíg el nem éri a lépések maximális számát, vagy a lépés mérete kisebb lesz, mint a minimális lépésméret

És ezeket a lépéseket extrapolálhatjuk 3, 4 vagy akár 100 értékre az optimalizáláshoz.

Összefoglalva, a gradiens süllyedés egy hatékony optimalizálási algoritmus, amely segít az optimális érték hatékony elérésében. A gradiens süllyedés algoritmusa sok más optimalizálási problémára is alkalmazható, így az adattudósok alapvető eszköze az arzenáljuk. Irány a nagyobb és jobb algoritmusok most!

 
 
Shreya Rao szemléltesse és magyarázza el a gépi tanulási algoritmusokat laikus kifejezésekkel.

 
eredeti. Engedéllyel újra közzétéve.
 

• SEO által támogatott tartalom és PR terjesztés. Erősödjön még ma.
• Platoblockchain. Web3 metaverzum intelligencia. Felerősített tudás. Hozzáférés itt.
• Forrás: https://www.kdnuggets.com/2023/03/back-basics-part-dos-gradient-descent.html?utm_source=rss&utm_medium=rss&utm_campaign=back-to-basics-part-dos-gradient-descent