Távolságmérők: Euklideszi, Manhattan, Minkowski, Oh My!

A kép szerzője
 

Ha ismeri a gépi tanulást, tudja, hogy az adatkészletben lévő adatpontok és az ezt követően megtervezett jellemzők mind pontok (vagy vektorok) egy n-dimenziós térben.

Bármely két pont távolsága is megragadja a köztük lévő hasonlóságot. A felügyelt tanulási algoritmusok, mint például a K Nearest Neighbors (KNN) és a klaszterező algoritmusok, mint a K-Means Clustering a távolságmérők hogy megörökítse a hasonlóság adatpontok között. 

A klaszterezés során a kiértékelt távolságmérőt az adatpontok csoportosítására használják. Míg a  KNN-ben ezt a távolságmérőt használják az adott adatponthoz legközelebbi K pont megkeresésére.

Ebben a cikkben áttekintjük a távolságmérők tulajdonságait, majd megvizsgáljuk a leggyakrabban használt távolságmérőket: Euklideszi, Manhattan és Minkowski. Ezután kitérünk arra, hogyan lehet ezeket Pythonban kiszámítani a scipy modul beépített függvényei segítségével.

Kezdjük!

Mielőtt megismerkednénk a különböző távolságmérőkkel, tekintsük át azokat a tulajdonságokat, amelyeknek egy metrikus térben lévő távolságmérőknek meg kell felelniük [1]:

1. Szimmetria 

If x és a y két pont egy metrikus térben, akkor a távolság  x és a y közötti távolságnak kell lennie  y és a x.

2. Nem negativitás 

A távolságok mindig ne legyenek negatívak. Ez azt jelenti, hogy nullánál nagyobbnak vagy egyenlőnek kell lennie.

A fenti egyenlőtlenség érvényes a (d(x,y) = 0) akkor és csak akkor  x és a y ugyanazt a pontot jelöli, pl. x = y.

3. Háromszög egyenlőtlenség 

Adott három pont x, yés z, a távolságmérőnek ki kell elégítenie a háromszög egyenlőtlenséget: 

Az euklideszi távolság a legrövidebb távolság a metrikus tér bármely két pontja között. Vegye figyelembe két pontot x és a y egy kétdimenziós síkban (x1, x2) és (y1, y2) koordinátákkal.

Az euklideszi távolság között x és a y megmutatva:

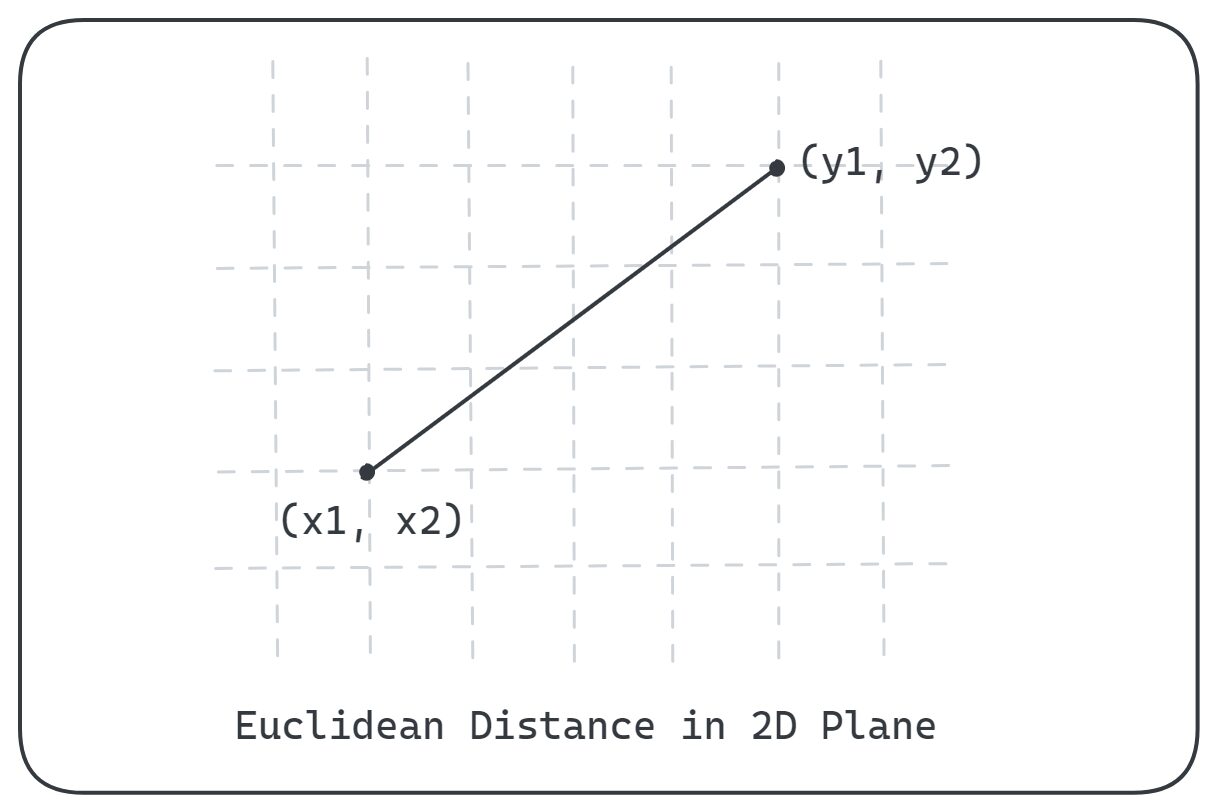
A kép szerzője
 

Ezt a távolságot a két pont megfelelő koordinátái közötti különbségek négyzetes összegének négyzetgyöke adja meg. Matematikailag a pontok közötti euklideszi távolság x és a y kétdimenziós síkban a következő képlet adja meg:

N méretre kiterjesztve a pontokat x és a y formájúak x = (x1, x2, …, xn) és y = (y1, y2, …, yn), a következő egyenletünk van az euklideszi távolságra:

Az euklideszi távolság kiszámítása Pythonban

Az euklideszi távolság és a cikkben szereplő egyéb távolságmérők a kényelmi függvények segítségével számíthatók ki a térbeli modul a SciPy-ben.

Első lépésként importáljunk distance a Scipy-től spatial modul:

from scipy.spatial import distance

Ezután inicializálunk két pontot x és a y így:

x = [3,6,9]
y = [1,0,1]

Használhatjuk a euclidean kényelmi függvény a pontok közötti euklideszi távolság meghatározásához x és a y:

print(distance.euclidean(x,y))
Output >> 10.198039027185569

A Manhattan távolság, más néven taxi távolság ill várostömb távolság, egy másik népszerű távolságmérő. Tegyük fel, hogy egy kétdimenziós síkon belül van, és csak a tengelyek mentén mozoghat, ahogy az ábra mutatja:

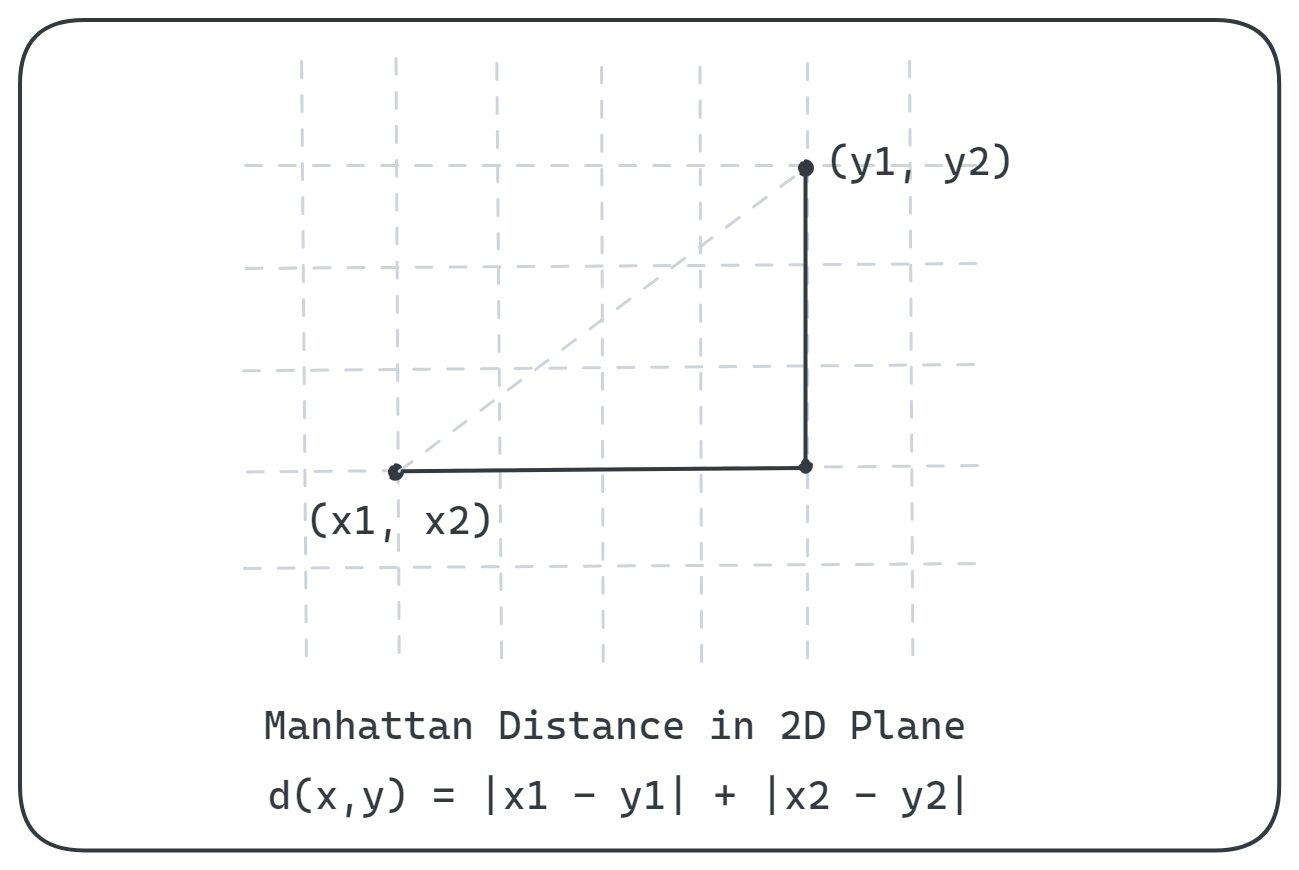
A kép szerzője
 

A pontok közötti manhattani távolság x és a y által adva:

Az n-dimenziós térben, ahol minden pontnak n koordinátája van, a Manhattan távolságot a következő képlet adja meg:

Bár a Manhattan távolság nem adja meg a legrövidebb távolságot két adott pont között, gyakran előnyben részesítik olyan alkalmazásokban, ahol a jellemzőpontok nagy dimenziós térben helyezkednek el [3].

Manhattan távolság kiszámítása Pythonban

Megtartjuk az előző példában szereplő importot, valamint x és y értéket:

from scipy.spatial import distance x = [3,6,9]
y = [1,0,1]

A Manhattan (vagy várostömb) távolság kiszámításához használhatjuk a cityblock funkció:

print(distance.cityblock(x,y))
Output >> 16

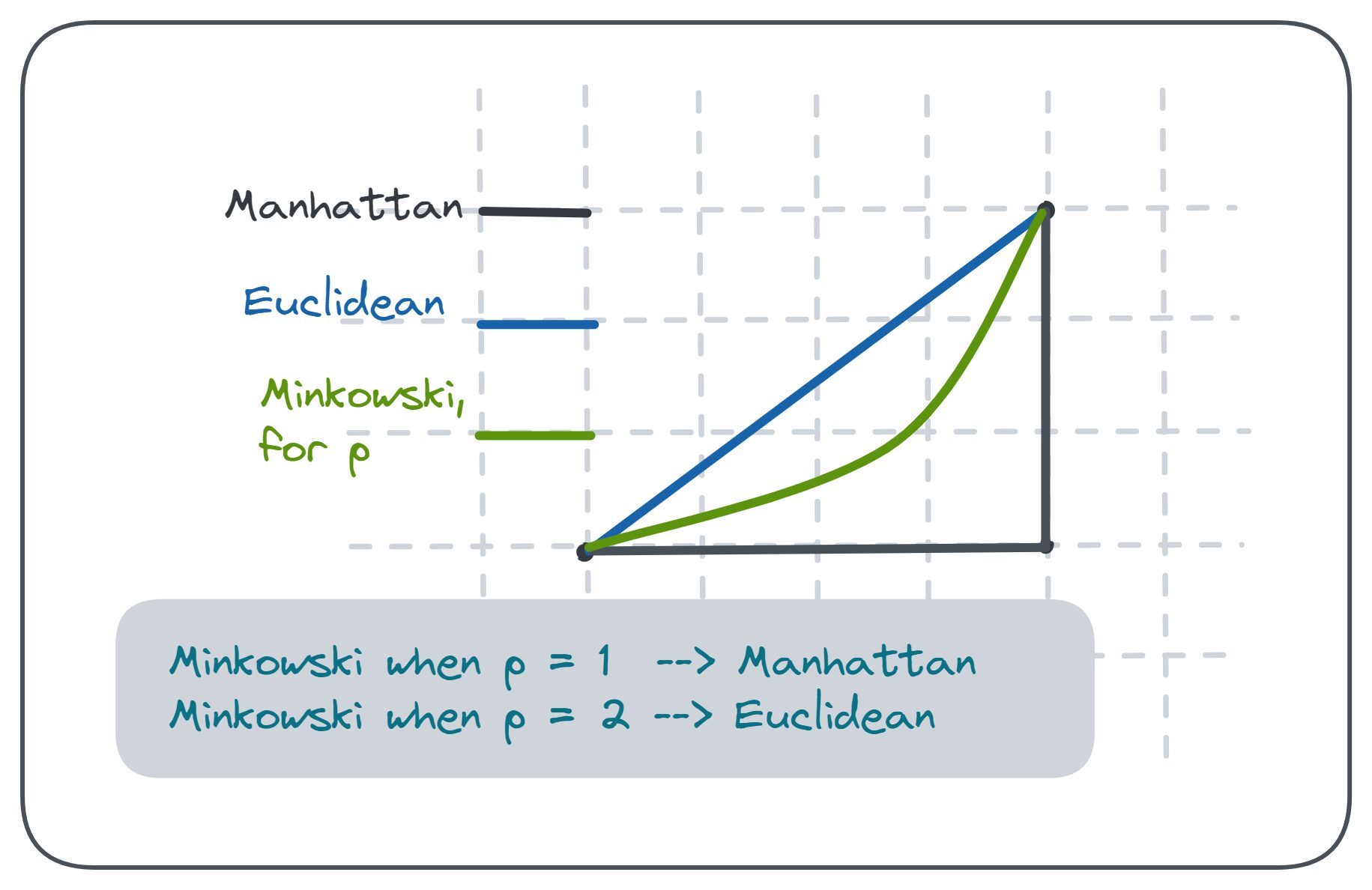
A német matematikusról, Hermann Minkowskiról [2] elnevezett Minkowski-távolság egy normált vektortérben a következőképpen adódik:

Ezt elég egyértelmű belátni p = 1, a Minkowski távolságegyenlet ugyanazt a formát ölti, mint a Manhattan távolság egyenlete:

Hasonlóképpen a p = 2, a Minkowski-távolság megegyezik az euklideszi távolsággal:

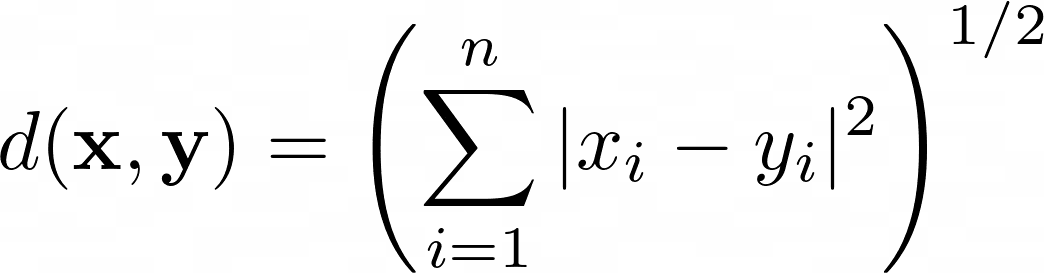
Minkowski távolság kiszámítása Pythonban

Számítsuk ki a pontok közötti Minkowski-távolságot x és a y:

from scipy.spatial import distance x = [3,6,9]
y = [1,0,1]

Azon pontokon (tömbökön) kívül, amelyek között a távolságot ki kell számítani, a minkowski A távolság kiszámítására szolgáló függvény is beveszi a paramétert p: 

print(distance.minkowski(x,y,p=3))
Output >> 9.028714870948003

Annak ellenőrzésére, hogy a Minkowski-távolság Manhattan-távolságra számít-e p =1 esetén, hívjuk fel minkowski funkcióval p 1-re állítva:

print(distance.minkowski(x,y,p=1))
Output >> 16.0

Ellenőrizzük azt is, hogy a Minkowski-távolság p = 2 esetén a korábban kiszámított euklideszi távolságra kerül-e:

print(distance.minkowski(x,y,p=2))
Output >> 10.198039027185569

És ez egy pakolás! Ha ismeri a normált vektortereket, látnia kell a hasonlóságot az itt tárgyalt távolságmérők és az Lp-normák között. Az euklideszi, manhattani és minkowski távolságok ekvivalensek a különbségvektor L2, L1 és Lp normáival egy normált vektortérben. 

Ennyi az oktatóanyaghoz. Remélem, most már rájött a közös távolságmérőkre. Következő lépésként megpróbálhatja eljátszani a különböző tanult mérőszámokat, amikor legközelebb gépi tanulási algoritmusokat tanít. 

Ha szeretné elkezdeni az adattudományt, nézze meg ezt a la GitHub adattárak egyike az adattudomány tanulására. Boldog tanulást!

[1] Metrikus terek, Wolfram Mathworld

[2] Minkowski távolság, Wikipédia 

[3] A távolságmérők meglepő viselkedéséről a nagy dimenziós térbenCC Agarwal et al.

[4] SciPy távolságfüggvények, SciPy Docs
 
 
Bala Priya C egy műszaki író, aki szeret hosszú formátumú tartalmat készíteni. Érdeklődési területe a matematika, a programozás és az adattudomány. Tanulmányait megosztja a fejlesztői közösséggel oktatóanyagok, használati útmutatók és egyebek készítésével.

• SEO által támogatott tartalom és PR terjesztés. Erősödjön még ma.
• Platoblockchain. Web3 metaverzum intelligencia. Felerősített tudás. Hozzáférés itt.
• Forrás: https://www.kdnuggets.com/2023/03/distance-metrics-euclidean-manhattan-minkowski-oh.html?utm_source=rss&utm_medium=rss&utm_campaign=distance-metrics-euclidean-manhattan-minkowski-oh-my