A bizalmi intervallumok megértése Python segítségével

Ez a cikk részeként jelent meg Adattudományi Blogaton.

Tartalomjegyzék

1. Bevezetés
2. Konfidencia intervallumok Z-statisztikával
3. A bizalmi intervallumok értelmezése
4. A z-statisztikát használó CI-re vonatkozó feltevések
5. Konfidencia intervallumok t-statisztikával
6. Feltételezések a CI-re t-statisztika segítségével
7. T-intervallum készítése párosított adatokkal
8. z-érték vs t-érték: mikor mit kell használni?
9. Bizalmi intervallumok a pythonnal
10. End-Note

Bevezetés

Amikor egy statisztikai problémát megoldunk, aggodalomra ad okot a populációs paraméterek becslése, de legtöbbször szinte lehetetlen a populációs paraméterek kiszámítása. Ehelyett véletlenszerű mintákat veszünk a sokaságból, és kiszámítjuk a minta statisztikáit, amelyek várhatóan közelítik a populációs paramétereket. De honnan tudhatjuk, hogy a minták valódi reprezentánsai-e a sokaságnak, vagy hogy ezek a mintastatisztikák mennyire térnek el a populációs paraméterektől? Itt jönnek képbe a konfidenciaintervallumok. Szóval mik ezek az intervallumok? A konfidenciaintervallum a mintastatisztika feletti és alatti értéktartomány, vagy definiálhatjuk úgy is, mint annak valószínűségét, hogy a mintastatisztika körüli értéktartomány tartalmazza a valódi populációs paramétert.

Konfidencia intervallumok Z-statisztikával

Mielőtt elmélyülnénk a témában, ismerkedjünk meg néhány statisztikai terminológiával.

népesség: Az összes hasonló egyed halmaza. Például egy város lakossága, egy főiskola hallgatói stb.

minta: Hasonló egyedek kis halmaza a populációból. Hasonlóképpen a véletlenszerű minta a sokaságból véletlenszerűen vett minta.

paraméterek: Átlag(mu), szórás(szigma), arány(p) a sokaságból származtatva.

statisztikai: átlag (x bar), std eltérés (S), arányok (p^) a mintákra vonatkoztatva.

Z-pontszám: bármely nyers adatpont távolsága a normál eloszláson az átlagostól, normál eltéréssel normalizálva. Által adott: x-mu/sigma

Most már készen állunk, hogy mélyre merüljünk a konfidenciaintervallumok fogalmában. Valamilyen oknál fogva úgy gondolom, hogy sokkal jobb megérteni a fogalmakat összehasonlítható példákon keresztül, nem pedig nyers matematikai meghatározásokon keresztül. Tehát kezdjük.

Tegyük fel, hogy egy 100,000 100 lakosú városban élsz, és választások vannak a sarkon. Közvélemény-kutatóként előre kell jeleznie, hogy ki nyeri a választást, akár a kék, akár a sárga párt. Tehát látja, hogy szinte lehetetlen információt gyűjteni a teljes lakosságról, így véletlenszerűen kiválaszt 62 embert. A felmérés végén azt találta, hogy az emberek 62%-a a sárgára fog szavazni. A kérdés az, hogy levonhatjuk-e azt a következtetést, hogy a sárga nyer 62%-os valószínűséggel, vagy a teljes lakosság 58%-a a sárgára fog szavazni? Nos, a válasz NEM. Nem tudjuk biztosan, milyen messze van a becslésünk a valódi paramétertől, ha újabb mintát veszünk, az eredmény 65% vagy XNUMX% ​​lehet. Tehát ehelyett azt fogjuk tenni, hogy a mintastatisztikáink körül olyan értékeket keresünk, amelyek nagy valószínűséggel megragadják a népesség valódi arányát. Itt az arány a százalékra vonatkozik

                                                                   a kép a szerzőé

Ha most száz ilyen mintát veszünk, és minden minta mintaarányát ábrázoljuk, akkor a mintavételi arányok normális eloszlását kapjuk, és az eloszlás átlaga a populációs arány legközelítőbb értéke lesz. És a becslésünk az eloszlási görbe bármely pontján elhelyezkedhet. A 3 szigma szabály szerint tudjuk, hogy a valószínűségi változók körülbelül 95%-a az eloszlás átlagától 2 std eltérésen belül van. Tehát arra a következtetésre juthatunk, hogy annak a valószínűsége p^ 2 std eltérésen belül van a p az 95%. Vagy azt is kijelenthetjük, hogy annak a valószínűsége, hogy p 2 std eltérésen belül van p^ alatt és felett, szintén 95%. Ez a két állítás gyakorlatilag egyenértékű. Ez a p^ alatti és feletti két pont a konfidenciaintervallumunk.

                                                           a kép a szerzőé

Ha valahogy megtaláljuk a szigmát, ki tudjuk számítani a szükséges intervallumot. De itt a szigma a populációs paraméter, és tudjuk, hogy gyakran szinte lehetetlen kiszámítani, ezért ehelyett mintastatisztikát, azaz standard hibát használunk. Ezt úgy adják meg

ahol p^ = mintaarány, n = minták száma

SE =√(0.62 . 0.38/100) = 0.05

tehát 2xSE = 0.1

Adataink konfidencia intervalluma (0.62-0.1,0.62+0.1) vagy (0.52,0.72). Ahogy a 2xSE-t vettük, ez 95%-os konfidencia intervallumot jelent.

A kérdés az, hogy mi van, ha 92%-os konfidencia intervallumot akarunk létrehozni? Az előző példában megszoroztuk a 2-t SE-vel, hogy 95%-os konfidencia intervallumot hozzunk létre, ez a 2 a 95%-os konfidenciaintervallum z-pontszáma (a pontos érték 1.96), és ez az érték egy z-táblázatból található. A z kritikus értéke 92%-os konfidenciaintervallumhoz 1.75. Hivatkozni ezt cikk a z-pontszám és a z-tábla jobb megértéséhez.

Az intervallum a következőképpen adódik: (p^ + z*.SE , p^-z*.SE).

Ha a mintaarány helyett a minta átlagát adjuk meg, a standard hiba a következő lesz sigma/sqrt(n). Itt a szigma a sokaság std eltérése, mivel gyakran nem rendelkezünk, helyette a minta std eltérését használjuk. De gyakran megfigyelhető, hogy ez a fajta becslés, ahol az átlagot adják meg az eredmény, általában kissé torz. Tehát az ilyen esetekben előnyösebb a t-statisztika használata a z-statisztika helyett.

A z-statisztikával rendelkező konfidenciaintervallum általános képletét a következőképpen adja meg

Itt a statisztika a minta átlagára vagy a minta arányára vonatkozik. szigma_s a sokaság szórása.

A bizalmi intervallumok értelmezése

Nagyon fontos a konfidenciaintervallumok helyes értelmezése. Tekintsük az előző közvélemény-kutatói példát, ahol a 95%-os konfidencia intervallumot (0.52,0.62, 95) számoltuk. Az mit jelent? Nos, a 95%-os konfidenciaintervallum azt jelenti, hogy ha n mintát veszünk a sokaságból, akkor az esetek 95%-ában a származtatott intervallum tartalmazza a valódi populációs arányt. Ne feledje, hogy a 95%-os konfidencia-intervallum nem jelenti azt, hogy 90%-os a valószínűsége annak, hogy az intervallum tartalmazza a valódi populációs arányt. Például 10%-os konfidenciaintervallum esetén, ha 9 mintát veszünk egy sokaságból, akkor az említett intervallum 10-ből XNUMX-szerese tartalmazni fogja a valódi populációs paramétert. A jobb megértés érdekében nézze meg az alábbi képet.

                                                            a kép a szerzőé

Konfidenciaintervallumokra vonatkozó feltételezések a Z-statisztika használatával

Vannak bizonyos feltételezések, amelyeket meg kell vizsgálnunk, hogy érvényes konfidenciaintervallumot hozzunk létre a z-statisztika segítségével.

1. Véletlenszerű minta: A mintáknak véletlenszerűnek kell lenniük. Különböző mintavételi módszerek léteznek, mint például rétegzett mintavétel, egyszerű véletlenszerű mintavétel, klasztermintavétel a véletlenszerű minták készítéséhez.
2. Normál feltétel: Az adatoknak meg kell felelniük ennek a feltételnek np^>=10 és n.(1-p^)>=10. Ez lényegében azt jelenti, hogy a mintaelemek mintavételi eloszlásának normálisnak kell lennie, nem ferde egyik oldalon sem.
3. Független: A mintáknak függetleneknek kell lenniük. A minták számának a teljes sokaság 10%-ánál vagy azzal egyenlőnek kell lennie, vagy ha a mintavétel cserével történik.

Konfidencia intervallumok T-statisztikával

Mi van, ha a minta mérete viszonylag kicsi, és a sokaság szórása nincs megadva, vagy nem feltételezhető? Hogyan készítsünk konfidenciaintervallumot? Nos, itt jön be a t-statisztika. A konfidenciaintervallum meghatározásának alapképlete itt ugyanaz marad, csak z* helyett t*. Az általános képletet a

ahol S = a minta szórása, n = a minták száma

Tegyük fel, hogy Ön egy partit rendezett, és meg akarja becsülni vendégei átlagos sörfogyasztását. Így 20 személyből álló véletlenszerű mintát kapunk, és megmérjük a sörfogyasztást. A mintaadatok szimmetrikusak, átlagos 0f 1200 ml és standard eltérés 120 ml. Tehát most egy 95%-os konfidencia intervallumot szeretne felépíteni.

Tehát megvan a minta std eltérése, a minták száma és a minta átlaga. Csak t*-ra van szükségünk. Tehát a t* egy 95%-os konfidencia-intervallumhoz 19 (n-1 = 20-1) szabadságfokkal 2.093. Tehát a szükséges intervallum a számítás után van (1256.16, 1143.83), 56.16-os hibahatárral. Hivatkozni ezt videó, hogy megtudja, hogyan kell olvasni a t-táblázatot.

Feltételezések a CI-re T-statisztikát használva

Hasonlóan a z-statisztika esetéhez, a t-statisztika esetében is van néhány feltétel, amire figyelnünk kell az adott adatoknál.

1. A mintának véletlenszerűnek kell lennie
2. A mintának normálnak kell lennie. Ahhoz, hogy normális legyen, a minta méretének 30-nál nagyobbnak vagy egyenlőnek kell lennie, vagy ha a szülő adatkészlet, azaz a sokaság nagyjából normális. Vagy ha a minta mérete 30 alatt van, akkor az eloszlásnak nagyjából szimmetrikusnak kell lennie.
3. Az egyéni megfigyeléseknek függetleneknek kell lenniük. Ez azt jelenti, hogy a 10%-os szabályt követi, vagy a mintavétel cserével történik.

T-intervallum készítése párosított adatokhoz

Eddig csak egymintás adatokat használtunk. Most meglátjuk, hogyan szerkeszthetünk t-intervallumot a párosított adatokhoz. A páros adatokban ugyanazon az egyeden két megfigyelést végzünk. Például a tanulók teszt előtti és utáni jegyeinek összehasonlítása, vagy egy gyógyszer és a placebo egy csoportra gyakorolt ​​hatására vonatkozó adatok összehasonlítása. Páros adatokban a 3. oszlopban találtuk a két megfigyelés közötti különbséget. Szokás szerint végigmegyünk egy példán, hogy megértsük ezt a fogalmat is,

K. Egy tanár megpróbálta értékelni egy új tanterv hatását a teszteredményre. Az alábbiakban közöljük a megfigyelések eredményeit.

                                                      a kép a szerzőé

Mivel az átlagkülönbség intervallumait szeretnénk keresni, csak a különbségekre van szükségünk a statisztikákra. Ugyanazt a képletet fogjuk használni, mint korábban

statisztika +- (kritikus érték vagy t-érték) (a statisztika szórása)

x_d = a különbség átlaga, S_d = minta std eltérése, 95%-os CI-re szabadságfok mellett 5 t* a 2.57. A hibahatár = 0.97 és a konfidencia intervallum (4.18,6.13, XNUMX).

Értelmezés: A fenti becslések alapján, amint látjuk, a konfidenciaintervallum nem tartalmaz nulla vagy negatív értékeket. Megállapíthatjuk tehát, hogy az új tanterv pozitív hatással volt a tanulók teszteredményeire. Ha csak negatív értékei voltak, akkor azt mondhatnánk, hogy a tananyagnak negatív hatása volt. Vagy ha nullát tartalmazott, akkor előfordulhat, hogy a különbség nulla volt, vagy a tantervnek nincs hatása a teszteredményekre.

Z-érték vs T-érték

Az elején sok a zűrzavar, hogy mikor mit kell használni. A hüvelykujjszabály az, ha a minta mérete >= 30, és a sokaság szórása z-statisztikát használ. Ha a minta mérete < 30, használjon t-statisztikát. A való életben nincsenek populációs paramétereink, ezért a minta mérete alapján z-t vagy t-t fogunk használni.

Kisebb mintáknál (n<30) a központi Limit Theorem nem érvényesül, hanem egy másik eloszlást, a Student-féle t-eloszlást használjuk. A t-eloszlás hasonló a normál eloszláshoz, de a minta méretétől függően eltérő alakot ölt. A z értékek helyett a kisebb mintáknál nagyobb t értékeket használjuk, ami nagyobb hibahatárt eredményez. Kis mintaméret esetén kevésbé lesz pontos.

Bizalmi intervallumok Pythonnal

A Python hatalmas könyvtárral rendelkezik, amely mindenféle statisztikai számítást támogat, ami egy kicsit megkönnyíti az életünket. Ebben a részben a kisgyermekek alvási szokásaira vonatkozó adatokat tekintjük át. A megfigyelések 20 résztvevője egészséges, normális viselkedésű volt, alvászavaruk nem volt. Célunk a szunyókáló és nem szunyókáló kisgyermekek lefekvés idejének elemzése.

Hivatkozás: Akacem LD, Simpkin CT, Carskadon MA, Wright KP Jr, Jenni OG, Achermann P, et al. (2015) A cirkadián óra időzítése és az alvás különbsége a szunyókáló és a nem szunyókáló kisgyermekek között. PLoS ONE 10(4): e0125181. https://doi.org/10.1371/journal.pone.0125181

Olyan könyvtárakat fogunk importálni, amelyekre szükségünk lesz

import numpy as np import panda as pd from scipy.stats import t pd.set_option('display.max_columns', 30) # set, így láthatja a DataFrame import matematika összes oszlopát

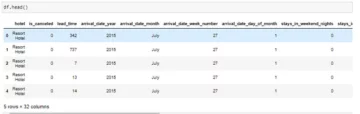
df = pd.read_csv(nap_no_nap.csv) #adatok olvasása

df.head()

Hozzon létre két 95%-os konfidencia intervallumot az átlagos lefekvés idejére, egyet a szunyókáló kisgyermekek számára, egyet pedig a nem alvó kisgyermekek számára. Először is elkülönítjük az „éjszakai lefekvés” oszlopot azok számára, akik egy új változóba szunyókálnak, és azok számára, akik nem szunyókálnak, egy másik új változóba. Az itt lefekvés ideje tizedes.

bedtime_nap = df['éjszakai lefekvés'].loc[df['napping'] == 1] bedtime_no_nap = df['éjszakai lefekvés'].loc[df['napping'] == 0]

print(len(alvásidő_nap))

print(len(lefekvés_no_nap))

kimenet: 15 n 5

Most megtaláljuk a nap és a no_nap átlagos lefekvés idejét.

nap_mean_bedtime = lefekvés_nap.mean() #20.304 no_nap_mean_bedtime = lefekvés_no_nap.mean() #19.59

Most megtaláljuk az X minta szórását_szieszta és X_{nincs szunyókálás} 

nap_s_bedtime = np.std(bedtime_nap,ddof=1) no_nap_s_bedtime = np.std(bedtime_no_nap,ddof=1)

Megjegyzés: A ddof paraméter 1-re van állítva a minta std dev esetében, különben populáció std dev lesz.

Most megtaláljuk az X szabványos hibájának mintáját_szieszta és X_{nincs szunyókálás} 

nap_se_mean_bedtime = nap_s_bedtime/math.sqrt(len(bedtime_nap)) #0.1526 no_nap_se_mean_bedtime = no_nap_s_bedtime/math.sqrt(len(bedtime_no_nap)) #0.2270

Eddig jó, de mivel kicsi a minta mérete és nincs szórása a sokaságaránynak, a t* értéket fogjuk használni. A t* érték megtalálásának egyik módja a használata scipy.stats t.ppf funkció. A t.ppf() argumentumai: q = százalék, df = szabadsági fok, skála = std dev, loc = átlag. Mivel a t-eloszlás szimmetrikus 95%-os konfidenciaintervallumra, q 0.975 lesz. Hivatkozni ezt további információkért a t.ppf().

nap_t_star = t.ppf(0.975,df=14) #2.14 no_nap_t_star = t.ppf(0.975,df=5) #2.57

Most hozzáadjuk a darabokat, hogy végül megalkotjuk a konfidenciaintervallumunkat.

nap_ci_plus = nap_közepes_alvásidő + nap_t_star*nap_se_bedtime

nap_ci_minus = nap_mean_bedtime – nap_t_star*nap_se_bedtime

print(nap_ci_minus,nap_ci_plus)

no_nap_ci_plus = no_nap_mean_bedtime + no_nap_t_star*nap_se_bedtime

no_nap_ci_minus = no_nap_mean_bedtime – no_nap_t_star*nap_se_bedtime

print(no_nap_ci_minus,no_nap_ci_plus)

kimenet: 19.976680775477412 20.631319224522585 18.95974084563192 20.220259154368087

Értelmezés: 

A fenti eredményekből arra a következtetésre jutottunk, hogy 95%-ban biztosak vagyunk abban, hogy a szunyókáló kisgyermekek átlagos lefekvés ideje 19.98 és 20.63 között van, míg a nem szunyókáló kisgyermekeké 18.96 és 20.22 között van. Ezek az eredmények megfelelnek az elvárásunknak, hogy ha napközben szundikál, akkor késő este aludni fog.

EndNotes

Tehát itt az egyszerű konfidenciaintervallumokról volt szó, z és t értékeket használva. Valóban fontos fogalom, amelyet minden statisztikai tanulmány esetében ismerni kell. Remek következtető statisztikai módszer a populációs paraméterek mintaadatokból történő becslésére. A konfidenciaintervallumok a hipotézisvizsgálathoz is kapcsolódnak, miszerint 95%-os CI esetén 5% teret hagy az anomáliáknak. Ha a nullhipotézis a konfidencia intervallumon belülre esik, akkor a p-érték nagy lesz, és nem tudjuk elutasítani a nullát. Ellenkező esetben, ha túlmegy, akkor elegendő bizonyítékunk lesz a nulla elvetésére és az alternatív hipotézisek elfogadására.

Remélem tetszett a cikk és boldog új évet (:

A cikkben bemutatott média nem az Analytics Vidhya tulajdona, és a Szerző belátása szerint használja azokat.

Összefüggő

Forrás: https://www.analyticsvidhya.com/blog/2022/01/understanding- luottamus-intervals-with-python/