Teori Medan Kuantum Membuka Teka-teki Matematika

Bulan lalu, Karen Vogtmann dan Michael Borinsky memposting bukti bahwa ada muatan truk struktur matematika dalam dunia matematika yang sampai sekarang tidak dapat diakses yang disebut ruang moduli grafik, yang Vogtmann dan seorang kolaborator pertama kali dijelaskan di pertengahan 1980.

“Itu masalah yang sangat sulit. Sungguh menakjubkan mereka bisa melakukannya, ”kata Dan Margalit, ahli matematika di Georgia Institute of Technology.

Vogtmann dan Borinsky memulai dengan pertanyaan yang telah ditanyakan Vogtmann, seorang ahli matematika di University of Warwick, selama beberapa dekade. Pasangan ini kemudian menata kembali masalah tersebut dalam bahasa fisika, menggunakan teknik dari teori medan kuantum untuk menghasilkan hasilnya.

Buktinya menunjukkan bahwa struktur tertentu ada di ruang moduli, tetapi tidak secara eksplisit mengungkapkan struktur apa itu. Dengan cara itu, hasil baru mereka lebih mirip detektor logam daripada kamera — ini memberi tahu mereka bahwa ada sesuatu yang menarik yang disembunyikan, meskipun mereka tidak dapat mendeskripsikannya sepenuhnya.

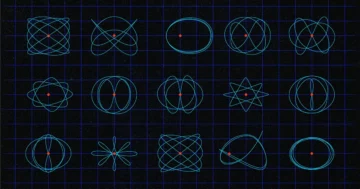
Anda dapat menganggap ruang moduli grafik sebagai bentuk matematis dengan dekorasi tambahan. Jika Anda berdiri di sembarang titik pada bentuk, Anda akan melihat grafik mengambang di atas Anda — kumpulan titik, atau simpul, yang dihubungkan oleh tepi. Di lokasi berbeda pada ruang moduli, grafik berubah, tepinya menyusut atau membesar, dan terkadang menghilang sama sekali. Karena fitur-fitur ini, Borinsky, fisikawan matematika di Swiss Federal Institute of Technology Zurich, menggambarkan ruang moduli sebagai “lautan grafik yang besar”.

"Peringkat" grafik adalah jumlah loop yang dimilikinya; untuk setiap peringkat grafik, terdapat ruang moduli. Ukuran ruang ini tumbuh dengan cepat — jika Anda memperbaiki panjang tepi grafik, ada tiga grafik peringkat 2, 15 peringkat 3, 111 peringkat 4, dan 2,314,204,852 peringkat 10. Pada ruang moduli, panjang ini bisa bervariasi, memperkenalkan lebih banyak kompleksitas.

Bentuk ruang moduli untuk grafik dari peringkat tertentu ditentukan oleh hubungan antar grafik. Saat Anda berjalan di sekitar ruang, grafik terdekat harus serupa, dan harus berubah dengan lancar menjadi satu sama lain. Tetapi hubungan ini rumit, meninggalkan ruang moduli dengan ciri-ciri yang meresahkan secara matematis, seperti daerah di mana tiga dinding ruang moduli saling berpapasan.

Ahli matematika dapat mempelajari struktur suatu ruang atau bentuk menggunakan objek yang disebut kelas kohomologi, yang dapat membantu mengungkapkan bagaimana suatu ruang disatukan. Misalnya, pertimbangkan salah satu bentuk favorit matematikawan, donat. Di donat, kelas kohomologi hanyalah loop.

Seseorang dapat menggambar beberapa jenis lingkaran yang berbeda pada permukaan donat: Lingkaran 1 melingkari lubang tengah donat; lingkarkan 2 benang melalui lubang; loop "sepele" ketiga berada di sisi donat.

Namun, tidak semua kelas kohomologi diciptakan sama. Lingkaran yang terletak di bagian luar donat — seperti lingkaran ketiga — selalu dapat bergeser atau menyusut untuk menghindari perpotongan lingkaran lainnya. Itu membuatnya menjadi kelas kohomologi "sepele".

Tetapi loop 1 dan 2 mengatakan lebih banyak tentang struktur donat - mereka hanya ada karena lubangnya. Untuk mengetahui perbedaan secara matematis, Anda dapat menggunakan persimpangan, jelas Margalit. Loop 1 dan 2 dapat meluncur di sekitar permukaan donat, tetapi kecuali Anda memaksanya untuk melepaskan diri dari permukaan sama sekali, mereka akan selalu bersinggungan. Karena kedua loop ini datang dengan pasangan yang tidak bisa tidak mereka silangkan, mereka adalah kelas kohomologi “nontrivial”.

Berbeda dengan donat, ahli matematika tidak dapat menemukan kelas kohomologi pada ruang moduli grafik hanya dengan menggambar gambar. Dengan jumlah grafik yang begitu besar, ruang moduli sulit untuk dipahami, kata Nathalie Wahl, ahli matematika di Universitas Kopenhagen. “Sangat cepat, komputer tidak bisa membantu lagi,” katanya. Memang, hanya satu kelas kohomologi nontrivial dimensi ganjil yang pernah ada dihitung secara eksplisit (dalam 11 dimensi), bersama dengan segelintir yang genap.

Apa yang Vogtmann dan Borinsky buktikan adalah bahwa ada sejumlah besar kelas kohomologi yang terletak di dalam ruang moduli grafik dari peringkat tertentu — meskipun kita tidak dapat menemukannya. "Kami tahu ada banyak sekali, dan kami tahu satu," kata Wahl, menyebut keadaan itu "konyol".

Alih-alih bekerja dengan kelas kohomologi secara langsung, Borinsky dan Vogtmann mempelajari nomor yang disebut karakteristik Euler. Angka ini memberikan jenis pengukuran ruang moduli. Anda dapat memodifikasi ruang moduli dengan cara tertentu tanpa mengubah karakteristik Eulernya, menjadikan karakteristik Euler lebih mudah diakses daripada kelas kohomologi itu sendiri. Dan itulah yang dilakukan Borinsky dan Vogtmann. Alih-alih bekerja dengan ruang moduli grafik secara langsung, mereka mempelajari "tulang belakang" - pada dasarnya kerangka dari keseluruhan ruang. Tulang belakang memiliki karakteristik Euler yang sama dengan ruang moduli itu sendiri dan lebih mudah untuk dikerjakan. Menghitung karakteristik Euler pada tulang belakang bermuara pada menghitung kumpulan besar pasangan grafik.

Wawasan Borinsky adalah menggunakan teknik untuk menghitung diagram Feynman, yaitu grafik yang menunjukkan cara partikel kuantum berinteraksi. Ketika fisikawan ingin menghitung, katakanlah, kemungkinan tumbukan antara elektron dan positron akan menghasilkan dua foton, mereka perlu menjumlahkan semua kemungkinan interaksi yang mengarah pada hasil tersebut. Itu berarti rata-rata pada banyak diagram Feynman, memotivasi strategi penghitungan yang cerdas.

"Saya menyadari bahwa seseorang dapat merumuskan masalah semacam ini sebagai semacam mainan alam semesta teori medan kuantum," jelas Borinsky.

Borinsky membayangkan grafik tersebut mewakili sistem fisik dalam versi sederhana alam semesta, di mana, di antara asumsi lainnya, hanya ada satu jenis partikel. Kerangka teori medan kuantum membutuhkan beberapa penyesuaian untuk Borinsky dan Vogtmann untuk mendapatkan hitungan yang tepat. Misalnya, dalam teori medan kuantum, dua grafik yang merupakan bayangan cermin satu sama lain tidak dapat dibedakan, kata Borinsky. Rumus untuk menjumlahkan diagram Feynman mencakup faktor-faktor yang memastikan grafik ini tidak dihitung secara berlebihan. Namun ketika menghitung karakteristik Euler, grafik tersebut dianggap berbeda. “Kita harus memainkan permainan kecil dengan simetri grafik,” kata Borinsky.

Dengan beberapa bantuan pemrograman dari fisikawan Jos Vermaseren, Borinsky dan Vogtmann akhirnya mengatasi kesulitan ini. Dalam makalah Januari mereka, mereka membuktikan bahwa karakteristik Euler dari ruang moduli grafik peringkat n mendapat besar-besaran negatif sebagai n semakin besar. Ini menyiratkan bahwa ada banyak, banyak kelas kohomologi nontrivial yang akan diungkap dalam setiap ruang moduli.

Meskipun makalah Borinsky dan Vogtmann tidak berisi petunjuk lebih lanjut tentang kelas kohomologi ini, ini merupakan hasil yang menggembirakan bagi para peneliti yang berusaha menemukannya - dan mungkin menambah sensasi perburuan. Kata Margalit dari kelas kohomologi: “Yang kami tahu hanyalah permata ini. Dan setiap kali kami menemukannya, itu adalah hal yang indah ini.