Introduzione
I minimi quadrati ordinari sono una tecnica di ottimizzazione. OLS è la stessa tecnica utilizzata dalla classe scikit-learn LinearRegression e dalla funzione numpy.polyfit() dietro le quinte. Prima di procedere nei dettagli della tecnica OLS, varrebbe la pena leggere l'articolo su cui ho scritto il ruolo delle tecniche di ottimizzazione nel machine learning e nel deep learning. Nello stesso articolo, ho spiegato brevemente il motivo e il contesto dell'esistenza della tecnica OLS (sezione 6). Questo articolo è in gran parte la continuazione dello stesso articolo e ci si aspetta che i lettori abbiano familiarità con lo stesso.

Fonte: Pixbay
Obiettivi formativi:
In questo articolo, lo farai
- Scopri cos'è OLS e comprendi la sua equazione matematica
- Ottieni una panoramica di OLS in forma di scaler e dei suoi svantaggi
- Comprendere OLS utilizzando un esempio in tempo reale
Sommario
- Cosa sono i problemi di ottimizzazione?
- Perché abbiamo bisogno di OLS?
- Comprensione della matematica dietro l'algoritmo OLS
- Soluzione OLS in forma Scaler
- OLS in azione utilizzando un esempio reale
- Problemi con la forma Scaler della soluzione OLS
- Conclusione
Cosa sono i problemi di ottimizzazione?
I problemi di ottimizzazione sono problemi matematici che implicano la ricerca della soluzione migliore da un insieme di possibili soluzioni. Questi problemi sono tipicamente formulati come problemi di massimizzazione o minimizzazione, in cui l'obiettivo è massimizzare o minimizzare una certa funzione obiettivo. La funzione obiettivo è un'espressione matematica che descrive la quantità da ottimizzare e un insieme di vincoli definisce l'insieme delle possibili soluzioni.
I problemi di ottimizzazione sorgono in vari campi, tra cui ingegneria, finanza, economia e ricerca operativa. Sono utilizzati per modellare e risolvere problemi come l'allocazione delle risorse, la pianificazione e l'ottimizzazione del portafoglio. L'ottimizzazione è una componente cruciale di molti algoritmi di machine learning. Nell'apprendimento automatico, l'ottimizzazione viene utilizzata per trovare il miglior set di parametri per un modello che riduca al minimo la differenza tra le previsioni del modello e i valori reali. L'ottimizzazione è un'area di ricerca attiva nell'apprendimento automatico, con nuovi algoritmi di ottimizzazione in fase di sviluppo per migliorare la velocità e l'accuratezza dell'addestramento dei modelli di apprendimento automatico.
Alcuni esempi di dove l'ottimizzazione viene utilizzata nell'apprendimento automatico includono:
- Nell'apprendimento supervisionato, l'ottimizzazione viene utilizzata per trovare i parametri di un modello che riducono al minimo la differenza tra le previsioni del modello e i valori reali per un determinato set di dati di addestramento. Ad esempio, la regressione lineare e la regressione logistica utilizzano l'ottimizzazione per trovare i migliori valori dei coefficienti del modello. Inoltre, alcuni modelli come alberi decisionali, foreste casuali e modelli di aumento del gradiente vengono creati aggiungendo in modo iterativo nuovi modelli all'insieme e ottimizzando i parametri dei nuovi modelli che riducono al minimo l'errore sui dati di addestramento.
- Nell'apprendimento non supervisionato, l'ottimizzazione aiuta a trovare la migliore configurazione dei cluster o la mappatura dei dati che rappresenta al meglio la struttura sottostante nei dati. Nel il clustering, l'ottimizzazione viene utilizzata per trovare la migliore configurazione dei cluster nei dati. Ad esempio, l'algoritmo K-Means utilizza una tecnica di ottimizzazione chiamata algoritmo di Lloyd, che riassegna in modo iterativo i punti dati al centroide del cluster più vicino e aggiorna i centroidi del cluster in base ai nuovi punti assegnati. Allo stesso modo, anche altri algoritmi di clustering come il clustering gerarchico, il clustering basato sulla densità e i modelli di miscela gaussiana utilizzano tecniche di ottimizzazione per trovare la migliore soluzione di clustering. Nel riduzione della dimensionalità, l'ottimizzazione trova la migliore mappatura dei dati da uno spazio di dimensione elevata a uno di dimensione inferiore. Ad esempio, l'analisi delle componenti principali (PCA) utilizza la decomposizione del valore singolare (SVD), una tecnica di ottimizzazione, per trovare la migliore combinazione lineare delle variabili originali che spiega la maggior varianza nei dati. Inoltre, anche altre tecniche di riduzione della dimensionalità come l'analisi discriminante lineare (LDA) e l'incorporamento del vicino stocastico t-distribuito (t-SNE) utilizzano tecniche di ottimizzazione per trovare la migliore rappresentazione dei dati in uno spazio dimensionale inferiore.
- Nell'apprendimento profondo, l'ottimizzazione viene utilizzata per trovare il miglior set di parametri per le reti neurali, che in genere viene eseguita utilizzando algoritmi di ottimizzazione basati sul gradiente come la discesa del gradiente stocastico (SGD) o Adam/Adagrad/RMSProp e così via.
Perché abbiamo bisogno di OLS?
I minimi quadrati ordinari (OLS) è un metodo per stimare i parametri di un modello di regressione lineare. L'algoritmo OLS mira a trovare i valori dei parametri del modello di regressione lineare (cioè i coefficienti) che minimizzano la somma dei quadrati dei residui. I residui sono le differenze tra i valori osservati della variabile dipendente e i valori previsti della variabile dipendente date le variabili indipendenti. È importante notare che l'algoritmo OLS presuppone che gli errori siano distribuiti normalmente con media nulla e varianza costante e che non vi sia multicollinearità (alta correlazione) tra le variabili indipendenti. Altri metodi, come i minimi quadrati generalizzati o i minimi quadrati ponderati, dovrebbero essere utilizzati nei casi in cui queste ipotesi non sono soddisfatte.
Comprensione della matematica dietro l'algoritmo OLS
Per spiegare l'algoritmo OLS, lasciatemi prendere l'esempio più semplice possibile. Considera i seguenti 3 punti dati:
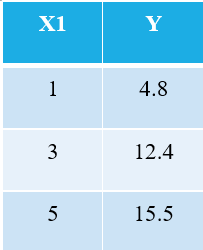
Chiunque abbia familiarità con l'apprendimento automatico riconoscerà immediatamente che ci riferiamo a X1 come variabile indipendente (chiamata anche "Caratteristiche" o "Attributi"), e la Y è la variabile dipendente (nota anche come "Bersaglio" or "Risultato"). Quindi, il compito generale di qualsiasi macchina è trovare la relazione tra X1 e Y. Questa relazione è in realtà "imparato" dalla macchina dal DATI. Quindi, chiamiamo il termine Machine Learning. Noi umani impariamo dalle nostre esperienze. Allo stesso modo, la stessa esperienza viene immessa nella macchina sotto forma di dati.
Ora, supponiamo di voler trovare la linea più adatta attraverso i 3 punti dati sopra. Il grafico seguente mostra questi 3 punti dati in cerchi blu. Viene mostrata anche la linea rossa (con quadrati), che rivendichiamo come "linea più adatta” attraverso questi 3 punti dati. Inoltre, ho mostrato una linea di "scarso adattamento" (la linea gialla) per il confronto.
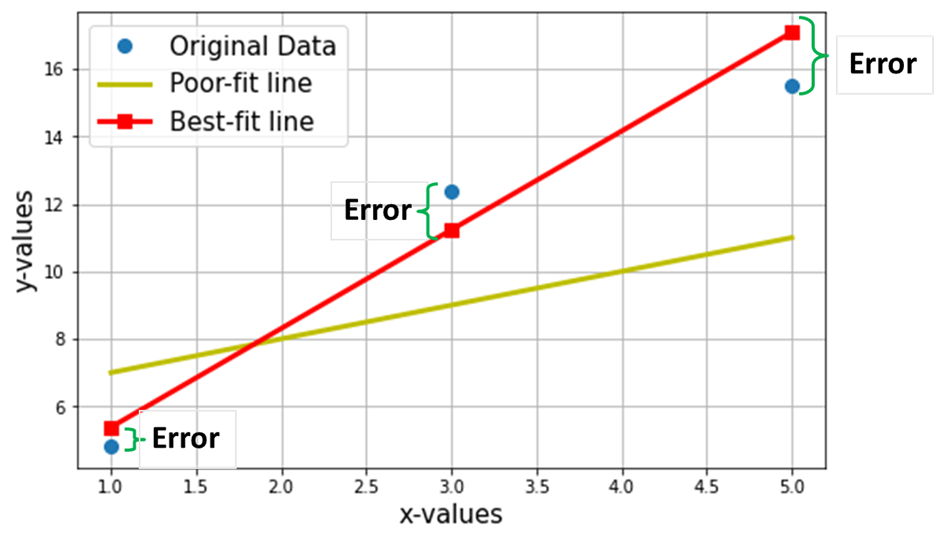
L'obiettivo netto è quello di trovare l'equazione del Linea retta più aderente (attraverso questi 3 punti dati menzionati nella tabella sopra).

È l'equazione della linea più adatta (linea rossa nel grafico sopra), dove w1 = pendenza della retta; w0 = intercettazione della linea.
Nell'apprendimento automatico, questa soluzione migliore è chiamata Lineare Regressione (LR) modello e sono anche chiamati w0 e w1 pesi del modello o coefficienti del modello.
I quadrati rossi nel grafico sopra rappresentano i valori previsti dal modello di regressione lineare (Y^). Naturalmente, i valori previsti NON sono gli stessi dei valori effettivi di Y (cerchi blu). La differenza verticale rappresenta l'errore nella previsione data da (vedi l'immagine sotto) per ogni i-esimo punto dati.
![]()
Ora sostengo che questa migliore linea di adattamento avrà l'errore minimo per la previsione (tra tutte le possibili infinite linee casuali di "scarso adattamento"). Questo errore totale in tutti i punti dati è espresso come il Funzione errore quadratico medio (MSE)., che sarà il file ordine per la linea più adatta.
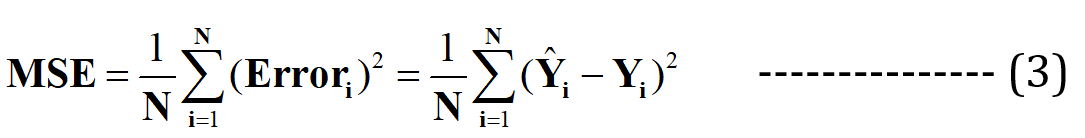
N = Totale n. di punti dati nel set di dati (nel caso corrente, è 3)
La minimizzazione o la massimizzazione di qualsiasi quantità è definita matematicamente come an Problema di ottimizzazione, e quindi la soluzione (il punto in cui esiste il minimo/massimo) si riferisce ai valori ottimali delle variabili.

Regressione lineare è un esempio di ottimizzazione non vincolata, dato da:
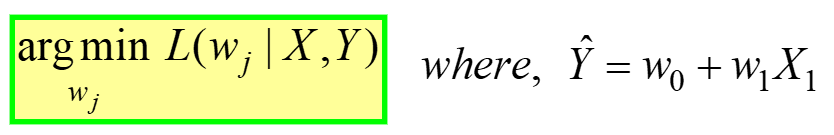 ---- (4)
---- (4)
Questo viene letto come "Trova il pesi ottimali (wj) per cui il MSE La funzione di perdita (data nell'eq. 3 sopra) ha valore minimo, per DATI i dati X, Y" (fare riferimento alla primissima tabella all'inizio dell'articolo). L(lj) rappresenta la perdita MSE, una funzione dei pesi del modello, non X o Y. Ricorda, X e Y sono i tuoi DATI e dovrebbero essere COSTANTI! Il pedice “j” rappresenta il j-esimo coefficiente/peso del modello.
Sostituendo Y^ = w0 +w1X1 nell'eq. 3 sopra, il finale Funzione di perdita MSE (L) sembra:
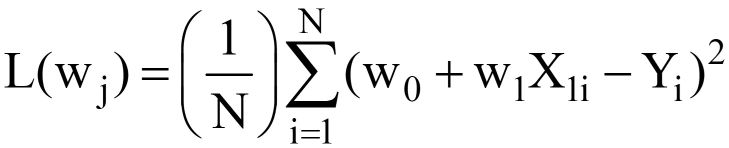 ---- (5)
---- (5)
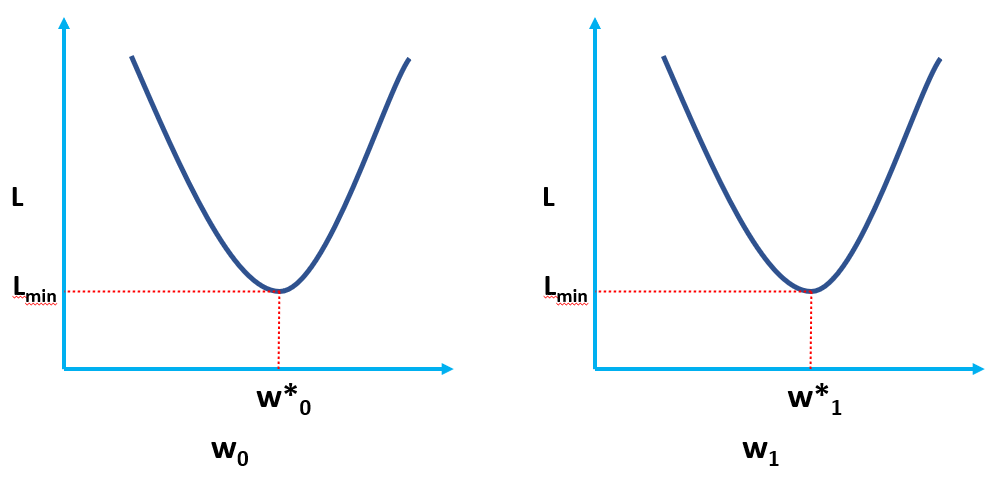
Chiaramente, L è una funzione dei pesi del modello (w0 & w1), di cui dobbiamo trovare i valori ottimali minimizzando L. I valori ottimali sono rappresentati da (*) nella figura sottostante.
Soluzione OLS in forma Scaler
L'eq. 5 sopra riportato rappresenta la funzione OLS Loss nella forma scaler (dove possiamo vedere il sommatoria degli errori per ogni punto dati. L'algoritmo OLS è una soluzione analitica al problema di ottimizzazione presentato nell'eq. 4. Questa soluzione analitica consiste nelle seguenti fasi:
Passo 1:

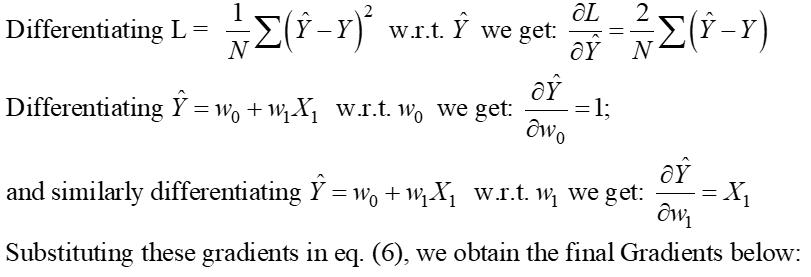

Passaggio 2: equiparare questi gradienti a zero e risolvere i valori ottimali dei coefficienti del modello wj.
Ciò significa sostanzialmente che la pendenza della tangente (l'interpretazione geometrica dei gradienti) alla funzione di perdita ai valori ottimali (il punto in cui L è minimo) sarà zero, come mostrato nelle figure sopra.

Dalle equazioni di cui sopra, possiamo spostare il "2" da sinistra a destra; la destra rimane 0 (poiché 0/2 è ancora 0).


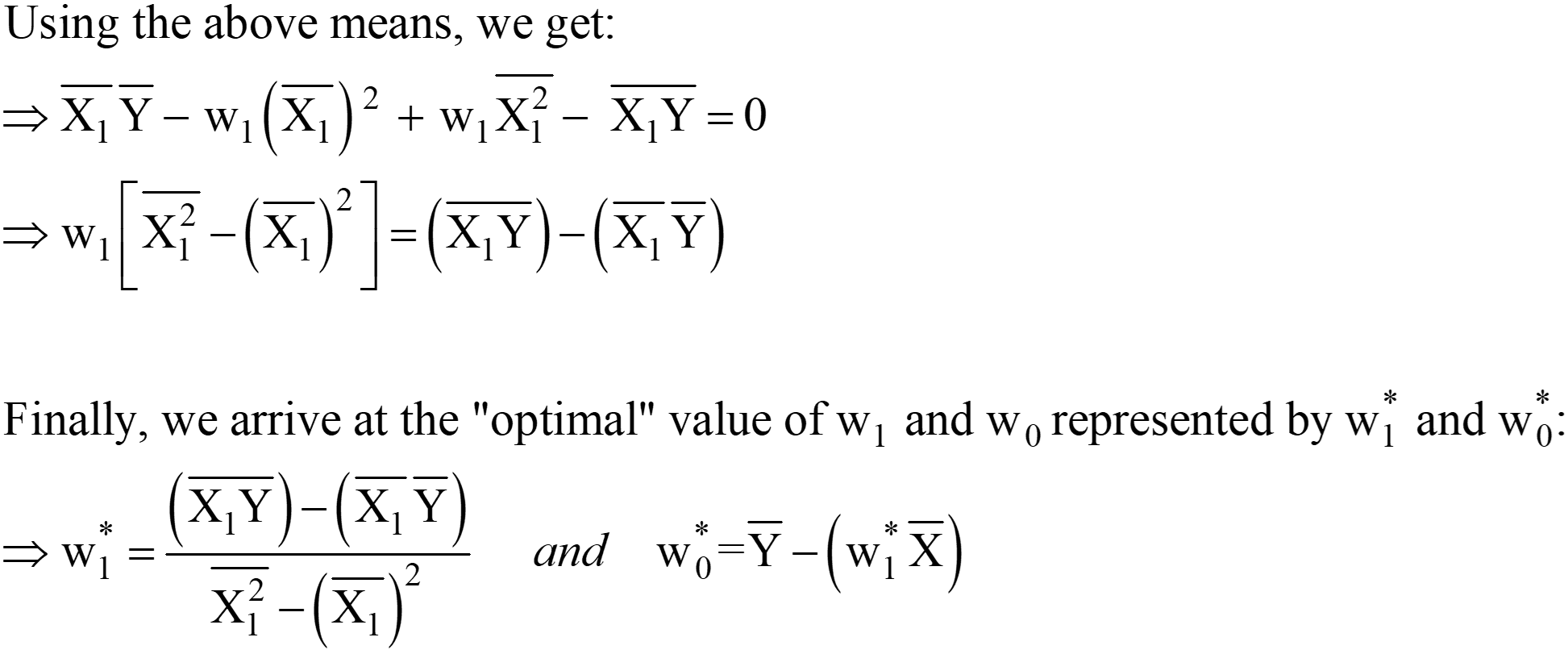
Queste espressioni per w1* e w0* sono la soluzione analitica OLS finale nella forma Scaler.
Passaggio 3: calcola le medie di cui sopra e sostituisci nell'espressione w1* e w0*.
Calcoliamo questi valori per il nostro set di dati:
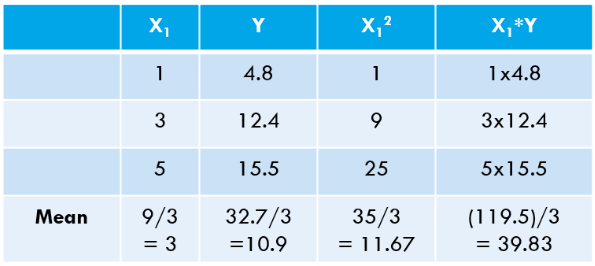
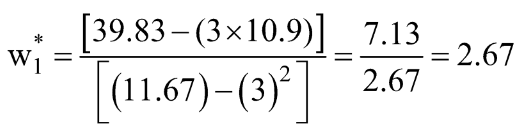
![]()
Calcoliamo lo stesso usando il codice Python:
[OUTPUT]: Questa è l'equazione della linea "Best-fit": 2.675 x + 2.875
Puoi vedere che i nostri valori "calcolati a mano" corrispondono molto da vicino ai valori di pendenza e intercetta ottenuti usando NumPy (la piccola differenza è dovuta a errori di arrotondamento nei nostri calcoli manuali). Possiamo anche verificare che lo stesso OLS è "in esecuzione dietro le quinte" della classe LinearRegression da scikit-impara pacchetto, come dimostrato nel codice seguente.
# importa la classe LinearRegression dal pacchetto scikit-learn da sklearn.linear_model import LinearRegression LR = LinearRegression() # crea un'istanza della classe LinearRegression # definisce X e Y come NumPy Array (vettori colonna) X = np.array([1,3,5 ,1,1]).reshape(-4.8,12.4,15.5) Y = np.array([1,1]).reshape(-0) LR.fit(X,Y) # calcola i coefficienti del modello LR .intercept_ # il bias o il termine di intercettazione (wXNUMX*)
[Uscita]: matrice([2.875])
LR.coef_ # il termine della pendenza (w1*) [Output]: array([[2.675]])
OLS in azione utilizzando un esempio reale
Qui sto usando il set di dati Boston House Pricing, uno dei set di dati più comunemente incontrati durante l'apprendimento di Data Science. L'obiettivo è quello di fare un Modello di regressione lineare Predire il valore mediano dei prezzi delle case in base a 13 caratteristiche/attributi menzionati di seguito.
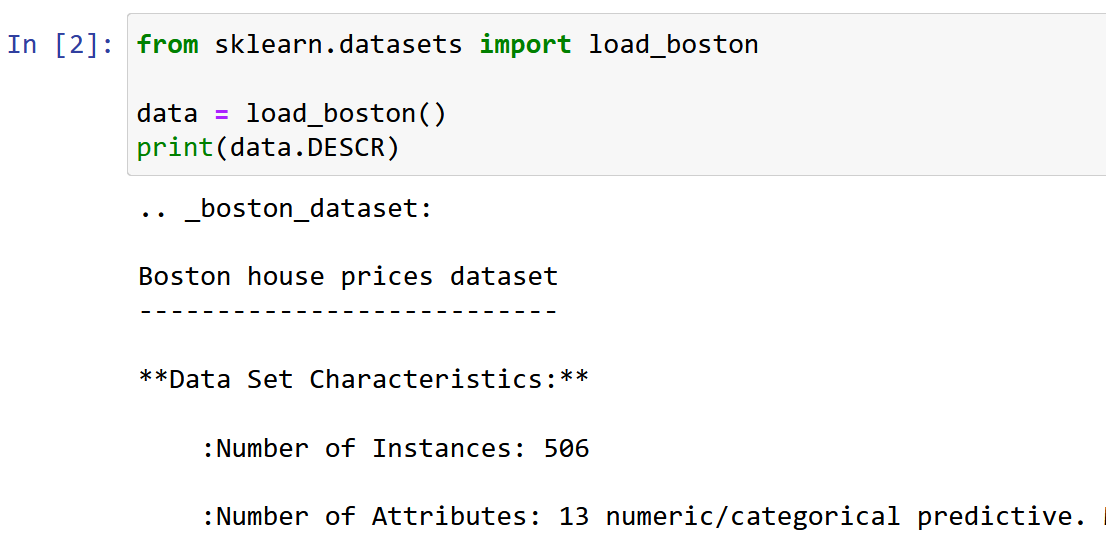
Importa ed esplora il set di dati.
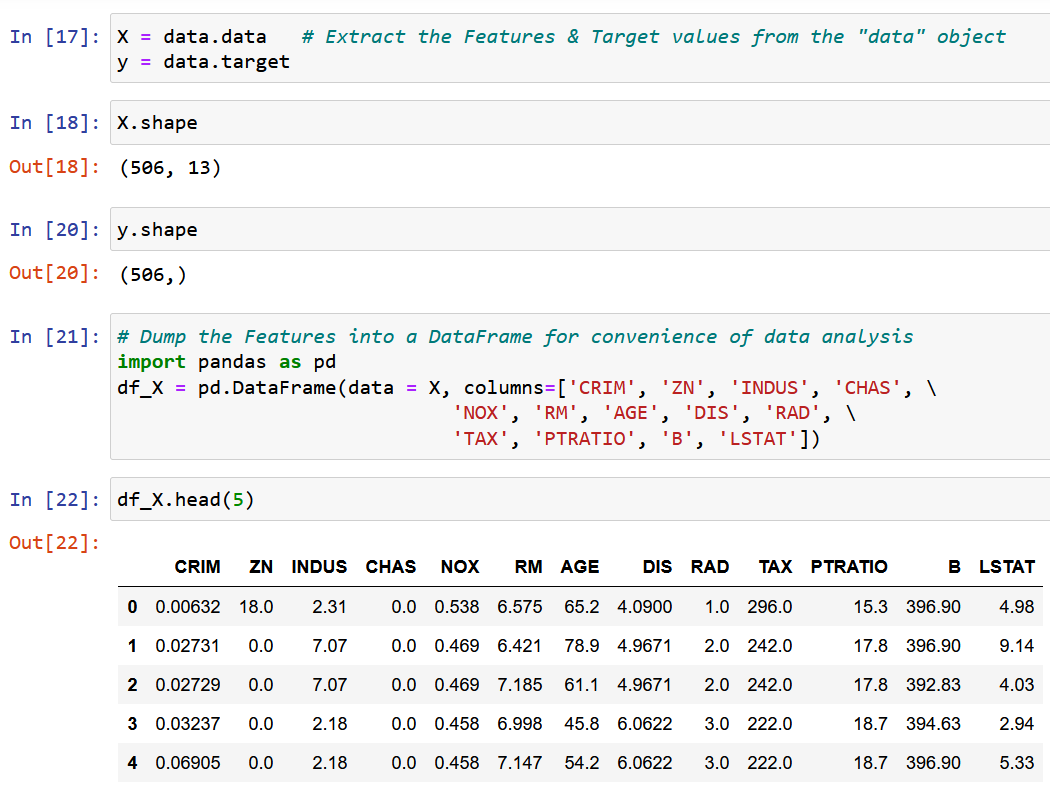
Estraiamo una singola caratteristica RM, la dimensione media della stanza nella località data, e la adattiamo con la variabile target y (il valore mediano del prezzo della casa).
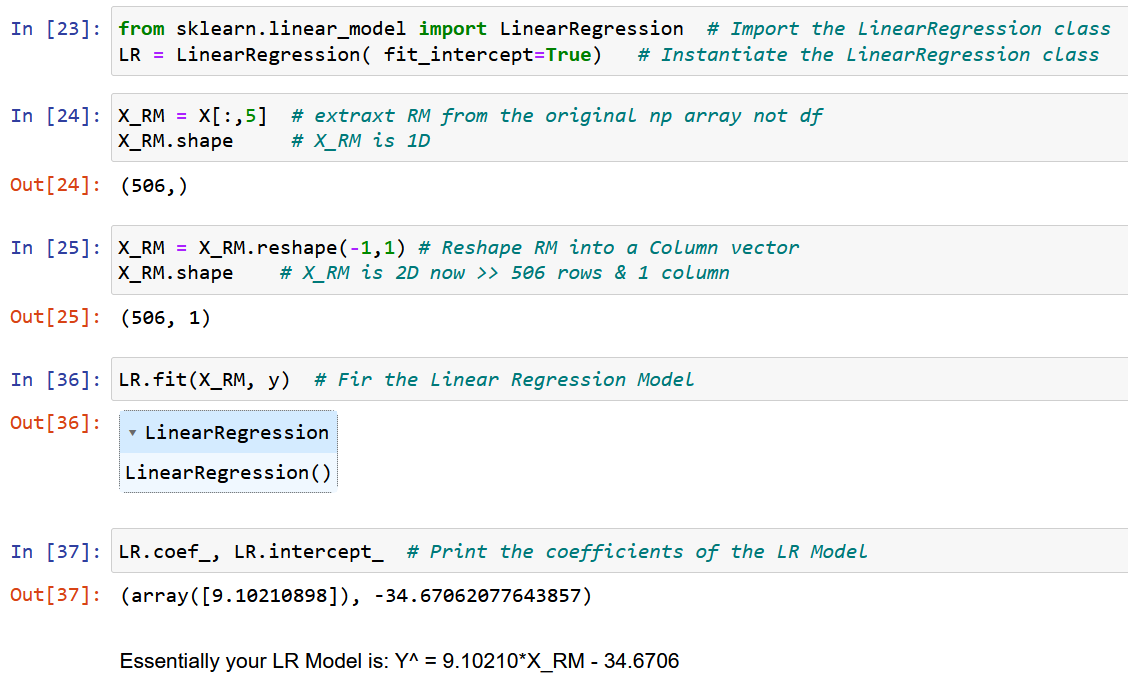
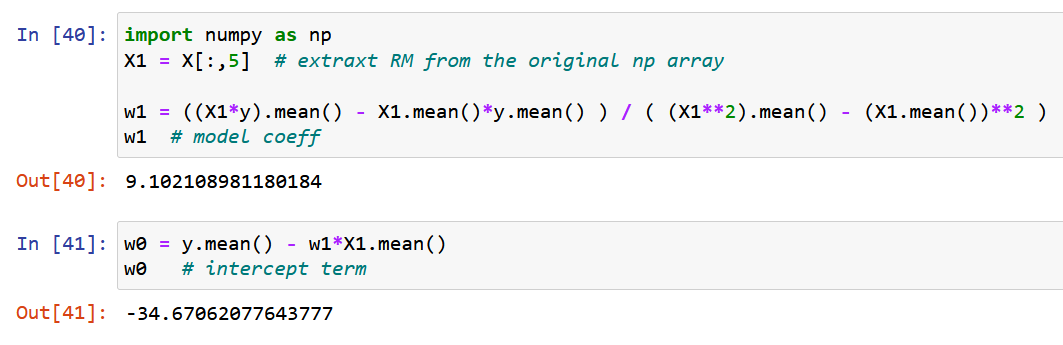
Ora, usiamo NumPy puro e calcoliamo i coefficienti del modello utilizzando le espressioni derivate per i valori ottimali dei coefficienti del modello w0 e w1 sopra (fine del passaggio 2).
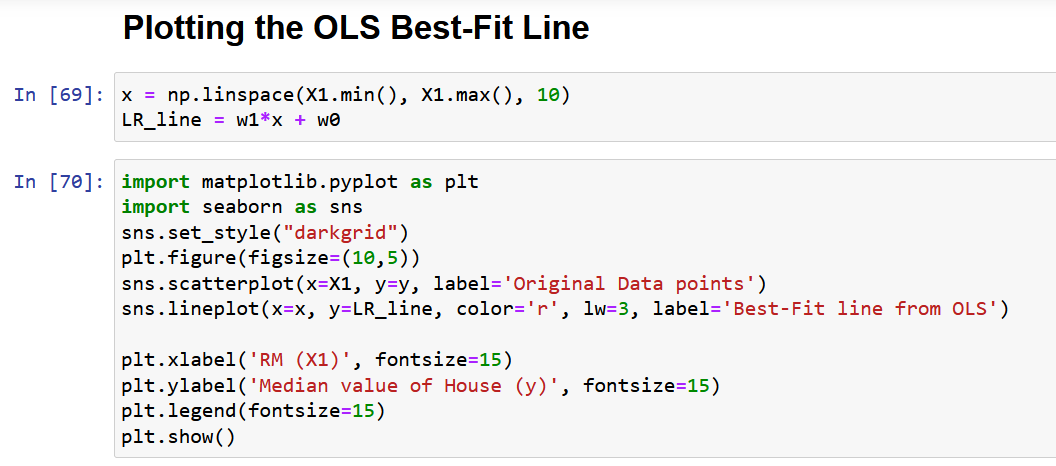
Tracciamo infine i dati originali insieme alla linea di miglior adattamento, come indicato di seguito.

Problemi con la forma Scaler della soluzione OLS
Infine, vorrei discutere il problema principale con l'approccio di cui sopra, come descritto nella sezione 4. Come puoi vedere dal set di dati sopra menzionato, qualsiasi set di dati della vita reale avrà più caratteristiche. Il motivo principale per cui ho preso solo una caratteristica per dimostrare il metodo OLS nella sezione precedente era che all'aumentare del numero di caratteristiche, aumenterebbe anche il numero di gradienti, quindi il numero di equazioni da risolvere simultaneamente!
Per l'esattezza, per 13 caratteristiche (dataset di Boston sopra), avremo 13 coefficienti del modello e un termine di intercettazione, che porta il numero totale di variabili da ottimizzare a 14. Quindi, otterremo 14 gradienti (la derivata parziale della funzione di perdita rispetto a ciascuna di queste 14 variabili). Di conseguenza, dobbiamo risolvere 14 equazioni (dopo aver equiparato queste 14 derivate parziali a zero, come descritto nel passaggio 2). Hai già realizzato la complessità della soluzione analitica con solo 2 variabili. Francamente, ho provato a darti la spiegazione più elaborata di OLS disponibile su Internet, eppure non è facile assimilare la matematica.
Quindi, in parole semplici, la suddetta soluzione analitica NON È SCALABILE!
La soluzione a questo problema è la "Forma vettorizzata della soluzione OLS", che sarà discussa in dettaglio in un articolo di follow-up (Parte 2 di questo articolo), con sezioni 7 e 8.
Conclusione
In conclusione, il metodo OLS è un potente strumento per stimare i parametri di un modello di regressione lineare. Si basa sul principio di minimizzare la somma dei quadrati delle differenze tra i valori previsti e quelli effettivi.
Alcuni dei punti chiave dell'articolo sono i seguenti:
- La soluzione OLS può essere rappresentata in forma scaler, rendendola facile da implementare e interpretare.
- L'articolo ha discusso il concetto di problemi di ottimizzazione e la necessità di OLS nell'analisi di regressione e ha fornito una formulazione matematica e un esempio di OLS in azione.
- L'articolo evidenzia anche alcune delle limitazioni della forma scaler della soluzione OLS, come la scalabilità e le ipotesi di linearità e varianza costante. Spero che tu abbia imparato qualcosa di nuovo da questo articolo.
Per favore lasciami un commento se ritieni che qualche punto/equazione in questo articolo necessiti di una spiegazione o se vuoi che scriva su qualsiasi altro algoritmo di apprendimento automatico in modo così dettagliato.
Leggi Anche
- Distribuzione di contenuti basati su SEO e PR. Ricevi amplificazione oggi.
- Platoblockchain. Web3 Metaverse Intelligence. Conoscenza amplificata. Accedi qui.
- Fonte: https://www.analyticsvidhya.com/blog/2023/01/a-comprehensive-guide-to-ols-regression-part-1/
- 1
- 10
- 214
- 7
- a
- Chi siamo
- sopra
- Assoluta
- precisione
- operanti in
- Action
- attivo
- effettivamente
- aggiunta
- Inoltre
- Dopo shavasana, sedersi in silenzio; saluti;
- mira
- algoritmo
- Algoritmi
- Tutti
- assegnazione
- già
- tra
- .
- Analitico
- ed
- approccio
- RISERVATA
- articolo
- addetto
- disponibile
- media
- basato
- fondamentalmente
- prima
- dietro
- dietro le quinte
- essendo
- sotto
- MIGLIORE
- fra
- pregiudizio
- Blu
- potenziamento
- Boston
- brevemente
- Porta
- costruito
- chiamata
- detto
- Custodie
- casi
- centro
- certo
- cerchi
- rivendicare
- classe
- strettamente
- Cluster
- il clustering
- codice
- Colonna
- combinazione
- commento
- comunemente
- confronto
- complessità
- componente
- globale
- Calcolare
- concetto
- conclusione
- Configurazione
- conseguentemente
- Prendere in considerazione
- costante
- vincoli
- contesto
- continuazione
- Correlazione
- corso
- creare
- cruciale
- Corrente
- Scuro
- dati
- punti dati
- scienza dei dati
- dataset
- decisione
- deep
- definisce
- dimostrato
- dimostrando
- dipendente
- Derivati
- derivato
- descritta
- dettaglio
- dettagli
- sviluppato
- differenza
- differenze
- discutere
- discusso
- distribuito
- Cadere
- ogni
- Economia
- o
- Elaborare
- Ingegneria
- equazioni
- errore
- errori
- eccetera
- Etere (ETH)
- esempio
- Esempi
- esiste
- previsto
- esperienza
- Esperienze
- Spiegare
- ha spiegato
- Spiega
- spiegazione
- esplora
- espresso
- espressioni
- estratto
- familiare
- caratteristica
- Caratteristiche
- Federale
- campi
- figura
- Cifre
- finale
- Infine
- finanziare
- Trovare
- ricerca
- trova
- Nome
- in forma
- i seguenti
- segue
- modulo
- da
- function
- Dare
- dato
- scopo
- andando
- gradienti
- Gruppo
- guida
- aiuta
- Alta
- evidenzia
- speranza
- Casa
- HTTPS
- Gli esseri umani
- Immagine
- subito
- realizzare
- importare
- importante
- competenze
- in
- includere
- Compreso
- Aumento
- studente indipendente
- esempio
- Internet
- interpretazione
- coinvolgere
- IT
- Le
- IMPARARE
- apprendimento
- LG
- limiti
- linea
- Linee
- SEMBRA
- spento
- macchina
- machine learning
- Principale
- make
- Fare
- molti
- mappatura
- partita
- matematico
- matematicamente
- matematica
- max-width
- Massimizzare
- si intende
- menzionato
- metodo
- metodi
- minimizzazione
- minimizzando
- ordine
- miscela
- modello
- modelli
- maggior parte
- multiplo
- Bisogno
- esigenze
- rete
- reti
- Neurale
- reti neurali
- New
- normalmente
- numero
- numpy
- obiettivo
- Obiettivi d'Esame
- ottenuto
- ONE
- Operazioni
- ottimale
- ottimizzazione
- OTTIMIZZA
- ottimizzati
- i
- Altro
- complessivo
- panoramica
- pacchetto
- parametri
- parte
- Platone
- Platone Data Intelligence
- PlatoneDati
- punto
- punti
- lavori
- possibile
- potente
- predire
- previsto
- predizione
- Previsioni
- presentata
- prezzo
- Prezzi
- prezzi
- Direttore
- principio
- Problema
- problemi
- purché
- Python
- quantità
- casuale
- Leggi
- lettori
- tempo reale
- realizzato
- ragione
- riconoscere
- Rosso
- di cui
- si riferisce
- regressione
- rapporto
- resti
- ricorda
- rappresentare
- rappresentazione
- rappresentato
- rappresenta
- riparazioni
- risorsa
- Ruolo
- Prenotazione sale
- stesso
- Scalabilità
- Scene
- Scienze
- scikit-impara
- Sezione
- sezioni
- set
- SGD
- spostamento
- dovrebbero
- mostrato
- Spettacoli
- Allo stesso modo
- Un'espansione
- singolo
- singolare
- Taglia
- pendenza
- piccole
- soluzione
- Soluzioni
- RISOLVERE
- alcuni
- qualcosa
- lo spazio
- velocità
- Squared
- piazze
- inizia a
- step
- Passi
- Ancora
- dritto
- La struttura
- tale
- suppone
- tavolo
- Fai
- Takeaways
- Target
- Task
- tecniche
- I
- Attraverso
- a
- Totale
- Training
- Alberi
- vero
- tipicamente
- sottostante
- capire
- Aggiornamenti
- us
- uso
- APPREZZIAMO
- Valori
- vario
- verificare
- visibile
- Che
- quale
- while
- volere
- parole
- utile
- sarebbe
- scrivere
- scritto
- X
- Trasferimento da aeroporto a Sharm
- zefiro
- zero