Comprendere gli intervalli di confidenza con Python

Questo articolo è stato pubblicato come parte di Blogathon sulla scienza dei dati.

Sommario

1. Introduzione
2. Intervalli di confidenza con statistica Z
3. Interpretazione degli intervalli di confidenza
4. Presupposti per CI usando la statistica z
5. Intervalli di confidenza con t-statistica
6. Assunzioni per CI usando la statistica t
7. Fare un t-intervallo con dati accoppiati
8. Valore z vs valore t: quando usare cosa?
9. Intervalli di confidenza con Python
10. Nota finale

Introduzione

Ogni volta che risolviamo un problema statistico ci preoccupiamo della stima dei parametri della popolazione, ma il più delle volte è quasi impossibile calcolare i parametri della popolazione. Quello che facciamo invece è prendere campioni casuali dalla popolazione e calcolare le statistiche del campione aspettandoci di approssimare i parametri della popolazione. Ma come facciamo a sapere se i campioni sono veri rappresentanti della popolazione o quanto queste statistiche campionarie si discostano dai parametri della popolazione? È qui che entrano in gioco gli intervalli di confidenza. Allora, quali sono questi intervalli? L'intervallo di confidenza è un intervallo di valori che vanno al di sopra e al di sotto delle statistiche campionarie oppure possiamo anche definirlo come la probabilità che un intervallo di valori attorno alla statistica campionaria contenga il parametro della popolazione reale.

Intervalli di confidenza con statistica Z

Prima di approfondire l'argomento, conosciamo alcune terminologie statistiche.

popolazione: È l'insieme di tutti gli individui simili. Ad esempio la popolazione di una città, gli studenti di un college, ecc.

campione: È un piccolo insieme di individui simili tratti dalla popolazione. Allo stesso modo, un campione casuale è un campione estratto a caso dalla popolazione.

parametri: media(mu), deviazioni standard(sigma), proporzione(p) derivata dalla popolazione.

statistica: media(x bar), deviazione std(S), proporzioni(p^) relative ai campioni.

Punteggio Z: è la distanza di qualsiasi punto di dati grezzi su una distribuzione normale dalla media normalizzata dalla deviazione std. Dato da: xmu/sigma

Bene, ora siamo pronti per approfondire il concetto di intervalli di confidenza. Per qualche ragione, credo che sia molto meglio comprendere i concetti attraverso esempi riconoscibili piuttosto che definizioni matematiche grezze. Quindi iniziamo.

supponiamo che tu viva in una città di 100,000 abitanti e che le elezioni siano dietro l'angolo. Come sondaggista, devi pronosticare chi vincerà le elezioni sia del partito blu che del giallo. Quindi, vedi che è quasi impossibile raccogliere informazioni dall'intera popolazione, quindi scegli a caso 100 persone. Alla fine del sondaggio, hai scoperto che il 62% delle persone voterà per il giallo. Ora la domanda è: dovremmo concludere che il giallo vincerà con una probabilità di vittoria del 62% o il 62% dell'intera popolazione voterà per il giallo? Bene, la risposta è no. Non sappiamo con certezza quanto sia lontana la nostra stima dal parametro vero, se prendiamo un altro campione il risultato potrebbe essere del 58% o del 65%. Quindi, ciò che faremo invece è trovare un intervallo di valori attorno alla nostra statistica campionaria che molto probabilmente catturerà la vera proporzione della popolazione. Qui, la proporzione si riferisce alla percentuale di

                                                                   l'immagine appartiene all'autore

Ora, se prendiamo un centinaio di tali campioni e tracciamo la proporzione campionaria di ciascun campione, otterremo una distribuzione normale delle proporzioni campionarie e la media della distribuzione sarà il valore più approssimativo della proporzione della popolazione. E la nostra stima potrebbe trovarsi in qualsiasi punto della curva di distribuzione. Secondo la regola 3-sigma, sappiamo che circa il 95% delle variabili casuali si trova entro 2 std deviazioni dalla media della distribuzione. Quindi, possiamo concludere che la probabilità che p^ è entro 2 std deviazioni di p è del 95%. Oppure possiamo anche affermare che la probabilità che p sia entro 2 std deviazioni sotto e sopra p^ è anch'essa del 95%. Queste due affermazioni sono effettivamente equivalenti. Questi due punti sotto e sopra p^ sono i nostri intervalli di confidenza.

                                                           l'immagine appartiene all'autore

Se riusciamo in qualche modo a trovare il sigma, possiamo calcolare il nostro intervallo richiesto. Ma qui sigma è il parametro della popolazione e sappiamo che spesso è quasi impossibile da calcolare, quindi useremo invece statistiche campione, ad esempio errore standard. Questo è dato come

dove p^= proporzione campionaria, n=numero di campioni

SE =√(0.62 . 0.38/100) = 0.05

quindi, 2xSE = 0.1

L'intervallo di confidenza per i nostri dati è (0.62-0.1,0.62+0.1) o (0.52,0.72). Poiché abbiamo preso 2xSE, questo si traduce in un intervallo di confidenza del 95%.

Ora, la domanda è cosa succede se vogliamo creare un intervallo di confidenza del 92%? Nell'esempio precedente, abbiamo moltiplicato 2 con SE per costruire un intervallo di confidenza del 95%, questo 2 è il punteggio z per un intervallo di confidenza del 95% (il valore esatto è 1.96) e questo valore può essere trovato da una tabella z. Il valore critico di z per un intervallo di confidenza del 92% è 1.75. Fare riferimento a questo articolo per una migliore comprensione di z-score e z-table.

L'intervallo è dato da: (p^ + z*.SE , p^-z*.SE).

Se invece della proporzione del campione viene fornita la media del campione, lo sarà l'errore standard sigma/quadrato(n). Qui sigma è la deviazione standard della popolazione poiché spesso non abbiamo, utilizziamo invece la deviazione standard del campione. Ma si osserva spesso che questo tipo di stima in cui viene data la media del risultato tende ad essere un po' distorta. Quindi, in casi come questo, è preferibile utilizzare la statistica t anziché la statistica z.

La formula generale per un intervallo di confidenza con statistica z è data da

Qui, la statistica si riferisce alla media campionaria o alla proporzione campionaria. sigma_s sono la deviazione standard della popolazione.

Interpretazione degli intervalli di confidenza

È molto importante interpretare correttamente gli intervalli di confidenza. Considera il precedente esempio di sondaggista in cui abbiamo calcolato che il nostro intervallo di confidenza del 95% fosse (0.52,0.62). Cosa significa? Bene, un intervallo di confidenza del 95% significa che se estraiamo n campioni dalla popolazione, il 95% delle volte l'intervallo derivato conterrà la vera proporzione della popolazione. Ricorda che un intervallo di confidenza del 95% non significa che esiste una probabilità del 95% che l'intervallo contenga la vera proporzione della popolazione. Ad esempio, per un intervallo di confidenza del 90%, se estraiamo 10 campioni da una popolazione, 9 volte su 10 tale intervallo conterrà il parametro della popolazione reale. Guarda l'immagine qui sotto per una migliore comprensione.

                                                            l'immagine appartiene all'autore

Assunzioni per intervalli di confidenza utilizzando la statistica Z

Ci sono alcune ipotesi che dobbiamo cercare per costruire un intervallo di confidenza valido usando la statistica z.

1. Campione casuale: i campioni devono essere casuali. Esistono diversi metodi di campionamento come campionamento stratificato, campionamento casuale semplice, campionamento a grappolo per ottenere campioni casuali.
2. Condizione normale: i dati devono soddisfare questa condizione np^>=10 e n.(1-p^)>=10. Ciò significa essenzialmente che la nostra distribuzione campionaria dei mezzi campionari deve essere normale, non distorta su entrambi i lati.
3. Indipendente: i campioni devono essere indipendenti. Il numero di campioni deve essere inferiore o uguale al 10% della popolazione totale o se il campionamento viene effettuato con sostituzione.

Intervalli di confidenza con statistica T

Cosa succede se la dimensione del campione è relativamente piccola e la deviazione standard della popolazione non è data o non può essere assunta? Come si costruisce un intervallo di confidenza? bene, è qui che entra in gioco la statistica t. La formula di base per trovare l'intervallo di confidenza qui rimane la stessa con solo z* sostituito da t*. La formula generale è data da

dove S = deviazione standard del campione, n = numero di campioni

Supponiamo di aver ospitato una festa e di voler stimare il consumo medio di birra dei tuoi ospiti. Quindi, ottieni un campione casuale di 20 individui e misura il consumo di birra. I dati del campione sono simmetrici con una media di 0f 1200 ml e una deviazione std di 120 ml. Quindi, ora desideri costruire un intervallo di confidenza del 95%.

Quindi, abbiamo la deviazione standard del campione, il numero di campioni e la media del campione. Tutto ciò di cui abbiamo bisogno è t*. Quindi, t* per un intervallo di confidenza del 95% con un grado di libertà di 19(n-1 = 20-1) è 2.093. Quindi, il nostro intervallo richiesto è dopo che il calcolo è (1256.16, 1143.83) con un margine di errore di 56.16. Fare riferimento a questo video per sapere come leggere la t-table.

Assunzioni per CI usando la statistica T

Simile al caso della statistica z qui, anche nel caso della statistica t ci sono alcune condizioni che dobbiamo cercare in dati dati.

1. Il campione deve essere casuale
2. Il campione deve essere normale. Per essere normale, la dimensione del campione dovrebbe essere maggiore o uguale a 30 o se il set di dati padre, ovvero la popolazione, è più o meno normale. Oppure, se la dimensione del campione è inferiore a 30, la distribuzione deve essere approssimativamente simmetrica.
3. Le osservazioni individuali devono essere indipendenti. Ciò significa che segue la regola del 10% o il campionamento viene eseguito con la sostituzione.

Creazione di un intervallo T per dati accoppiati

Finora abbiamo utilizzato solo dati di un campione. Ora vedremo come costruire un t-intervallo per dati appaiati. In dati appaiati, facciamo due osservazioni sullo stesso individuo. Ad esempio, confrontando i voti pre-test e post-test degli studenti o i dati sull'effetto di un farmaco e di un placebo su un gruppo di persone. Nei dati accoppiati, abbiamo trovato la differenza tra le due osservazioni nella terza colonna. Come al solito, faremo un esempio per comprendere anche questo concetto,

D. Un insegnante ha cercato di valutare l'effetto di un nuovo curriculum sul risultato del test. Di seguito i risultati delle osservazioni.

                                                      l'immagine appartiene all'autore

Poiché intendiamo trovare intervalli per la differenza media, abbiamo solo bisogno delle statistiche per le differenze. Useremo la stessa formula che abbiamo usato prima

statistica +- (valore critico o valore t) (deviazione standard della statistica)

x_d = media della differenza, S_d = deviazione std campionaria, per un IC al 95% con un grado di libertà 5 t* è dato da 2.57. Il margine di errore = 0.97 e l'intervallo di confidenza (4.18,6.13).

Interpretazione: Dalle stime di cui sopra come possiamo vedere l'intervallo di confidenza non contiene valori zero o negativi. Quindi, possiamo concludere che il nuovo curriculum ha avuto un impatto positivo sulle prestazioni dei test degli studenti. Se avesse solo valori negativi allora potremmo dire che il curriculum ha avuto un impatto negativo. Oppure, se conteneva zero, potrebbe esserci la possibilità che la differenza fosse zero o nessun effetto del curriculum sui risultati dei test.

Valore Z vs valore T

C'è molta confusione all'inizio su quando usare cosa. La regola pratica è quando la dimensione del campione è >= 30 ed è noto che la deviazione standard della popolazione utilizza le statistiche z. Nel caso in cui la dimensione del campione sia < 30, utilizzare la statistica t. Nella vita reale, non abbiamo parametri di popolazione, quindi andremo con z o t in base alla dimensione del campione.

Con campioni più piccoli (n<30) il teorema centrale LImit non si applica e viene utilizzata un'altra distribuzione chiamata distribuzione t di Student. La distribuzione t è simile alla distribuzione normale ma assume forme diverse a seconda della dimensione del campione. Invece dei valori z, vengono utilizzati valori t che sono più grandi per campioni più piccoli, producendo un margine di errore maggiore. Poiché una piccola dimensione del campione sarà meno precisa.

Intervalli di confidenza con Python

Python ha una vasta libreria che supporta tutti i tipi di calcoli statistici rendendoci la vita un po' più facile. In questa sezione, esamineremo i dati sulle abitudini del sonno dei bambini. I 20 partecipanti a queste osservazioni erano sani, si comportavano normalmente, non avevano alcun disturbo del sonno. Il nostro obiettivo è analizzare l'ora della nanna dei bambini che dormono e non fanno un pisolino.

Riferimento: Akacem LD, Simpkin CT, Carskadon MA, Wright KP Jr, Jenni OG, Achermann P, et al. (2015) I tempi dell'orologio circadiano e il sonno differiscono tra i bambini che sonnecchiano e quelli che non dormono. PLoS ONE 10(4): e0125181. https://doi.org/10.1371/journal.pone.0125181

Importeremo le librerie di cui avremo bisogno

import numpy as np import pandas as pd from scipy.stats import t pd.set_option('display.max_columns', 30) # imposta in modo da poter vedere tutte le colonne del DataFrame import math

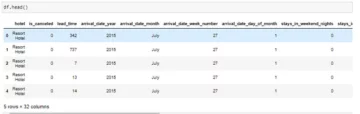
df = pd.read_csv(nap_no_nap.csv) #lettura dei dati

df.head ()

Crea due intervalli di confidenza al 95% per l'ora di andare a dormire media, uno per i bambini che fanno un pisolino e uno per i bambini che non lo fanno. Per prima cosa, isoleremo la colonna "notte di andare a dormire" per coloro che si sono addormentati in una nuova variabile e quelli che non hanno fatto un pisolino in un'altra nuova variabile. L'ora di andare a dormire qui è decimata.

bedtime_nap = df['night bedtime'].loc[df['napping'] == 1] bedtime_no_nap = df['night bedtime'].loc[df['napping'] == 0]

print(len(dormire_pisolino))

print(len(ora di andare a letto_no_nap))

uscita: 15 n 5

Ora troveremo l'ora di andare a dormire media di esempio per nap e no_nap.

nap_mean_bedtime = bedtime_no_nap.mean() #20.304 no_nap_mean_bedtime = bedtime_no_nap.mean() #19.59

Ora troveremo la deviazione standard campionaria per X_pisolino e X_{nessun pisolino} 

nap_s_bedtime = np.std(bedtime_nap,ddof=1) no_nap_s_bedtime = np.std(bedtime_no_nap,ddof=1)

Nota: il parametro ddof è impostato su 1 per sample std dev, altrimenti diventerà popolation std dev.

Ora troveremo l'errore standard di esempio per X_pisolino e X_{nessun pisolino} 

nap_se_mean_bedtime = nap_s_bedtime/math.sqrt(len(bedtime_nap)) #0.1526 no_nap_se_mean_bedtime = no_nap_s_bedtime/math.sqrt(len(bedtime_no_nap)) #0.2270

Fin qui tutto bene, ora poiché la dimensione del campione è piccola e non abbiamo una deviazione standard della proporzione della popolazione, utilizzeremo il valore t*. Un modo per trovare il valore t* è usare scipy.stats t.ppf funzione. Gli argomenti per t.ppf() sono q = percentuale, df = grado di libertà, scale = std dev, loc = media. Poiché la distribuzione t è simmetrica per un intervallo di confidenza del 95%, q sarà 0.975. Fare riferimento a questo per maggiori informazioni su t.ppf().

nap_t_star = t.ppf(0.975,df=14) #2.14 no_nap_t_star = t.ppf(0.975,df=5) #2.57

Ora aggiungeremo i pezzi per costruire finalmente il nostro intervallo di confidenza.

pisolino_ci_plus = pisolino_mean_andtime + pisolino_t_star*nap_se_andtime

pisolino_ci_minus = pisolino_mean_andare a dormire – pisolino_t_star*pisolino_se_ora di andare a dormire

stampa(nap_ci_minus,nap_ci_plus)

no_nap_ci_plus = no_nap_mean_andtime + no_nap_t_star*nap_se_andtime

no_nap_ci_minus = no_nap_mean_andtime – no_nap_t_star*nap_se_andtime

print(no_nap_ci_minus,no_nap_ci_plus)

uscita: 19.976680775477412 20.631319224522585 18.95974084563192 20.220259154368087

Interpretazione: 

Dai risultati di cui sopra, concludiamo che siamo sicuri al 95% che l'ora media di andare a dormire per i bambini piccoli è tra le 19.98:20.63 e le 18.96:20.22 (pm) mentre per i bambini che non fanno un pisolino è tra le XNUMX:XNUMX e le XNUMX:XNUMX (pm). Questi risultati sono secondo la nostra aspettativa che se fai un pisolino durante il giorno dormirai a tarda notte.

Note finali

Quindi, si trattava di semplici intervalli di confidenza che utilizzavano valori z e t. È davvero un concetto importante da conoscere nel caso di qualsiasi studio statistico. Un ottimo metodo statistico inferenziale per stimare i parametri della popolazione dai dati del campione. Gli intervalli di confidenza sono anche legati al test di ipotesi secondo cui per un IC al 95% si lascia il 5% di spazio per le anomalie. Se l'ipotesi nulla rientra nell'intervallo di confidenza, il valore p sarà grande e non saremo in grado di rifiutare null. Al contrario, se cade oltre, avremo prove sufficienti per rifiutare null e accettare ipotesi alternative.

Spero che l'articolo ti sia piaciuto e buon anno (:

I media mostrati in questo articolo non sono di proprietà di Analytics Vidhya e sono utilizzati a discrezione dell'autore.

Leggi Anche

Fonte: https://www.analyticsvidhya.com/blog/2022/01/understanding-confidence-intervals-with-python/