- 時系列は、一連の時間ベースの注文を表します。 それは年、月、週、日、ホルス、分、秒になります。
- 時系列は、連続する間隔の一連の離散時間からの観測です。
- 時系列は実行中のグラフです。
- 時間変数/特徴は独立変数であり、結果を予測するためのターゲット変数をサポートします。
- 時系列分析 (TSA) は、天気予報、金融、信号処理、エンジニアリング領域 - 制御システム、通信システムなど、時間ベースの予測のさまざまな分野で使用されています。
- TSA は特定のシーケンスで一連の情報を生成することを伴うため、空間分析やその他の分析とは異なります。
- AR、MA、ARMA、ARIMA モデルを使用すると、未来を予測できます。
時系列分析の概要
時系列分析は、時間に対する応答変数の特性を独立変数として研究する方法です。 予測または予想という名目でターゲット変数を推定するには、時間変数を基準点として使用します。 この記事では、TSA の目的、前提条件、コンポーネント (定常および非定常) について詳しく説明します。 TSA アルゴリズムと Python の特定の使用例も併せて説明します。
-
時系列分析 (TSA) とその前提とは何ですか
- 分析方法)?
- 時系列分析の意義とその種類
- 時系列のコンポーネント
- 時系列の制限は何ですか?
- 時系列データ型の詳細な研究。
- 固定コンポーネントと非固定コンポーネントに関するディスカッション
- 非定常から定常への変換
- 時系列分析がデータ サイエンスと機械学習で使用されるのはなぜですか?
- データサイエンスと機械学習における時系列分析
- 自己回帰モデルの実装
- 移動平均の実装 (WEIGHTS – SIMPLE MOVING AVERAGE)
- ARMA と ARIMA を理解する
- ARIMA の実装手順
- 時系列分析 – プロセス フロー (Re-gap)
時系列分析とは
定義: ご覧のとおり、TSA にはさらに多くの定義があります。 ただし、シンプルにしてください。
時系列とは、一定期間に連続して発生したさまざまなデータ ポイントのシーケンスに他なりません。
目的:
- 時系列がどのように機能するか、さまざまな時点で特定の変数にどのような要因が影響を与えているかを理解するために。
- 時系列分析は、時間の経過とともに変化する特定のデータセットの特徴の結果と洞察を提供します。
- 時系列変数の将来の値を予測して導出するのをサポートします。
- 仮定: 「定常」な仮定が XNUMX つだけあります。これは、時間の起源が統計的要因に基づくプロセスの特性に影響を与えないことを意味します。
時系列を分析するにはどうすればよいですか?
とにかく、参考までにここに簡単な手順を示します。 これについては、後ほどこの記事で詳しく説明します。
- データの収集とクリーニング
- 時間と主要な機能に関する視覚化の準備
- 系列の定常性の観察
- その性質を理解するためにチャートを作成します。
- モデル構築 – AR、MA、ARMA、ARIMA
- 予測から洞察を抽出する
時系列の意味とその種類
TSA は、時間ベースの問題ステートメントに特有の、予測および予測分析のバックボーンです。
- 過去のデータセットとそのパターンの分析
- 現在の状況を理解し、前段階から導き出されたパターンと照合します。
- さまざまな期間における特定の変数に影響を与える要因を理解する。
「時系列」の助けを借りて、多数の時間ベースの分析と結果を準備できます。
- 予測分析
- Segmentation
- Classification
- 記述的分析`
- 介入分析
時系列分析のコンポーネント
- トレンド
- 季節性
- 循環
- 不規則性
- トレンド: 固定間隔はなく、特定のデータセット内の発散は連続的なタイムラインです。 トレンドはネガティブ、ポジティブ、またはヌルトレンドになります。
- 季節性: 連続タイムライン内のデータセット内で定期的または固定間隔がシフトします。 ベルカーブかノコギリ歯でしょう
- 循環: 一定の間隔がなく、動きとそのパターンが不確実である
- 不規則性: 予期せぬ状況、イベント、シナリオ、および短期間での急増。

時系列分析の制限は何ですか?
時系列には以下の制限があるため、分析中にそれらの制限に注意する必要があります。
- 他のモデルと同様に、欠損値は TSA によってサポートされません。
- データ ポイントの関係は線形である必要があります。
- データ変換が必須なので、少々費用がかかります。
- モデルは主に単変量データで動作します。
時系列のデータ型
時系列のデータ型とその影響について説明します。 TS データ型について説明しますが、主に XNUMX つの型があります。
- 定常
- 非定常
6.1 定常: データセットは、時系列の傾向、季節性、周期性、不規則性のコンポーネントを持たずに、以下の経験則に従う必要があります。
- それらの平均値は、分析中のデータ内で完全に一定である必要があります。
- VARIANCE は時間枠に関して一定である必要があります
- COVARIANCE は、XNUMX つの変数間の関係を測定します。
6.2 非定常y:これはStationaryの真逆ですね。

定常性を確認する方法
TSA モデルの準備ワークフロー中に、指定されたデータセットが静止しているかどうかにアクセスする必要があります。 使用する 統計テストとプロットテスト。
7.1 統計的テスト: データセットが静止しているかどうかをテストするために使用できるテストが XNUMX つあります。
- 拡張ディッキー・フラー (ADF) テスト
- クウィアトコウスキー・フィリップス・シュミット・シン (KPSS) テスト
7.1.1 拡張ディッキー・フラー (ADF) テストまたはユニット ルート テスト: ADF テストは最も一般的な統計テストであり、次の前提があります。
- 帰無仮説 (H0): シリーズは非定常です
- 代替仮説 (HA): 系列は定常である
- p 値 >0.05 拒否に失敗 (H0)
- p 値 <= 0.05 許容 (H1)
7.1.2 クウィアトコウスキー – フィリップス – シュミット – シン (KPSS): これらのテストは、帰無仮説 (HO) をテストするために使用されます。この仮説は、単位根の代替に対して決定論的な傾向の周りで時系列が定常であると認識します。 TSA はさらなる分析のために定常データを探しているため、データセットが定常であることを確認する必要があります。
非定常から定常への変換
効果的な時系列モデリングのために非定常を定常に変換する方法を簡単に説明します。 この変換には主に XNUMX つの方法が利用できます。
- トレンド除去
- 差分
- 変換
8.1 トレンド除去: これには、特定のデータセットから傾向の影響を削除し、傾向との値の差のみを表示することが含まれます。 これにより、常に周期的なパターンを識別できるようになります。

8.2 相違点: これは、系列を新しい時系列に単純に変換するもので、系列の時間への依存を取り除き、時系列の平均を安定させるために使用します。これにより、この変換中に傾向と季節性が軽減されます。
Yt= Yt – Yt-1
Yt=時間経過に伴う値
トレンド除去と差分抽出

8.3 変換: これには、べき乗変換、平方根、対数転送という XNUMX つの異なる方法が含まれます。最も一般的に使用されるのは対数転送です。
移動平均法
一般的に使用される時系列手法は移動平均です。 この方法は、ランダムな短期変動を伴う巧妙な方法です。 時系列のコンポーネントと相対的に関連付けられます。
移動平均 (MA) (または) 移動平均: ここで MA は、k 期間内の時系列のデータを平均することによって計算されます。
移動平均の種類を見てみましょう。
- 単純移動平均 (SMA)、
- 累積移動平均 (CMA)
- 指数移動平均(EMA)
9.1 単純移動平均 (SMA)
SMA は、前の M または N ポイントの重み付けされていない平均です。 M または N の値を増やすと精度が犠牲になって平滑化が向上するため、平滑化の量に応じてスライディング ウィンドウ データ ポイントを選択することが推奨されます。

よりよく理解するには、気温を使用します。
matplotlib から pd としてパンダをインポート statsmodels.graphics.tsaplots から pyplot を plt としてインポート import Lot_acf df_temperature = pd.read_csv('temperature_TSA.csv', encoding='utf-8') df_temperature.head()

df_温度.info()

# 年の列のインデックスを設定します df_temperature.set_index('Any', inplace=True) df_temperature.index.name = 'year' # 年間平均気温 - 計算 df_temperature['average_temperature'] = df_temperature.mean(axis=1) #不要な列を削除し、データフレームをリセットします。 df_temperature = df_temperature[['average_temperature']] df_temperature.head()

# 10 年と 20 年の期間にわたる SMA df_temperature['SMA_10'] = df_temperature.average_temperature.rolling(10, min_periods=1).mean() df_temperature['SMA_20'] = df_temperature.average_temperature.rolling(20, min_periods=) 1).mean()
# 緑 = 平均気温、赤 = 10 年、折れ線グラフのオレンジ色 color = ['green', 'red', 'orange'] # 折れ線グラフ df_temperature.plot(color=colors, linewidth=3, figsize= (12,6)) plt.xticks(fontsize=14) plt.yticks(fontsize=14) plt.legend(labels =['平均気温', '10 年 SMA', '20 年 SMA'], fontsize=14) plt.title('都市の年間平均気温', fontsize=20) plt.xlabel('年', fontsize=16) plt.ylabel('気温 [℃]', fontsize=16)

9.2 累積移動平均 (CMA)
CMA は、現在までの過去の値の加重なし平均です。

# CMA 気温 df_tempor['CMA'] = df_temperature.average_temperature.expanding().mean()
# 緑 - 平均気温とオレンジ - CMA 色 = ['green', 'orange'] # 折れ線グラフ df_temperature[['average_temperature', 'CMA']].plot(color=colors, linewidth=3, figsize=( 12,6)) plt.xticks(fontsize=14) plt.yticks(fontsize=14) plt.legend(labels =['平均気温', 'CMA'], fontsize=14) plt.title('年間都市の平均気温', fontsize=20) plt.xlabel('年', fontsize=16) plt.ylabel('気温 [°C]', fontsize=16)

9.3 指数移動平均 (EMA)
EMA は主に傾向を特定し、ノイズを除去するために使用されます。 要素の重量は時間の経過とともに徐々に減少します。 これは、過去のデータ ポイントではなく、最近のデータ ポイントに重みを与えることを意味します。 SMA と比較して、EMA は変化が速く、より敏感です。
α –> 平滑化係数。
- 値は 0,1 から XNUMX の間です。
- ごく最近の期間に適用される重み付けを表します。
与えられたデータセットに平滑化係数 0.1 と 0.3 を使用して指数移動平均を適用してみましょう。

# EMA 気温 # 平滑化係数を考えてみましょう - 0.1 df_temperature['EMA_0.1'] = df_temperature.average_temperature.ewm(alpha=0.1,Adjust=False).mean() # 平滑化係数を考えてみましょう - 0.3 df_temperature['EMA_0.3' ] = df_温度.平均温度.ewm(alpha=0.3、adjust=False).mean()
# 緑 - 平均気温、赤 - 平滑化係数 - 0.1、黄 - 平滑化係数 - 0.3 色 = ['緑', '赤', '黄色'] df_temperture[['平均温度', 'EMA_0.1', 'EMA_0.3 .3']].plot(color=colors, linewidth=12,6, figsize=(0.8), alpha=14) plt.xticks(fontsize=14) plt.yticks(fontsize=0.1) plt.legend(labels= ['平均気温', 'EMA - alpha=0.3', 'EMA - alpha=14'], fontsize=20) plt.title('都市の年間平均気温', fontsize=16) plt.xlabel( '年', fontsize=16) plt.ylabel('温度 [°C]', fontsize=XNUMX)

データサイエンスと機械学習における時系列分析
データ サイエンスと機械学習で TSA を扱う場合、複数のモデル オプションが利用可能です。 ここでは、[p、d、q] を使用した自己回帰移動平均 (ARMA) モデルが使用されます。
- P==> 自己回帰ラグ
- q== 移動平均の遅れ
- d==> 順序の違い
有馬について知る前に、まず以下の用語をよく理解する必要があります。
- 自己相関関数 (ACF)
- 部分自己相関関数 (PACF)
10.1 自己相関関数 (ACF): ACF は、特定の時系列内の値と前の値がどの程度類似しているかを示すために使用されます。 (OR) 特定の時系列と、観察したさまざまな間隔でのその時系列の時間差バージョンとの間の類似性の程度を測定します。
Python Statsmodels ライブラリは自己相関を計算します。 これは、特定のデータセット内の一連の傾向と、以前の観測値が現在観測されている値に及ぼす影響を特定するために使用されます。
10.2 部分自己相関 (PACF): PACF は自己相関関数に似ており、理解するのが少し困難です。 これは、直接効果のみが示され、他のすべての中間効果が指定された時系列から削除された、シーケンス順序ごとに一定の時間単位を使用してシーケンスとそれ自体の相関関係を常に示します。
自己相関と部分自己相関
プロット_acf(df_温度) plt.show()
プロット_acf(df_温度、ラグ=30) plt.show()

観察: 以前の温度は現在の温度に影響を与えますが、その影響の重要性は、一定の時間間隔での温度とともに上記の視覚化から減少し、わずかに増加します。
10.3 自己相関の種類

10.4 ACF および PACF プロットの解釈
| ACF |
PACF |
パーフェクト ML -モデル |
| プロットは徐々に衰退します | プロットは即座に削除されます | 自動回帰モデル。 |
| プロットは即座に削除されます | プロットは徐々に衰退します | 移動平均モデル |
| 徐々に衰退していくプロット | プロットは徐々に衰退します | ARMA |
| プロットは即座に削除されます | プロットは即座に削除されます | あなたはどんなモデルも演じないでしょう |
ACF と PACF の両方で、分析には定常時系列が必要であることに注意してください。
さて、私たちはについて学びます 自己回帰モデル
これは、過去のパフォーマンスに基づいて将来のパフォーマンスを予測する単純なモデルです。 主に、特定の時系列の値と前後 (前後) の値との間に相関関係がある場合の予測に使用されます。
AR モデルは、遅延変数を入力として使用する線形回帰モデルです。 線形回帰モデルは、scikit-learn ライブラリを使用して、使用する入力を指定することで簡単に構築できます。 Statsmodels ライブラリは、適切なラグ値を指定してモデルをトレーニングする必要がある自己回帰モデル固有の関数を提供するために使用されます。 簡単な手順を使用して結果を取得するために、AutoTeg クラスで提供されます。
AR モデルの方程式 (Y=mX+c を比較してみましょう)
Yt =C+b1 YT-1+ B2 YT-2+……+bp YTP+えーt
主要なパラメータ
- p=過去の値
- Yt=異なる過去の値の関数
- Ert=時間の誤差
- C=切片
与えられたデータセットまたは時系列がランダムかどうかを確認してみましょう
matplotlib から import pyplot from pandas.plotting import lag_plot lag_plot(df_temperur) pyplot.show()

観察: はい、ランダムでバラバラに見えます。
自己回帰モデルの実装
#matplotlib からライブラリをインポート import pyplot from statsmodels.tsa.ar_model import AutoReg from sklearn.metrics import means_squared_error from math import sqrt # CSV をデータセットとしてロード #series = read_csv('daily-min-temperatures.csv', header=0, Index_col =0、parse_dates=True、squeeze=True) # テストとトレーニング用にデータセットを分割 X = df_temperature.values train, test = X[1:len(X)-7], X[len(X)-7:] #自己回帰モデルのトレーニング = AutoReg(train, lags=20) model_fit = model.fit() print('Coefficients: %s' % model_fit.params) # 予測予測 = model_fit.predict(start=len(train), end=len) (train)+len(test)-1、dynamic=False) for i in range(len(predictions)): print('predicted=%f, Expected=%f' % (predictions[i], test[i] )) rmse = sqrt(mean_squared_error(test, precision)) print('Test RMSE: %.3f' % rmse) # プロット結果 pyplot.plot(test) pyplot.plot(predictions, color='red') pyplot.show ()
出力
予測=15.893972、期待=16.275000 予測=15.917959、期待=16.600000 予測=15.812741、期待=16.475000 予測=15.787555、期待=16.375000 予測=16.023780、期待=16.283333 予測=15.940271 16.525000、期待値=15.831538 予測値=16.758333、期待値=0.617 テストRMSE: XNUMX

観察: 予想 (青) 対 予想 (赤)。 4日目は予報が良くなり、6日目は乖離が見られます。
移動平均の実装 (WEIGHTS – SIMPLE MOVING AVERAGE)
import numpy as np alpha= 0.3 n = 10 w_sma = np.repeat(1/n, n) Colors = ['green', ' yellow'] # 重み - 指数移動平均 alpha=0.3Adjust=False w_ema = [(1 -ALPHA)**i if i==N-1 else alpha*(1-alpha)**i for i in range(n)] pd.DataFrame({'w_sma': w_sma, 'w_ema': w_ema}) .plot(color=colors, kind='bar', figsize=(8,5)) plt.xticks([]) plt.yticks(fontsize=10) plt.legend(labels=['単純移動平均', '指数移動平均 (α=0.3)'], fontsize=10) # タイトルとラベル plt.title('Moving Average Weights', fontsize=10) plt.ylabel('Weights', fontsize=10)

ARMA と ARIMA を理解する
ARMA これは、予測用の自動回帰モデルと移動平均モデルを組み合わせたものです。 このモデルは、XNUMX つの多項式 (XNUMX つは自動回帰用、もう XNUMX つは移動平均用) に関して弱定常確率過程を提供します。

ARMA 定常系列を予測するのに最適です。 そこで、固定と非固定をサポートする ARIMA が登場しました。

AR+I+MA= アリマ
ARIMAの特徴を理解する
- p==> 対数順序 => ラグ観測の数。
- d==> 差異の程度 => 生の観測値が差異化された回数。
- q==>移動平均の次数 => 移動平均ウィンドウのサイズ
ARIMA の実装手順
ステップ 1: 時系列形式をプロットする
ステップ 2: 傾向を削除して平均値で差を固定する
ステップ 3: 対数変換を適用して定常状態にします。
ステップ 4: 統計平均と分散の両方で定常として行う差分対数変換
ステップ 5: ACF および PACF をプロットし、潜在的な AR および MA モデルを特定する
ステップ 6: 最適な ARIMA モデルの発見
ステップ 7: 最適な ARIMA モデルを使用して値を予測/予測する
ステップ 8: ARIMA モデルの残差について ACF および PACF をプロットし、それ以上の情報が残っていないことを確認します。
ARIMAの実装
すでにステップ 1 ~ 5 について説明しましたが、ここでは残りの部分に焦点を当てましょう。
statsmodels.tsa.arima_model からインポート ARIMA モデル = ARIMA(df_temperature, order=(0, 1, 1)) results_ARIMA = model.fit()
results_ARIMA.summary()

results_ARIMA.forecast(3)[0]
出力
配列([16.47648941, 16.48621826, 16.49594711])
results_ARIMA.plot_predict(start=200) plt.show()

(再ギャップ)


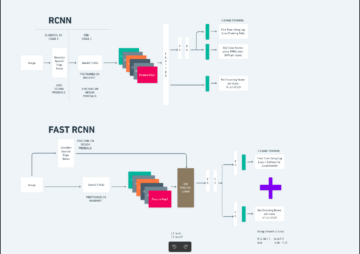
リカレント ニューラル ネットワークは、 最も伝統的で受け入れられているアーキテクチャであり、時系列予測ベースの問題に適合します。
RNN は連続した層に編成され、次のように分割されます。
- 入力
- 隠されました
- 出力
各層の重みは等しいため、すべてのニューロンを固定のタイム ステップに割り当てる必要があります。 そして、それらのすべてが同じタイム ステップの隠れ層 (入力と出力) に完全に接続されており、隠れ層は転送され、方向が時間に依存することを覚えておいてください。

RNN のコンポーネント
- 入力: x(t) の関数ベクトルは、タイム ステップ t での入力です。
-
隠し:
- 関数ベクトル h(t) は時間 t における隠れ状態であり、
- これは確立されたネットワークの一種の記憶です。
- これは、現在の入力 x(t) と前回のステップの隠れ状態 h(t-1) に基づいて計算されています。
- 出力: 関数ベクトル y(t) は、タイム ステップ t での出力です。
- 重み : 重み: RNN では、時間 t で隠れ層ニューロンに接続された入力ベクトルは次のようになります。 の重み行列によって U (上の写真を参照してください)、
内部重み付けマトリックス W は、時間 t-1 と t+1 の隠れ層ニューロンによって形成されます。 これに、時間 t の出力ベクトル y(t) に対する隠れ層が続きます。 V (重みマトリックス); すべての重み行列 U、W、V は各タイム ステップで一定です。
| Advantages | デメリット |
| RNN はあらゆる情報をすべて記憶するという特徴があるため、時系列予測に非常に役立ちます。 | 大きな課題はトレーニング期間中です。 |
| 入力時系列データセットから複雑なパターンを作成するのに最適です。 | 高価な計算コスト |
| 予測/予測が速い | |
| 欠損値の影響を受けないため、クレンジングプロセスを制限できます |
このガイドは、皆さんが時系列、流れ、仕組みを理解するのに役立つと信じています。
この記事に示されているメディアは Analytics Vidhya が所有するものではなく、著者の裁量で使用されています。
出典: https://www.analyticsvidhya.com/blog/2021/10/a-comprehensive-guide-to-time-series-analysis/
- "
- &
- 11
- 7
- 9
- アクセス
- アルゴリズム
- すべて
- 分析
- 分析論
- AR
- 建築
- 周りに
- 記事
- オート
- AVG
- ベル
- BEST
- 建物
- これ
- 例
- 挑戦する
- 変化する
- チャート
- 市町村
- クリーニング
- コラム
- 通信部
- コンポーネント
- 変換
- 作成
- 電流プローブ
- 曲線
- データ
- データサイエンス
- 中
- 取引
- 深い学習
- 詳細
- 発見
- Drop
- 効果的な
- EMA
- エンジニアリング
- 特徴
- 特徴
- フィールズ
- ファイナンシャル
- 名
- フィット
- フロー
- フォーカス
- function
- 未来
- 良い
- グリーン
- ガイド
- こちら
- 認定条件
- How To
- HTTPS
- 識別する
- 画像
- index
- 影響
- 情報
- 洞察
- IT
- キー
- ラベル
- LEARN
- 学習
- 図書館
- LINE
- 負荷
- 機械学習
- 主要な
- math
- マトリックス
- メディア
- メトリック
- ML
- モデリング
- ヶ月
- 一番人気
- ネットワーク
- ネットワーク
- ニューラル
- ニューラルネットワーク
- ノイズ
- オプション
- 注文
- 受注
- その他
- パフォーマンス
- 画像
- 人気
- 電力
- 予測
- 予測
- Python
- Raw
- 回帰
- 応答
- REST
- 結果
- ルール
- ランニング
- 科学
- シリーズ
- セッションに
- ショート
- 簡単な拡張で
- サイズ
- So
- 空間の
- split
- 広場
- ステージ
- 勉強
- サポート
- サポート
- システム
- ターゲット
- test
- テスト
- テスト
- 未来
- 時間
- トレーニング
- 変換
- トレンド
- 値
- 可視化
- W
- 以内
- 仕事
- ワークフロー
- 作品
- X
- 年
- 年