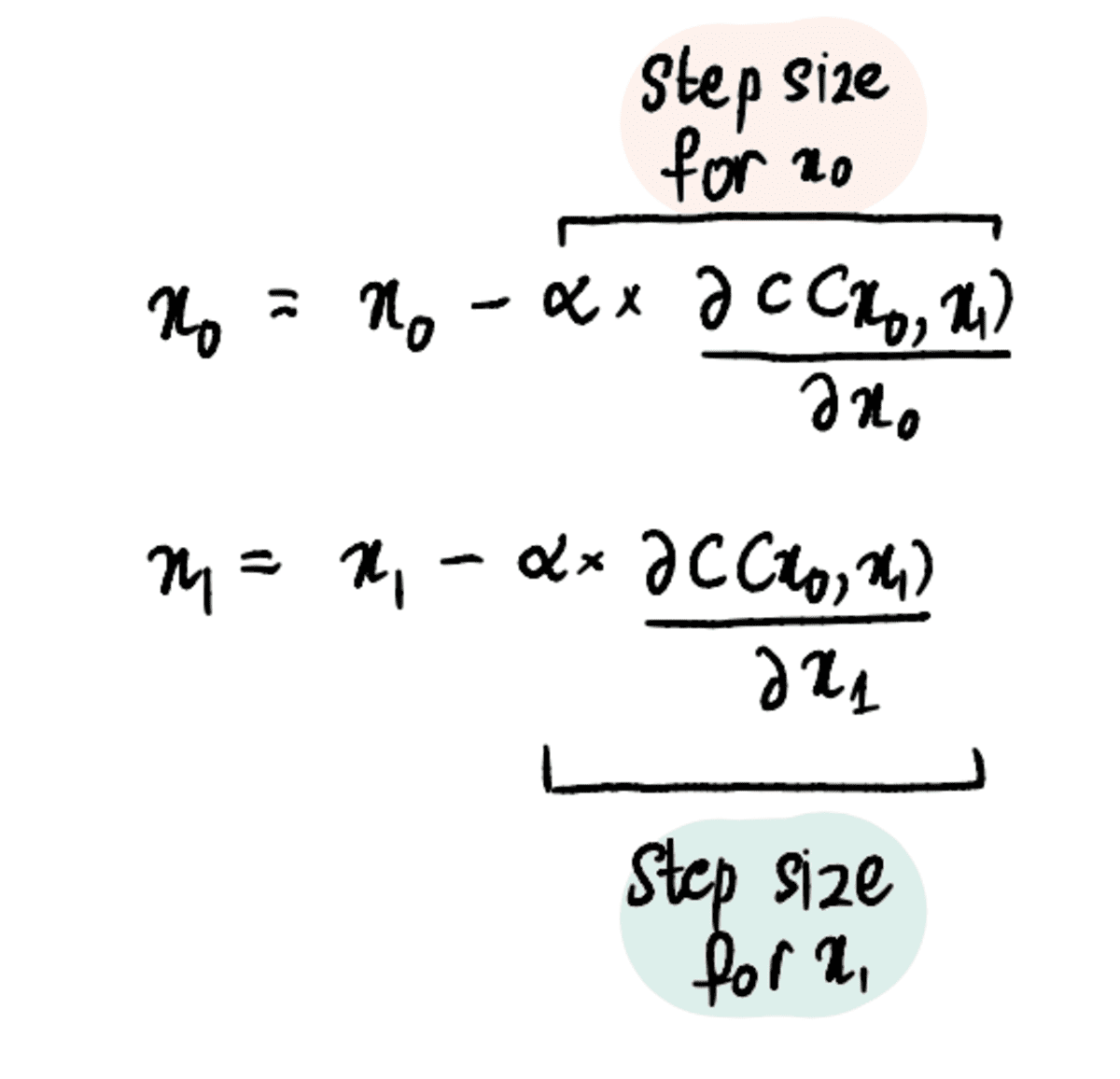Back to Basics, Part Dos: Gradient Descent

Welkom bij het tweede deel van onze Terug naar de basis serie. In de eerste deel, hebben we besproken hoe lineaire regressie en kostenfunctie kunnen worden gebruikt om de best passende lijn voor onze huisprijsgegevens te vinden. We zagen echter ook dat het testen van meerdere onderscheppen waarden kunnen vervelend en inefficiënt zijn. In dit tweede deel gaan we dieper in op Gradient Descent, een krachtige techniek die ons kan helpen het perfecte te vinden onderscheppen en ons model optimaliseren. We zullen de wiskunde erachter onderzoeken en zien hoe deze kan worden toegepast op ons lineaire regressieprobleem.

Gradiëntafdaling is een krachtig optimalisatie-algoritme dat heeft tot doel snel en efficiënt het minimumpunt van een curve te vinden. De beste manier om dit proces te visualiseren, is door je voor te stellen dat je op de top van een heuvel staat, met een schatkist gevuld met goud die op je wacht in de vallei.

 

 

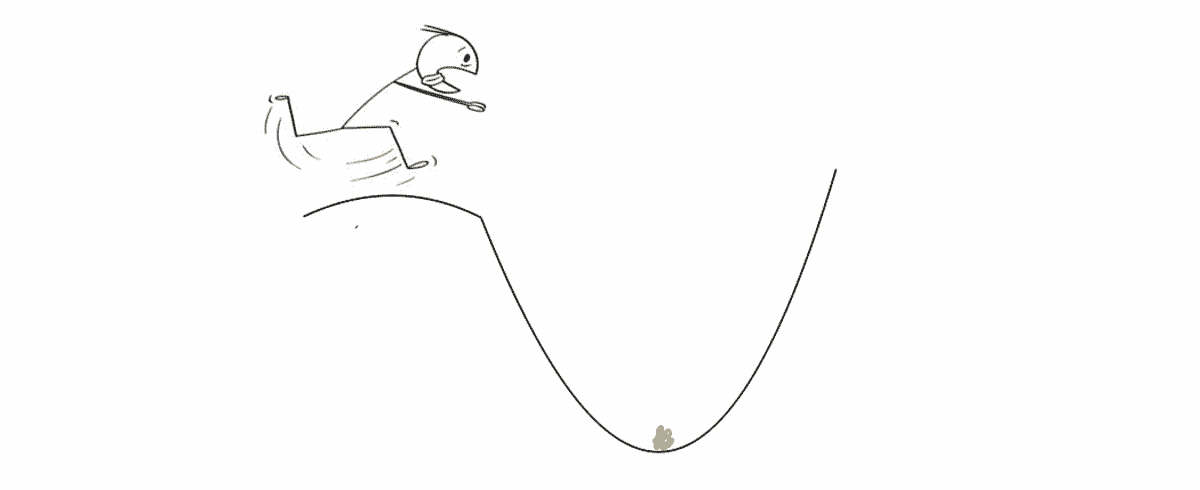
De exacte locatie van de vallei is echter onbekend omdat het buiten superdonker is en je niets kunt zien. Bovendien wil je de vallei bereiken voordat iemand anders dat doet (omdat je alle schatten voor jezelf wilt duh). Gradiëntafdaling helpt je om door het terrein te navigeren en dit te bereiken optimale punt efficiënt en snel. Op elk punt zal het je vertellen hoeveel stappen je moet nemen en in welke richting je ze moet nemen.

Evenzo kan gradiëntafdaling worden toegepast op ons lineaire regressieprobleem door de stappen te gebruiken die door het algoritme zijn uiteengezet. Laten we, om het proces van het vinden van het minimum te visualiseren, de grafiek uitzetten MSE kromme. We weten al dat de vergelijking van de kromme is:

 

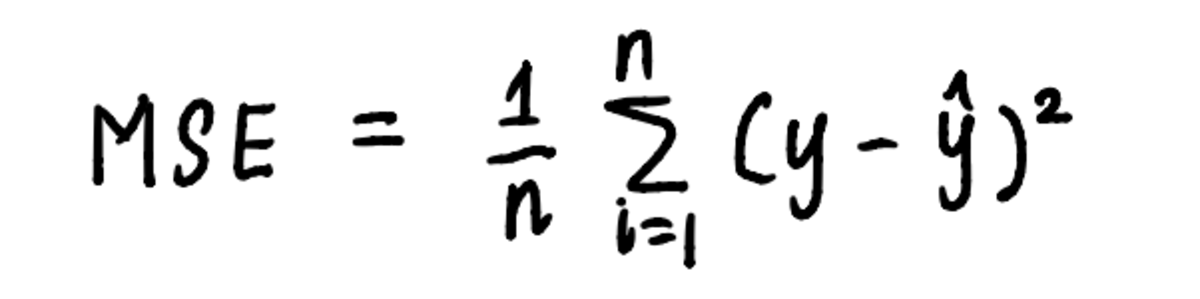
de vergelijking van de curve is de vergelijking die wordt gebruikt om de MSE te berekenen

 

En van de vorige artikel, we weten dat de vergelijking van MSE in ons probleem is:

 

 

Als we uitzoomen kunnen we zien dat een MSE curve (die lijkt op onze vallei) kan worden gevonden door een aantal te vervangen onderscheppen waarden in de bovenstaande vergelijking. Dus laten we 10,000 waarden van de inpluggen onderscheppen, om een ​​curve te krijgen die er zo uitziet:

 

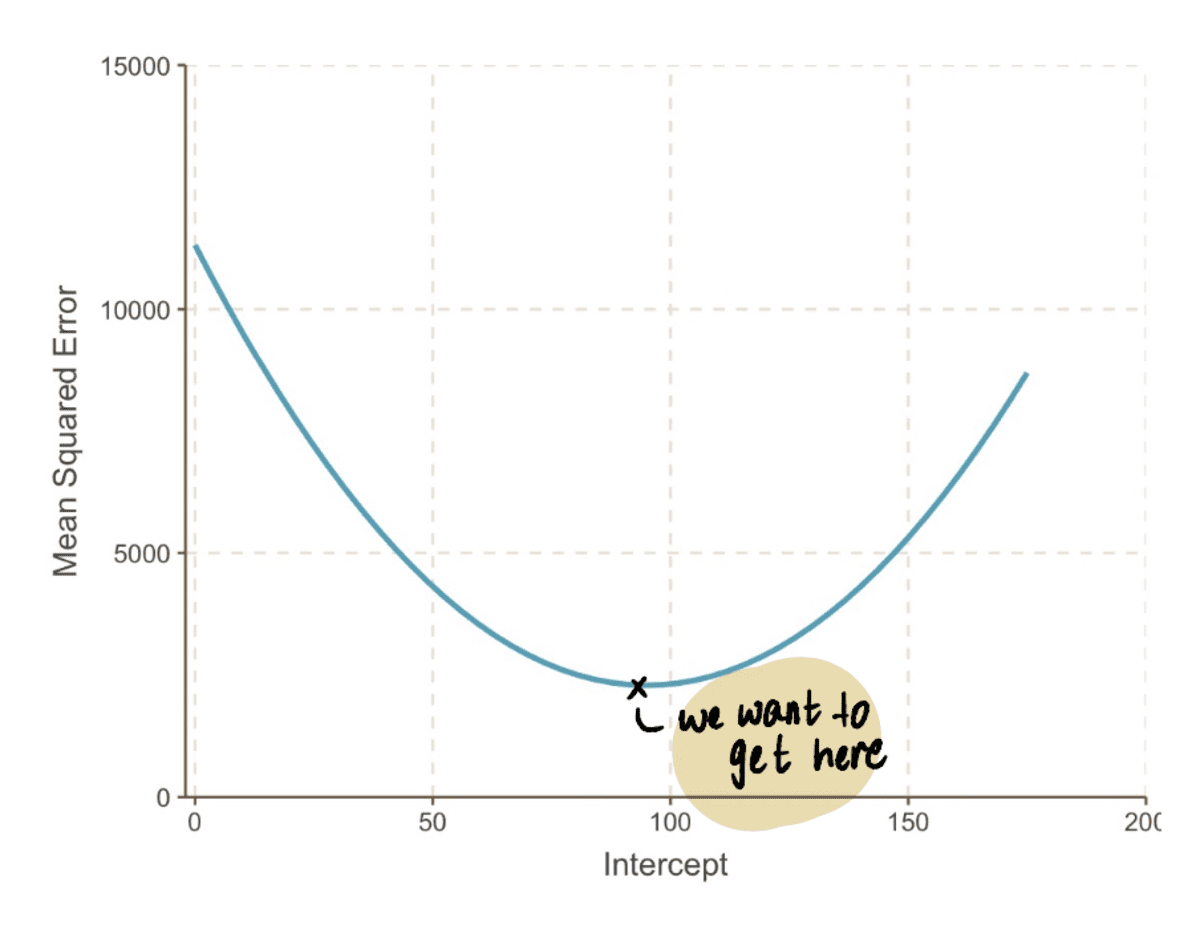
in werkelijkheid zullen we niet weten hoe de MSE-curve eruit ziet

 

Het doel is om de bodem hiervan te bereiken MSE curve, wat we kunnen doen door deze stappen te volgen:

Stap 1: Begin met een willekeurige initiële gok voor de onderscheppingswaarde

Laten we in dit geval uitgaan van onze eerste gok voor de onderscheppen waarde is 0.

Stap 2: Bereken de helling van de MSE-curve op dit punt

De gradient van een curve op een punt wordt weergegeven door de raaklijn (een mooie manier om te zeggen dat de lijn de curve alleen op dat punt raakt) op dat punt. Bijvoorbeeld bij punt A, de gradient van de MSE curve kan worden weergegeven door de rode raaklijn, wanneer het snijpunt gelijk is aan 0.

 

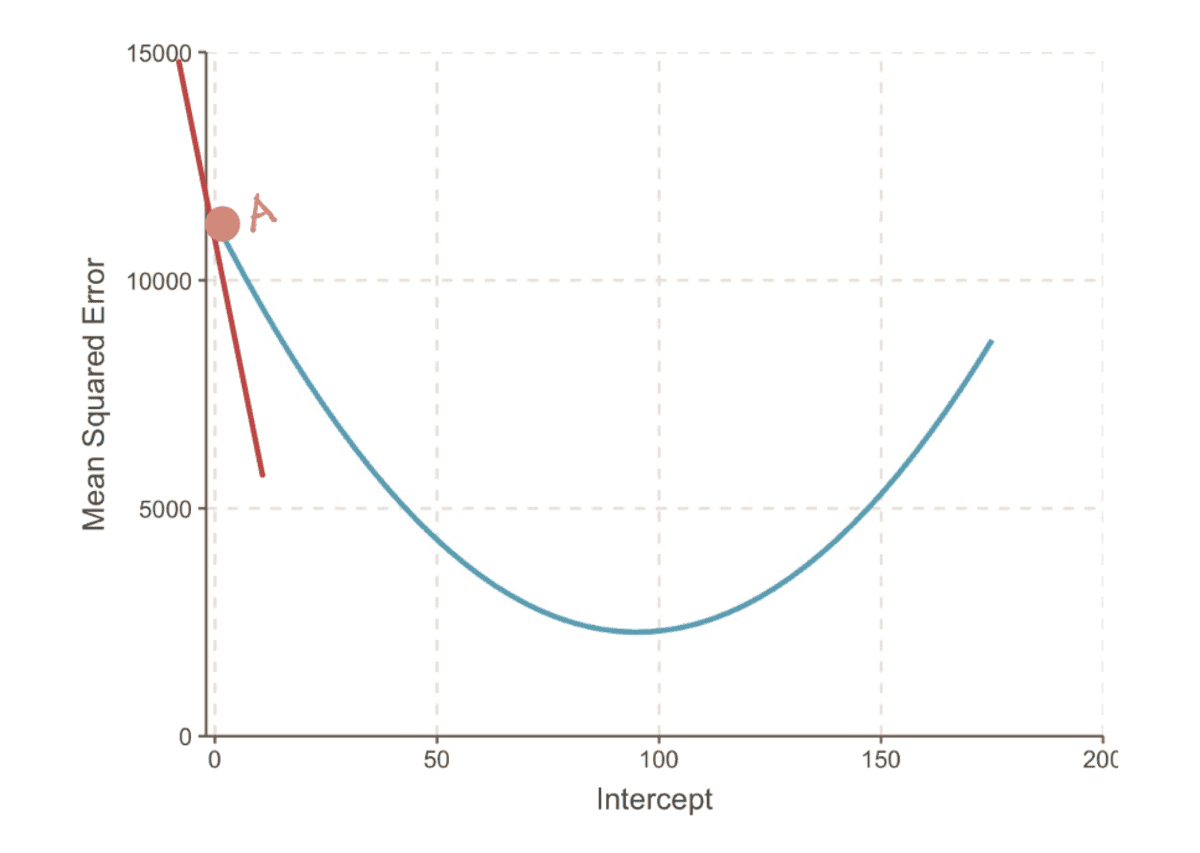
de gradiënt van de MSE-curve wanneer onderschepping = 0

 

Om de waarde van de gradient, passen we onze kennis van calculus toe. Met name de gradient is gelijk aan de afgeleide van de kromme ten opzichte van de onderscheppen op een gegeven moment. Dit wordt aangeduid als:

 

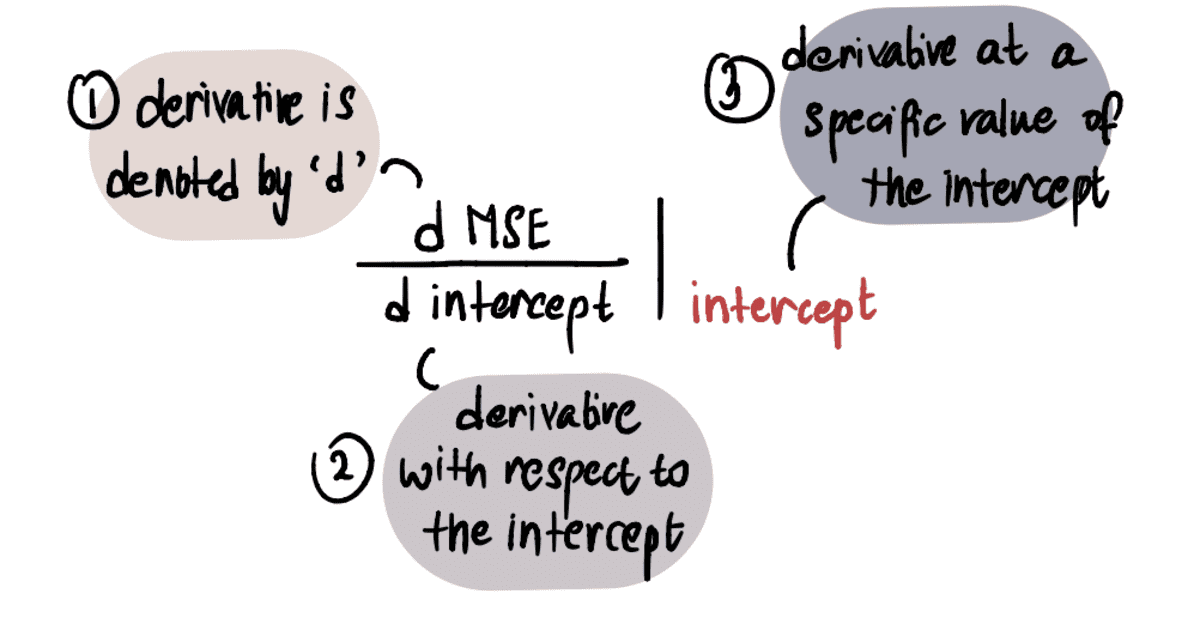
LET OP: Als je niet bekend bent met derivaten, raad ik je aan dit te bekijken Khan Academy-video indien geïnteresseerd. Anders kunt u het volgende deel overslaan en toch de rest van het artikel volgen.

We berekenen de afgeleide van de MSE-curve als volgt:

 

 

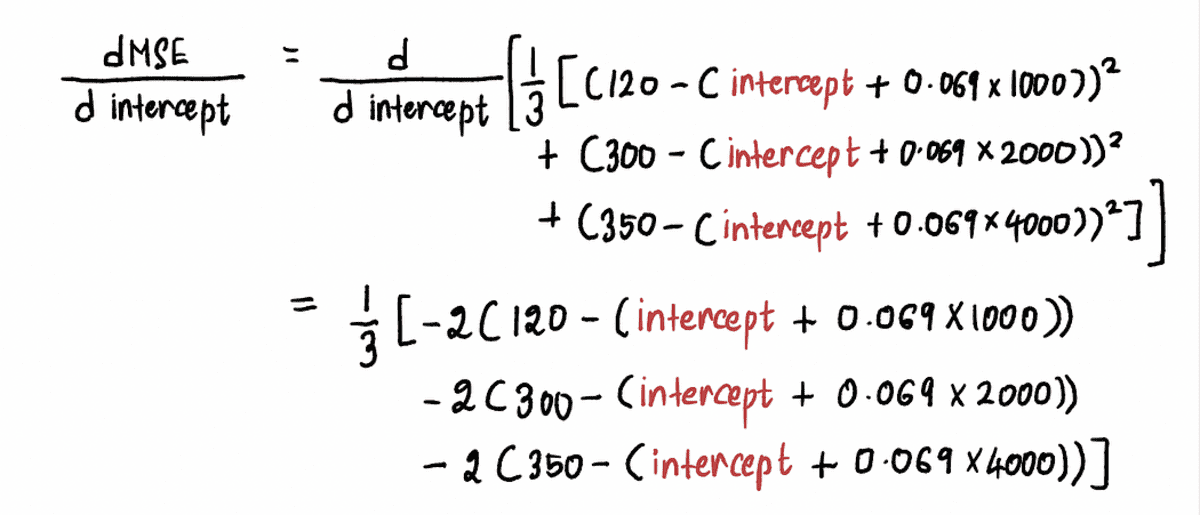
Nu nog de vinden verloop bij punt A, vervangen we de waarde van de onderscheppen op punt A in de bovenstaande vergelijking. Sinds onderscheppen = 0, de afgeleide in punt A is:

 

 

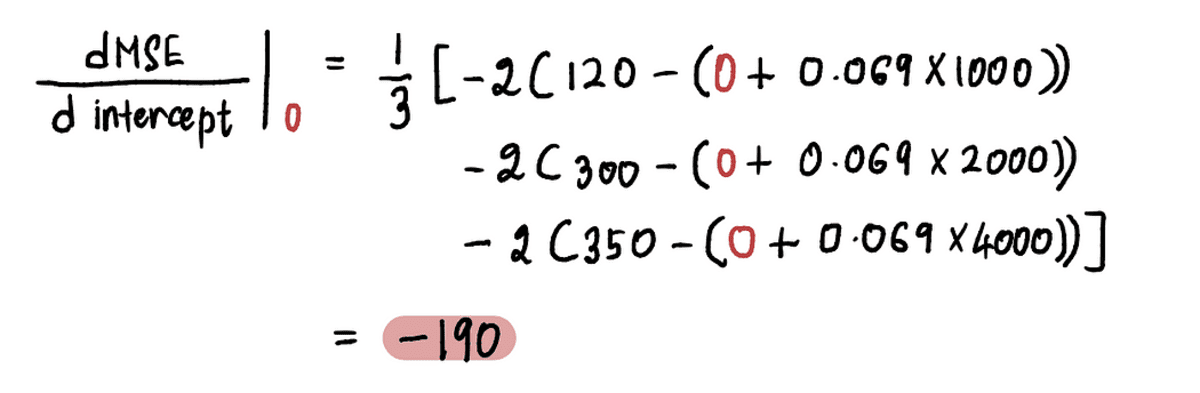
Dus als de onderscheppen = 0, de gradient = -190

NOTITIE: Naarmate we de optimale waarde naderen, naderen de gradiëntwaarden nul. Bij de optimale waarde is de gradiënt gelijk aan nul. Omgekeerd, hoe verder we verwijderd zijn van de optimale waarde, hoe groter de gradiënt wordt.

 

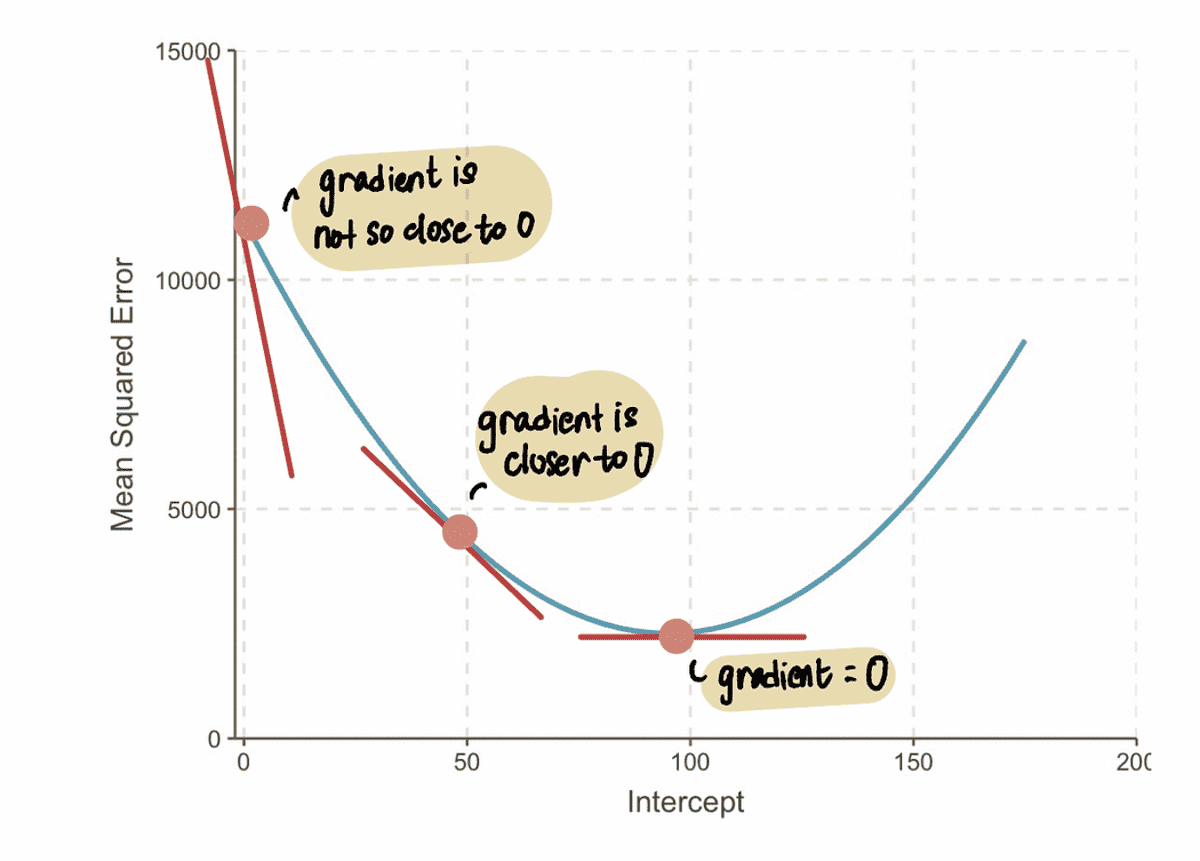
Hieruit kunnen we afleiden dat de stapgrootte gerelateerd moet zijn aan de gradient, omdat het ons vertelt of we een kleine stap of een grote stap moeten zetten. Dit betekent dat wanneer de gradient van de curve dicht bij 0 ligt, dan moeten we kleine stapjes nemen omdat we dicht bij de optimale waarde zitten. En als de gradient groter is, zouden we grotere stappen moeten nemen om sneller tot de optimale waarde te komen.

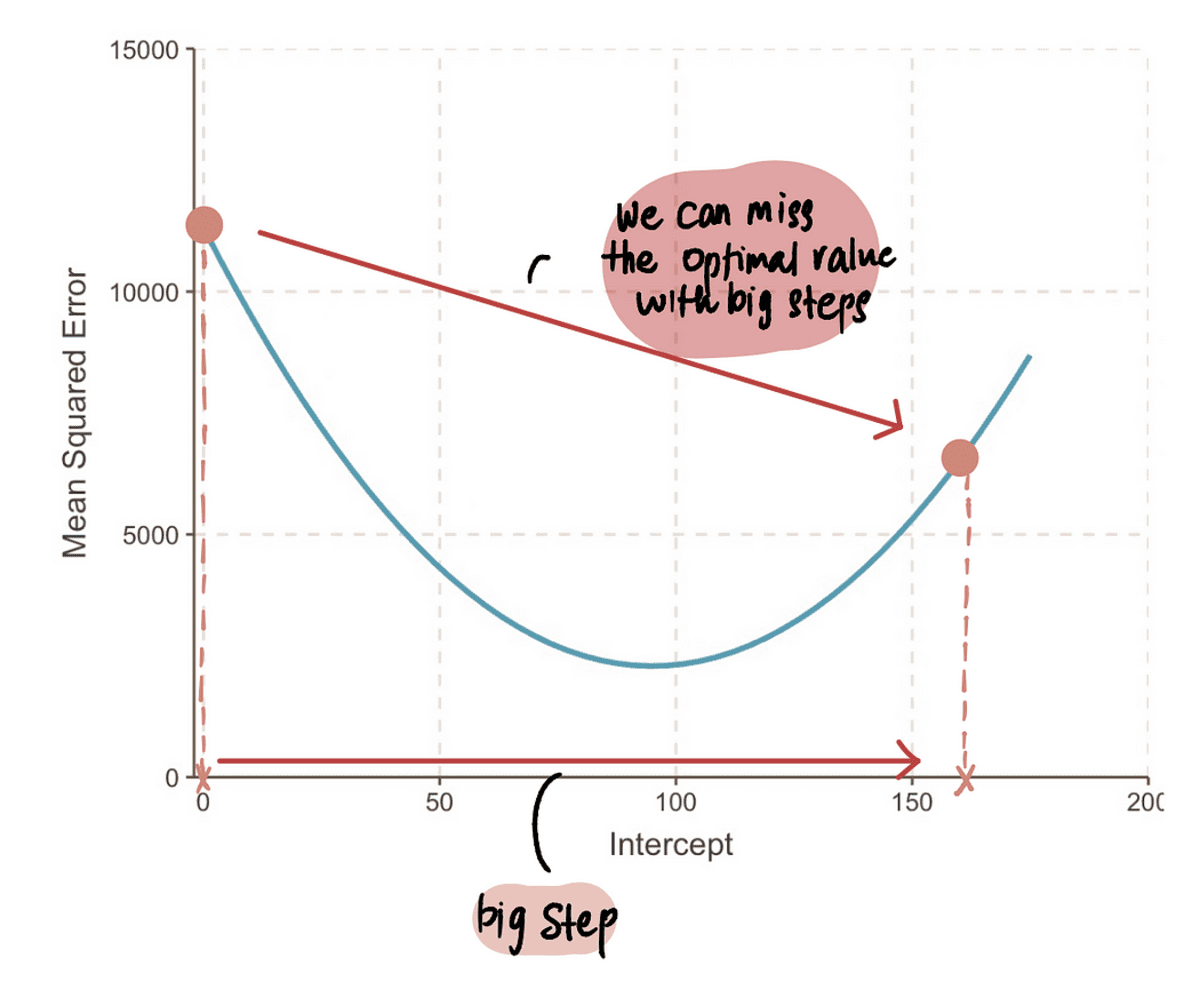
NOTITIE: Als we echter een supergrote stap zetten, kunnen we een grote sprong maken en het optimale punt missen. We moeten dus voorzichtig zijn.

Stap 3: Bereken de stapgrootte met behulp van het verloop en de leersnelheid en werk de onderscheppingswaarde bij

Aangezien we zien dat de Stapgrootte en gradient evenredig aan elkaar zijn, de Stapgrootte wordt bepaald door de te vermenigvuldigen gradient door een vooraf bepaalde constante waarde genaamd de Leertempo:

 

 

De Leren tarief regelt de grootte van de Stapgrootte en zorgt ervoor dat de genomen stap niet te groot of te klein is.

In de praktijk is de leersnelheid meestal een klein positief getal dat ? 0.001. Maar laten we het voor ons probleem instellen op 0.1.

Dus als het snijpunt 0 is, is de Stapgrootte = verloop x Leren tarief = -190*0.1 = -19.

Gebaseerd op de Stapgrootte we hierboven hebben berekend, werken we de onderscheppen (ook wel onze huidige locatie wijzigen) met behulp van een van deze equivalente formules:

 

 

Om het nieuwe te vinden onderscheppen in deze stap voegen we de relevante waarden toe...

 

 

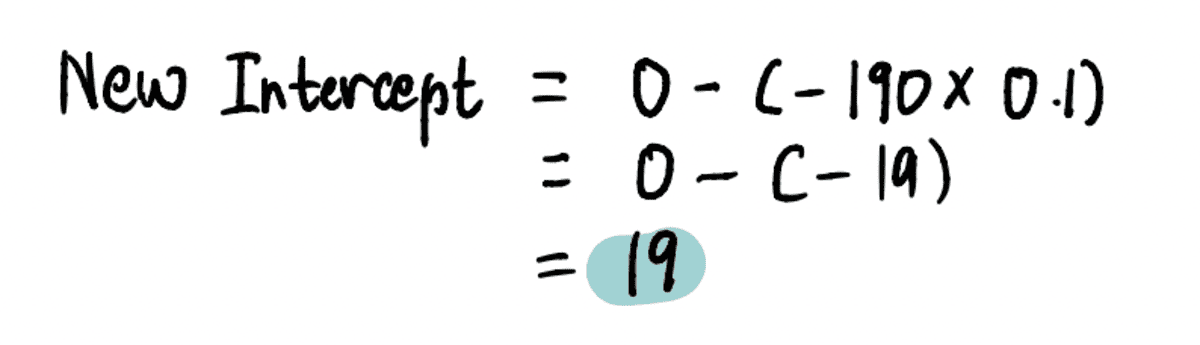
…en vind dat het nieuwe onderscheppen = 19.

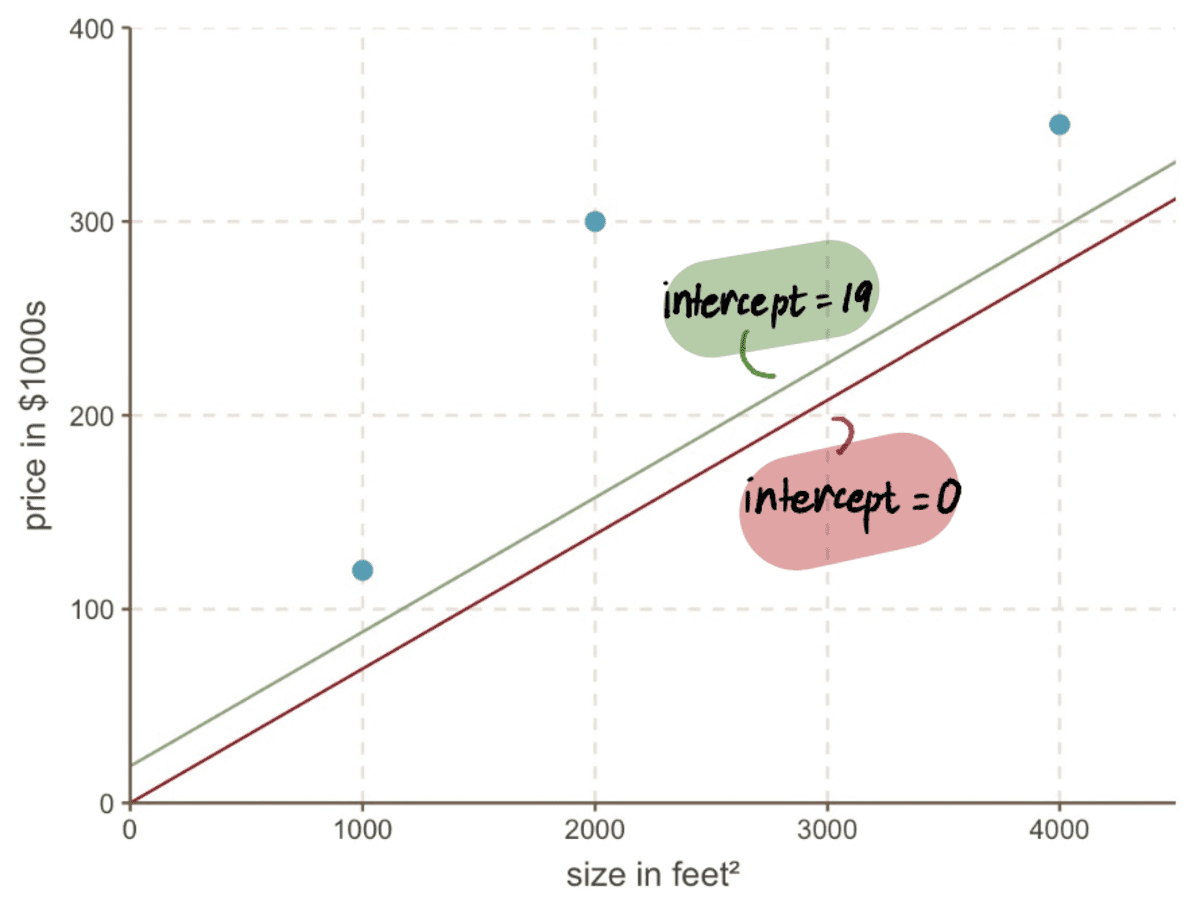
Nu deze waarde inpluggen in de MSE vergelijking vinden we dat de MSE wanneer de onderscheppen is 19 = 8064.095. We merken dat we in één grote stap dichter bij onze optimale waarde zijn gekomen en de MSE.

 

 

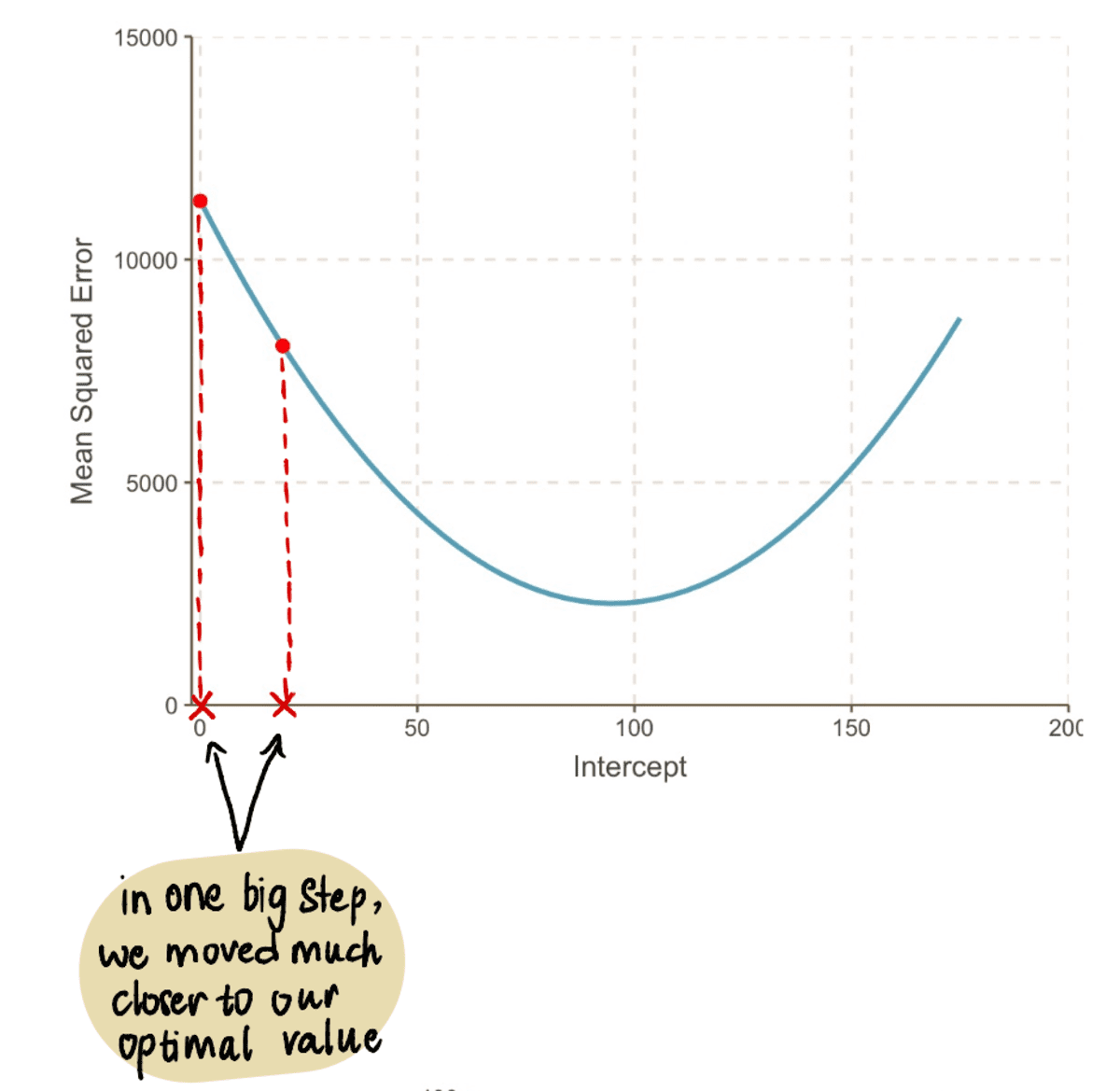
Zelfs als we naar onze grafiek kijken, zien we hoeveel beter onze nieuwe lijn is onderscheppen 19 past onze gegevens dan onze oude lijn aan onderscheppen 0:

 

 

Stap 4: Herhaal stap 2-3

We herhalen stap 2 en 3 met behulp van de bijgewerkte onderscheppen waarde.

Bijvoorbeeld sinds de nieuwe onderscheppen waarde in deze iteratie is 19, volgende Stap 2, zullen we het verloop op dit nieuwe punt berekenen:

 

 

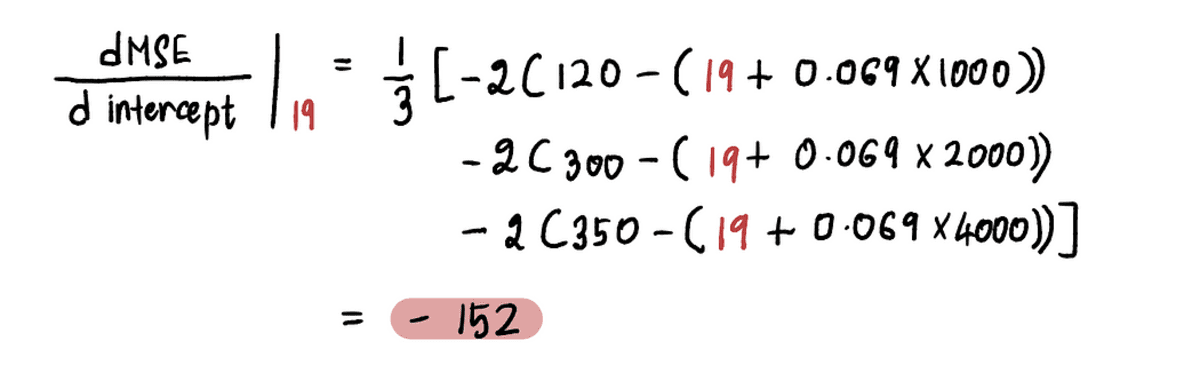
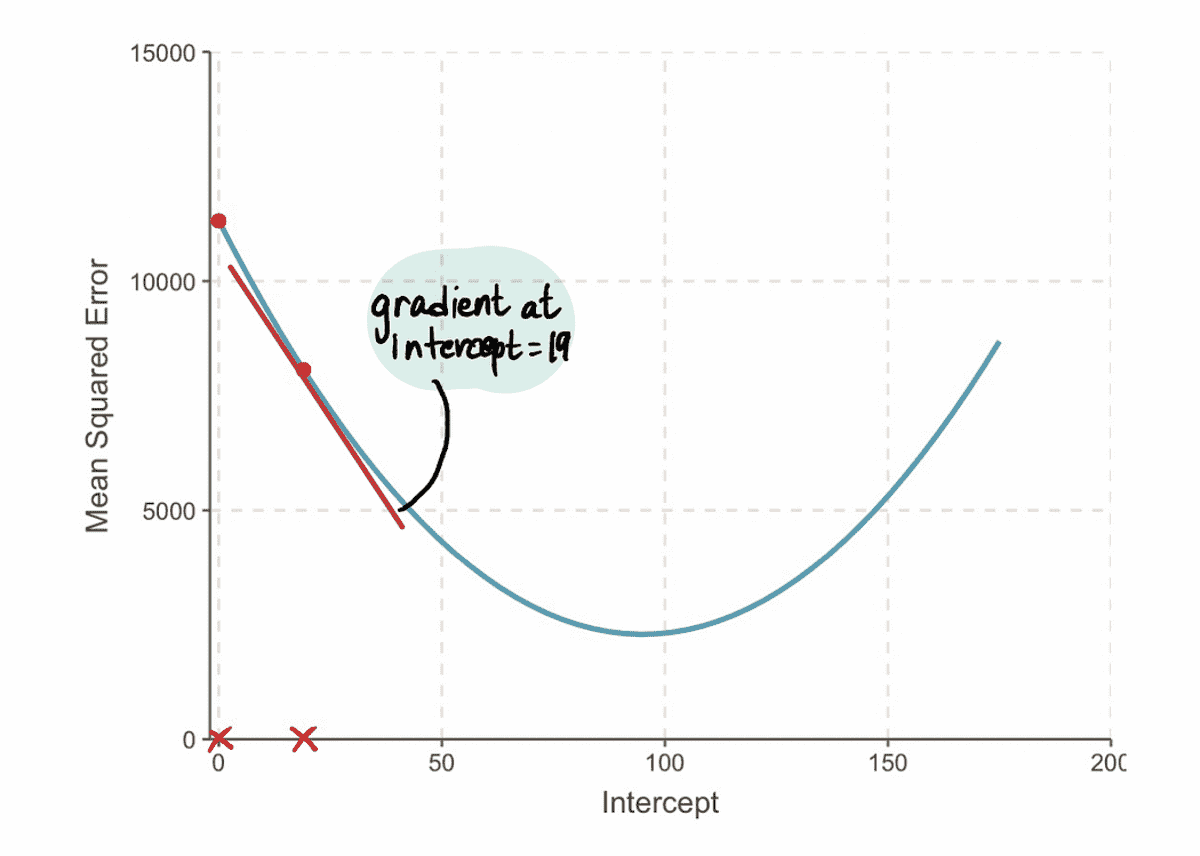
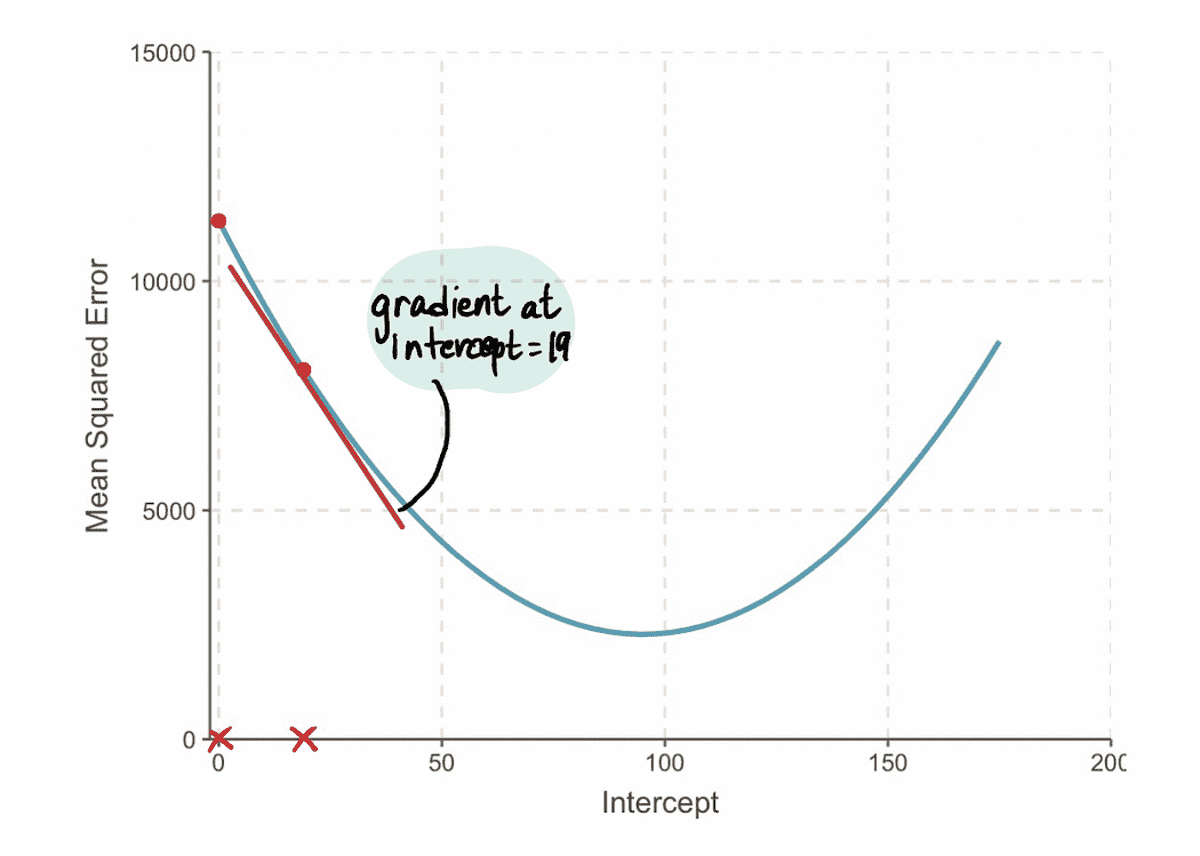
En we vinden dat de gradient van de MSE curve bij de interceptiewaarde van 19 is -152 (zoals weergegeven door de rode raaklijn in de onderstaande afbeelding).

 

 

Vervolgens, in overeenstemming met Stap 3, laten we de berekenen Stapgrootte:

 

 

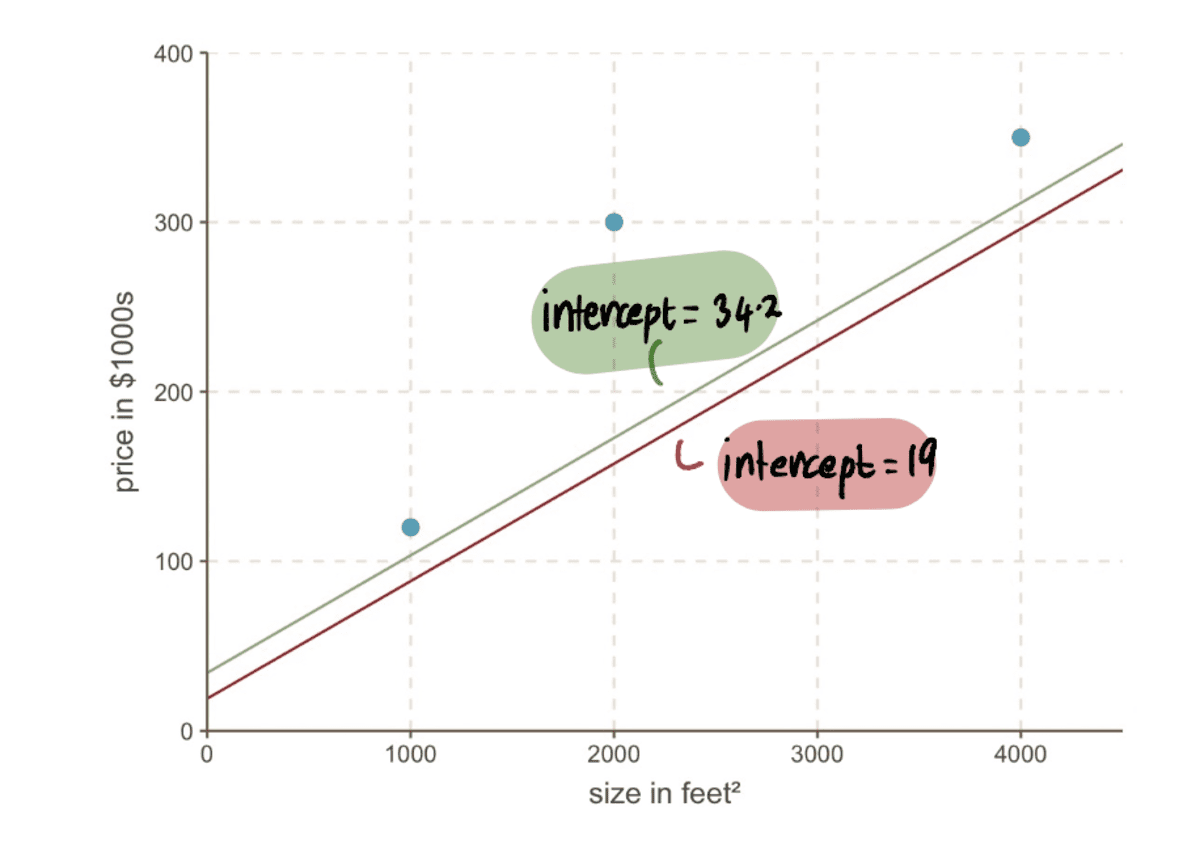
En update vervolgens de onderscheppen waarde:

 

 

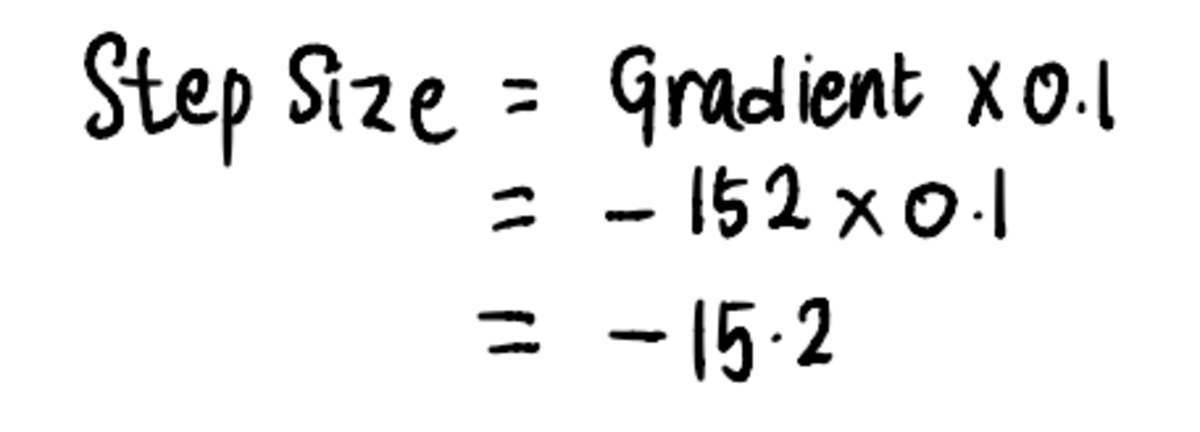
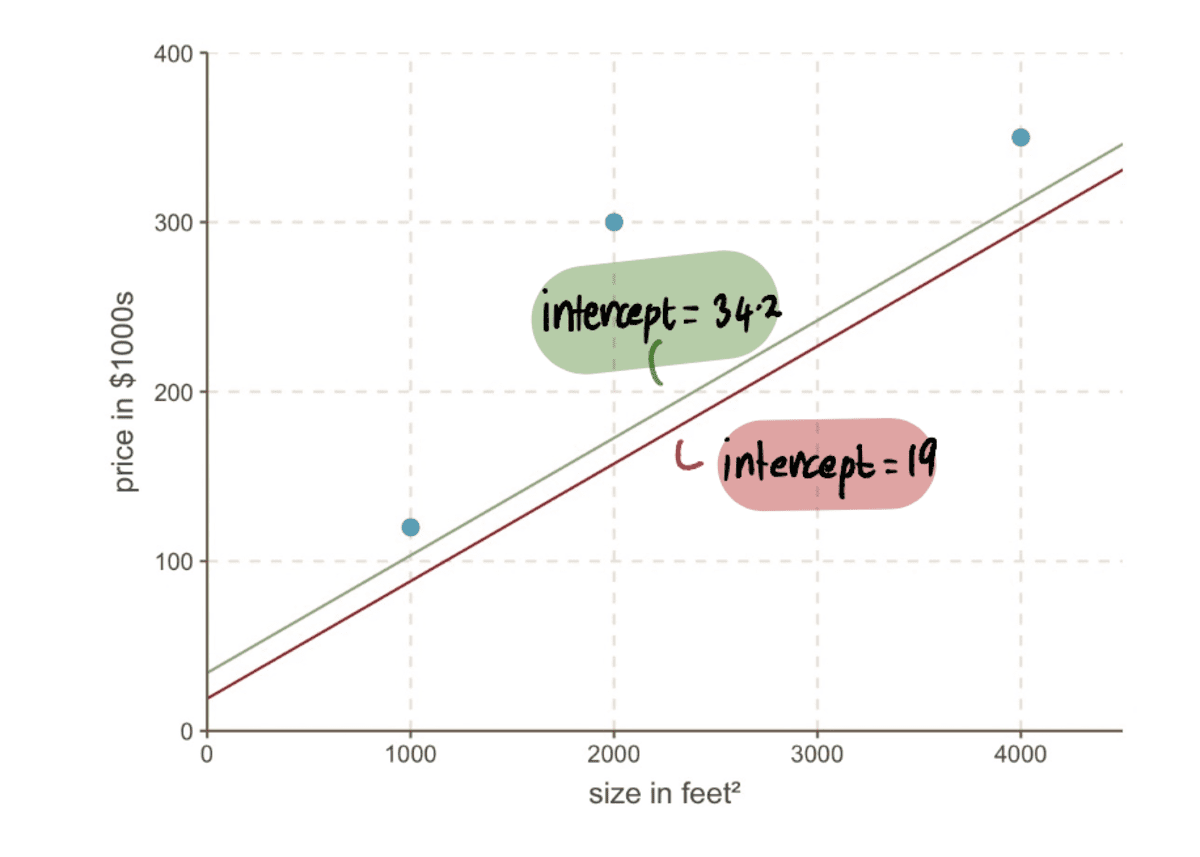
Nu kunnen we de lijn vergelijken met de vorige onderscheppen van 19 naar de nieuwe lijn met het nieuwe intercept 34.2…

 

 

…en we kunnen zien dat de nieuwe regel beter bij de gegevens past.

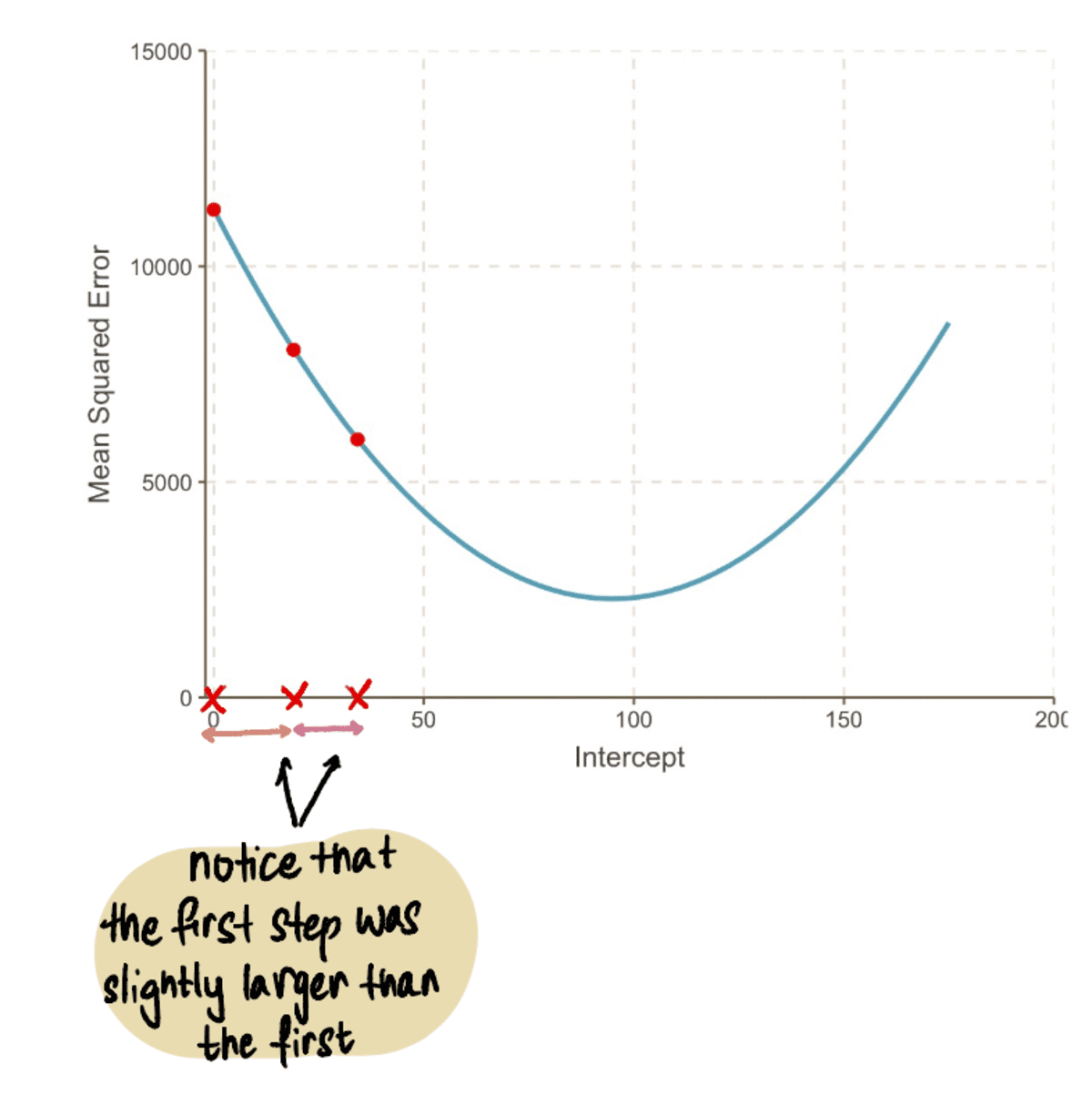
Algemeen, de MSE wordt steeds kleiner...

 

 

…en onze Stapgroottes worden kleiner:

 

 

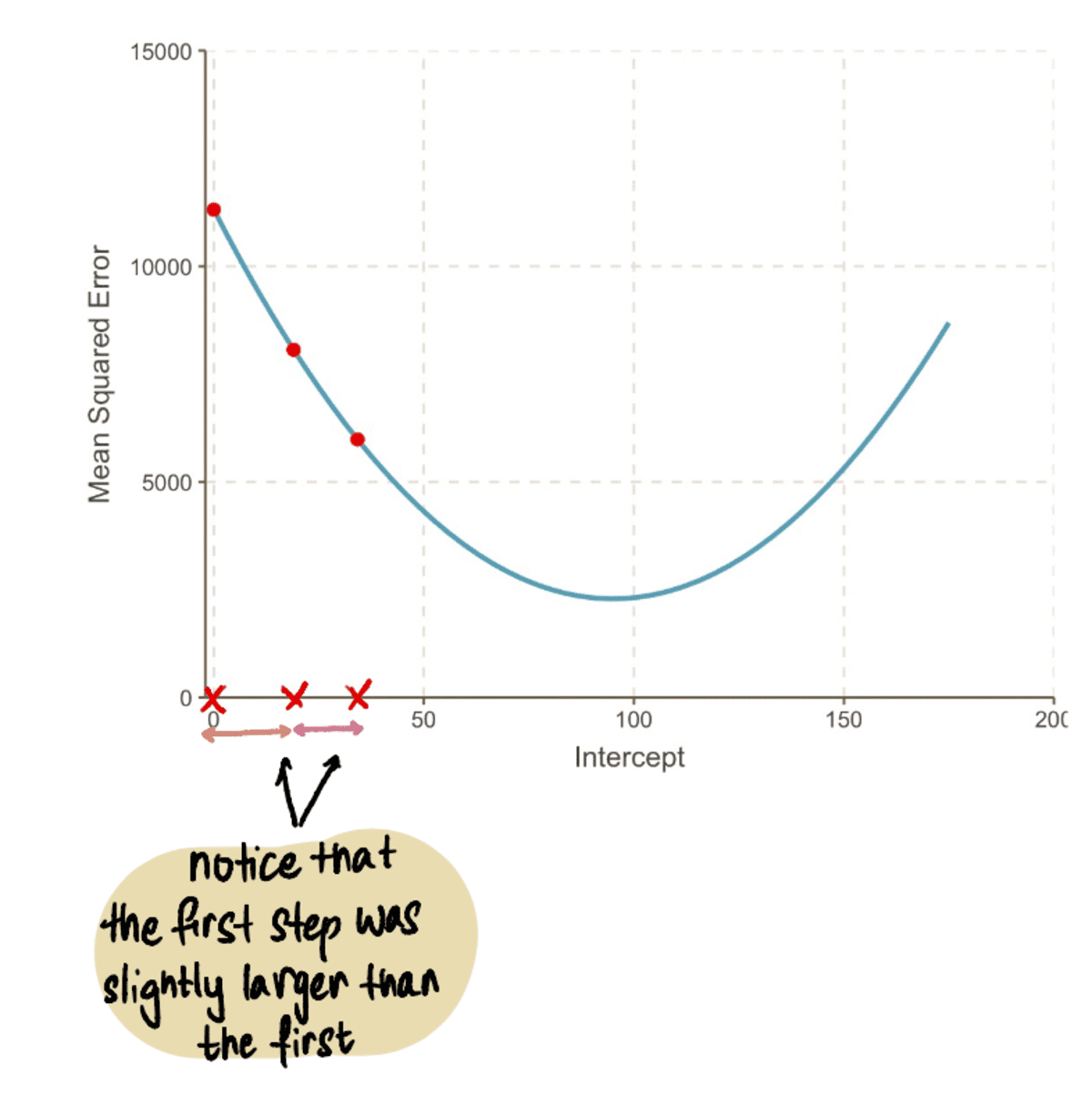
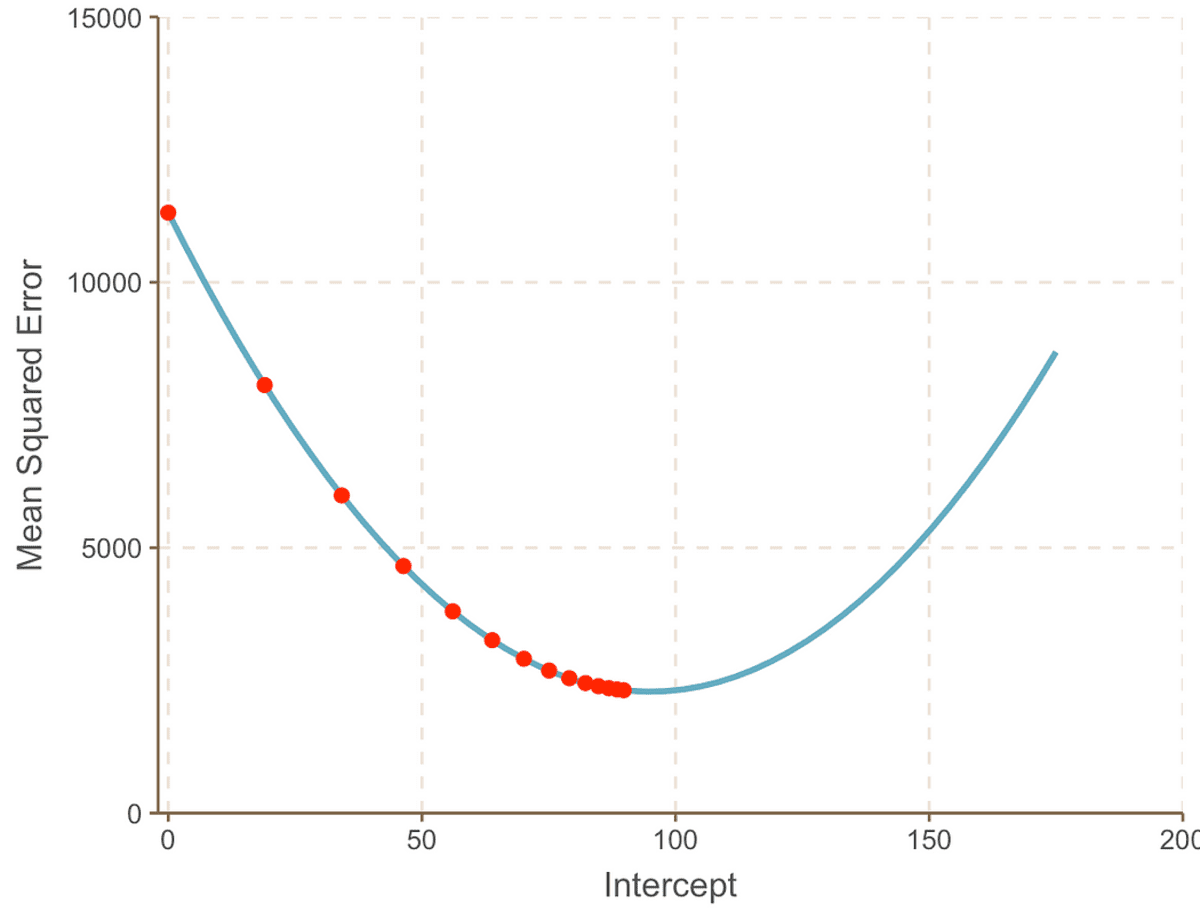
We herhalen dit proces iteratief totdat we convergeren naar de optimale oplossing:

 

 

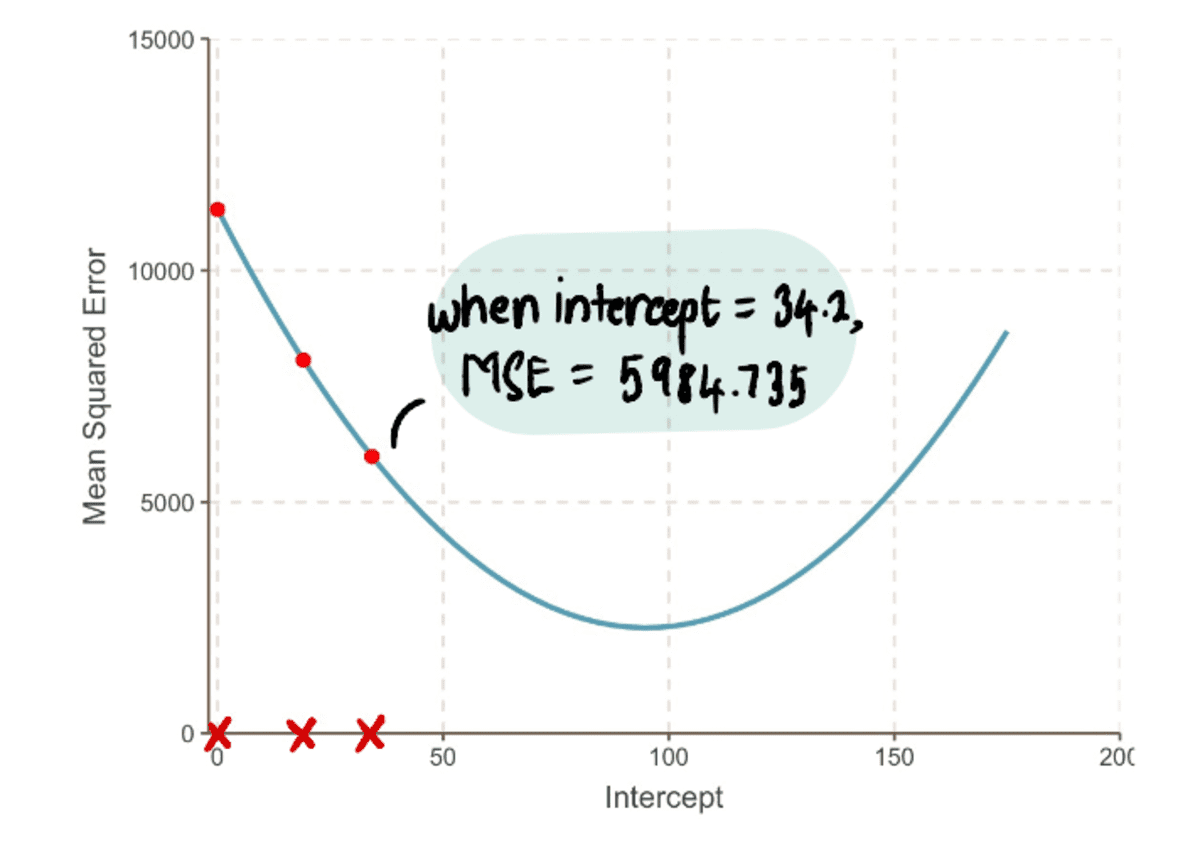
Naarmate we verder gaan naar het minimumpunt van de curve, zien we dat de Stapgrootte wordt steeds kleiner. Na 13 stappen schat het gradiënt-afdalingsalgoritme de onderscheppen waarde op 95. Als we een kristallen bol hadden, zou dit worden bevestigd als het minimumpunt van de MSE kromme. En het is duidelijk om te zien hoe deze methode efficiënter is in vergelijking met de brute force-benadering die we zagen in de vorige artikel.

Nu we de optimale waarde van onze hebben onderscheppen, het lineaire regressiemodel is:

 

 

En de lineaire regressielijn ziet er als volgt uit:

 

best passende lijn met snijpunt = 95 en helling = 0.069

 

Om tot slot terug te komen op de vraag van onze vriend Mark: voor welke waarde moet hij zijn huis van 2400 voet² verkopen?

 

 

Voer de grootte van het huis van 2400 voet² in de bovenstaande vergelijking in ...

 

 

...en voila. We kunnen onze onnodig bezorgde vriend Mark vertellen dat hij op basis van de 3 huizen in zijn buurt zou moeten proberen zijn huis te verkopen voor ongeveer $ 260,600.

Nu we een goed begrip van de concepten hebben, laten we een snelle vraag-en-antwoordsessie houden om eventuele resterende vragen te beantwoorden.

Waarom werkt het vinden van het verloop eigenlijk?

Om dit te illustreren, beschouwen we een scenario waarin we proberen het minimumpunt van curve C te bereiken, aangeduid als x*. En we zijn momenteel bij punt A bij x, gelegen aan de linkerkant van x*:

 

 

Als we de afgeleide nemen van de kromme in punt A ten opzichte van x, vertegenwoordigd als dC(x)/dx, krijgen we een negatieve waarde (dit betekent de gradient helt naar beneden). We merken ook dat we naar rechts moeten bewegen om te bereiken x*. We moeten dus verhogen x om tot het minimum te komen X*.

 

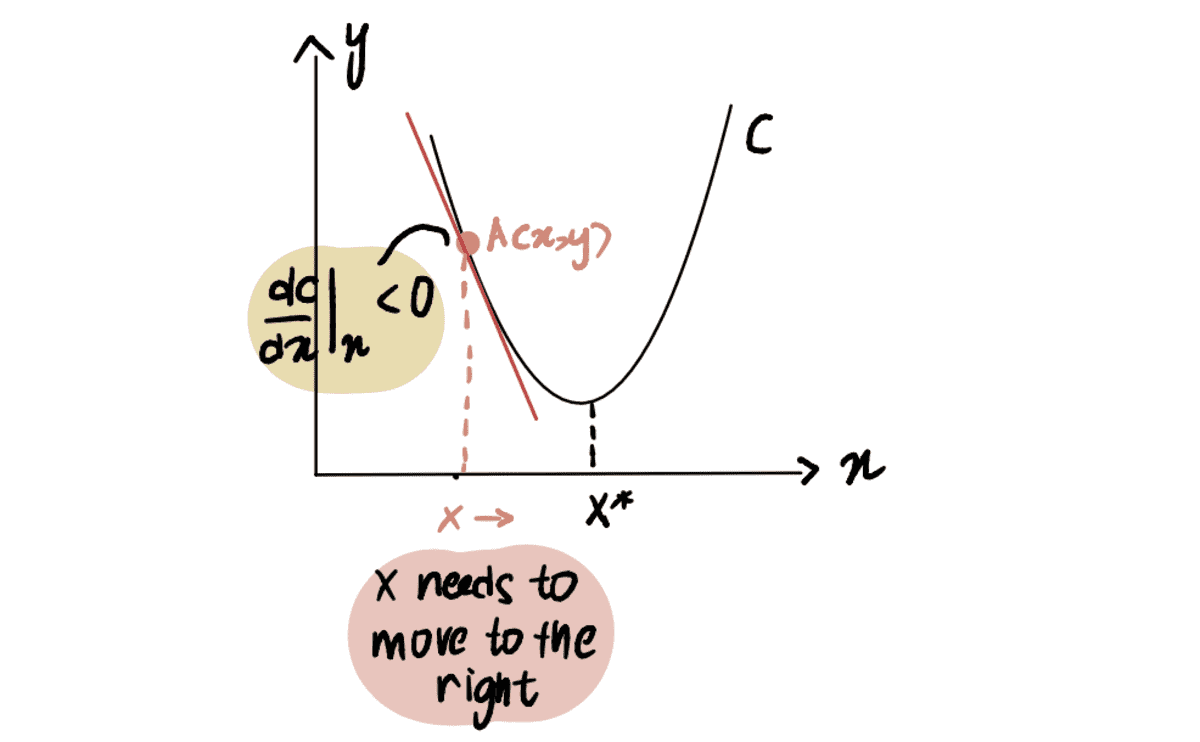
de rode lijn, of het verloop, loopt schuin naar beneden => een negatief verloop

 
 

Sinds dC(x)/dx is negatief, x-??*dC(x)/dx zal groter zijn dan x, dus op weg naar x*.

Evenzo, als we ons in punt A bevinden dat zich rechts van het minimumpunt x* bevindt, krijgen we a positief gradient (gradient loopt schuin omhoog), dC(x)/dx.

 

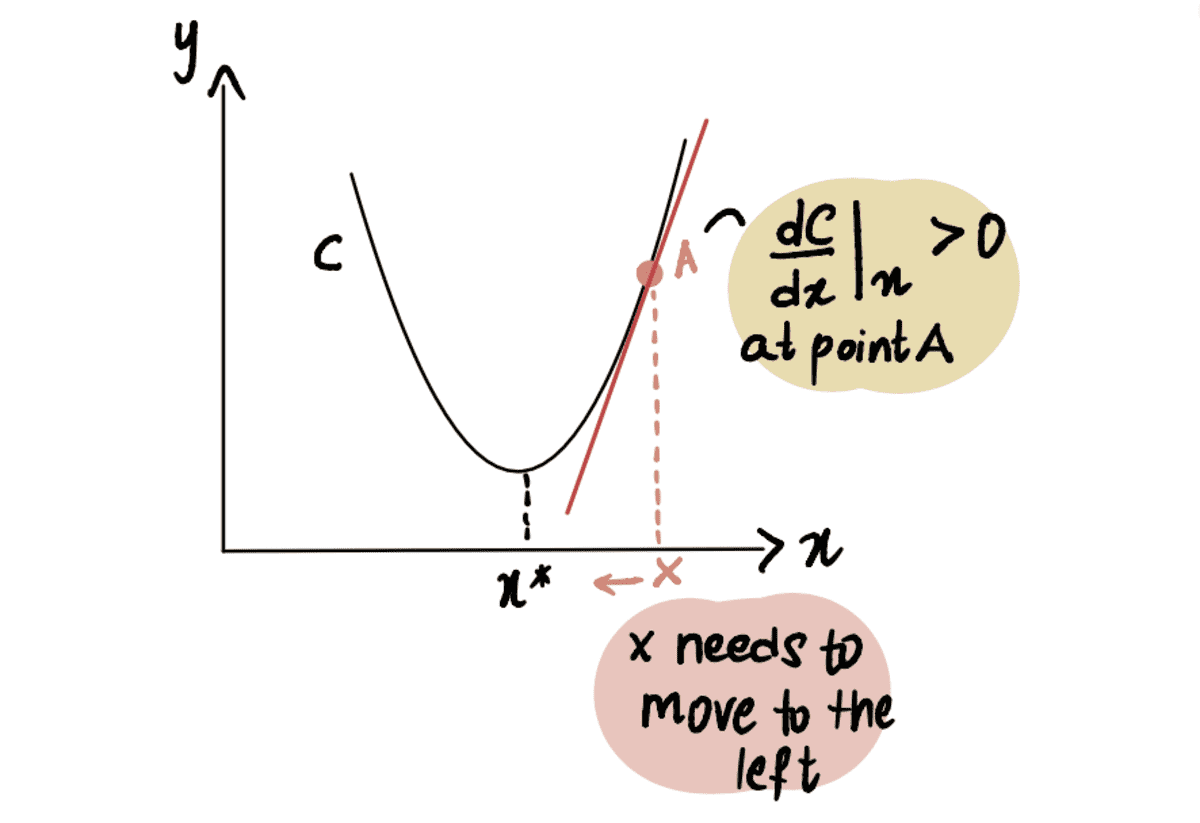
de rode lijn, of het verloop, loopt schuin omhoog => een positief verloop

 

So x-??*dC(x)/dx zal minder zijn dan x, dus op weg naar x*.

Hoe weet Gradiënt fatsoenlijk wanneer hij moet stoppen met het nemen van stappen?

Gradiëntafdaling stopt wanneer de Stapgrootte is zeer dicht bij 0. Zoals eerder besproken, op het minimum punt de gradient is 0 en naarmate we het minimum naderen, wordt de gradient benadert 0. Daarom, wanneer de gradient op een punt ligt dicht bij 0 of in de buurt van het minimumpunt, de Stapgrootte zal ook dicht bij 0 liggen, wat aangeeft dat het algoritme de optimale oplossing heeft bereikt.

 

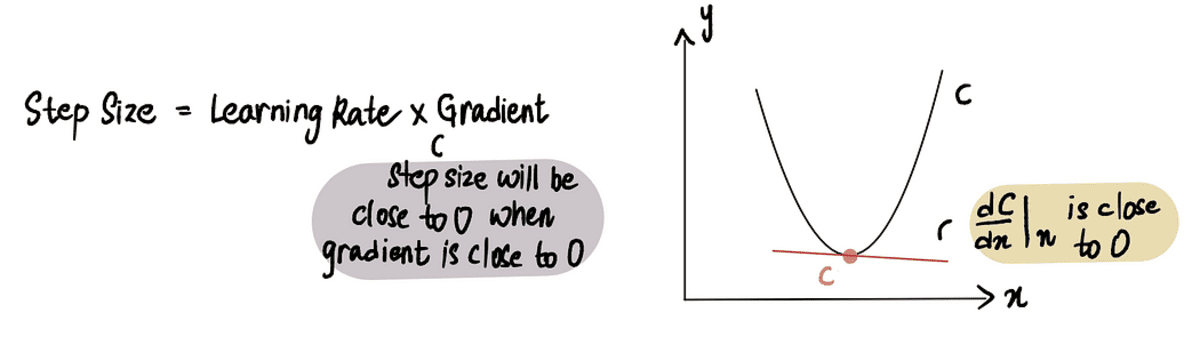
wanneer we dicht bij het minimumpunt zijn, is de gradiënt bijna 0 en vervolgens is de stapgrootte bijna 0

In de praktijk is de minimale stapgrootte = 0.001 of kleiner

 

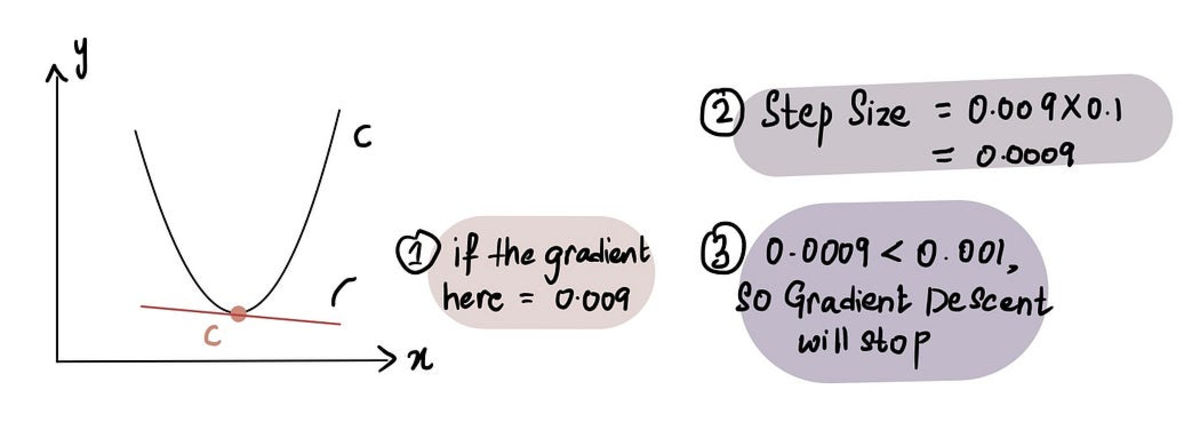
Dat gezegd hebbende, gradiëntafdaling omvat ook een limiet op het aantal stappen dat nodig is voordat het wordt opgegeven, genaamd de Maximaal aantal stappen.

In de praktijk is het maximale aantal stappen = 1000 of meer

Dus zelfs als de Stapgrootte is groter dan de Minimale stapgrootte, als er meer zijn geweest dan de Maximaal aantal stappen, stopt de hellingsafdaling.

Wat als het minimumpunt moeilijker te identificeren is?

Tot nu toe hebben we gewerkt met een curve waarbij het makkelijk is om het minimumpunt te identificeren (dit soort curven worden convex). Maar wat als we een curve hebben die niet zo mooi is (technisch gezien niet-convex) en ziet er zo uit:

 

 

Hier kunnen we zien dat punt B de is globaal minimum (actueel minimum), en punten A en C zijn lokale minima (punten die verward kunnen worden voor de globaal minimum maar niet zijn). Dus als een functie meerdere heeft lokale minima en globaal minimum, is het niet gegarandeerd dat gradiëntafdaling de globaal minimum. Bovendien hangt het lokale minimum dat wordt gevonden af ​​van de positie van de initiële gok (zoals te zien in Stap 1 van gradiëntafdaling).

 

 

Als we deze niet-convexe curve hierboven als voorbeeld nemen, als de initiële gok in Blok A of Blok C is, zal gradiëntafdaling verklaren dat het minimumpunt op lokale minima A of C ligt, terwijl het in werkelijkheid op B is. Alleen als de eerste gok is bij blok B, het algoritme zal het globale minimum B vinden.

Nu is de vraag: hoe maken we een goede eerste gok?

Eenvoudig antwoord: Vallen en opstaan. Soort van.

Niet zo eenvoudig antwoord: Uit de bovenstaande grafiek, als onze minimale schatting van x 0 was aangezien dat in Blok A ligt, zal het leiden tot het lokale minimum A. Dus, zoals je kunt zien, is 0 in de meeste gevallen geen goede eerste gok. Een gangbare praktijk is om een ​​willekeurige functie toe te passen op basis van een uniforme verdeling over het bereik van alle mogelijke waarden van x. Bovendien, indien mogelijk, kan het uitvoeren van het algoritme met verschillende initiële gissingen en het vergelijken van hun resultaten inzicht geven in de vraag of de gissingen significant van elkaar verschillen. Dit helpt om het globale minimum efficiënter te identificeren.

Oké, we zijn er bijna. Laatste vraag.

Wat als we meer dan één optimale waarde proberen te vinden?

Tot nu toe waren we alleen gefocust op het vinden van de optimale onderscheppingswaarde omdat we op magische wijze de helling waarde van de lineaire regressie is 0.069. Maar wat als je geen glazen bol hebt en het optimale niet weet helling waarde? Vervolgens moeten we zowel de hellings- als de onderscheppingswaarden optimaliseren, uitgedrukt als x? en x? respectievelijk.

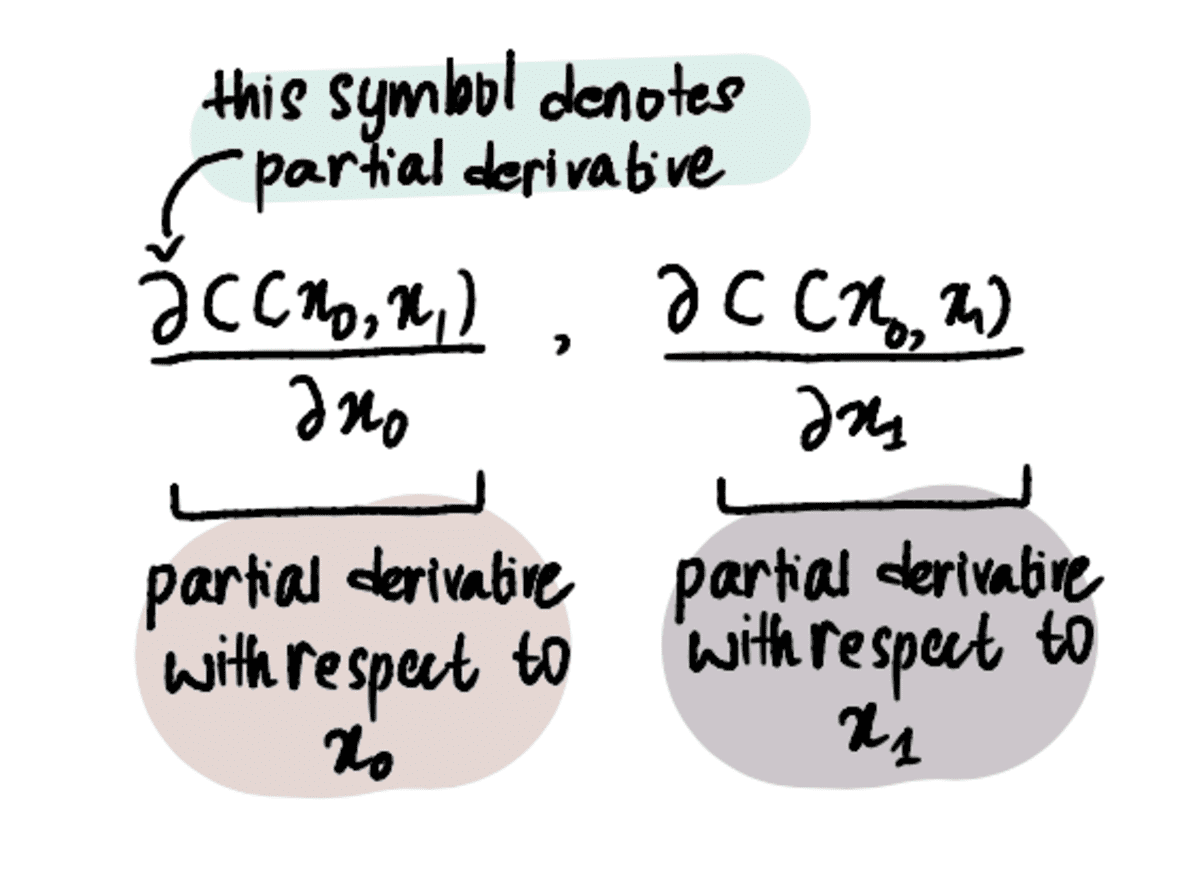
Om dat te doen, moeten we partiële afgeleiden gebruiken in plaats van alleen afgeleiden.

OPMERKING: Gedeeltelijke afgeleiden worden op dezelfde manier berekend als gewone oude afgeleiden, maar worden anders aangeduid omdat we meer dan één variabele hebben waarvoor we proberen te optimaliseren. Lees dit om meer over hen te weten te komen dit artikel of bekijk dit video-.

Het proces blijft echter relatief vergelijkbaar met dat van het optimaliseren van een enkele waarde. De kostenfunctie (bijv MSE) moet nog steeds worden gedefinieerd en het algoritme voor gradiëntafdaling moet worden toegepast, maar met de toegevoegde stap van het vinden van partiële afgeleiden voor beide x? en x?.

Stap 1: Maak eerste schattingen voor x₀ en x₁

Stap 2: Bepaal de partiële afgeleiden naar x₀ en x₁ op deze punten

 

 

Stap 3: Werk x₀ en x₁ gelijktijdig bij op basis van de partiële afgeleiden en de leersnelheid

 

 

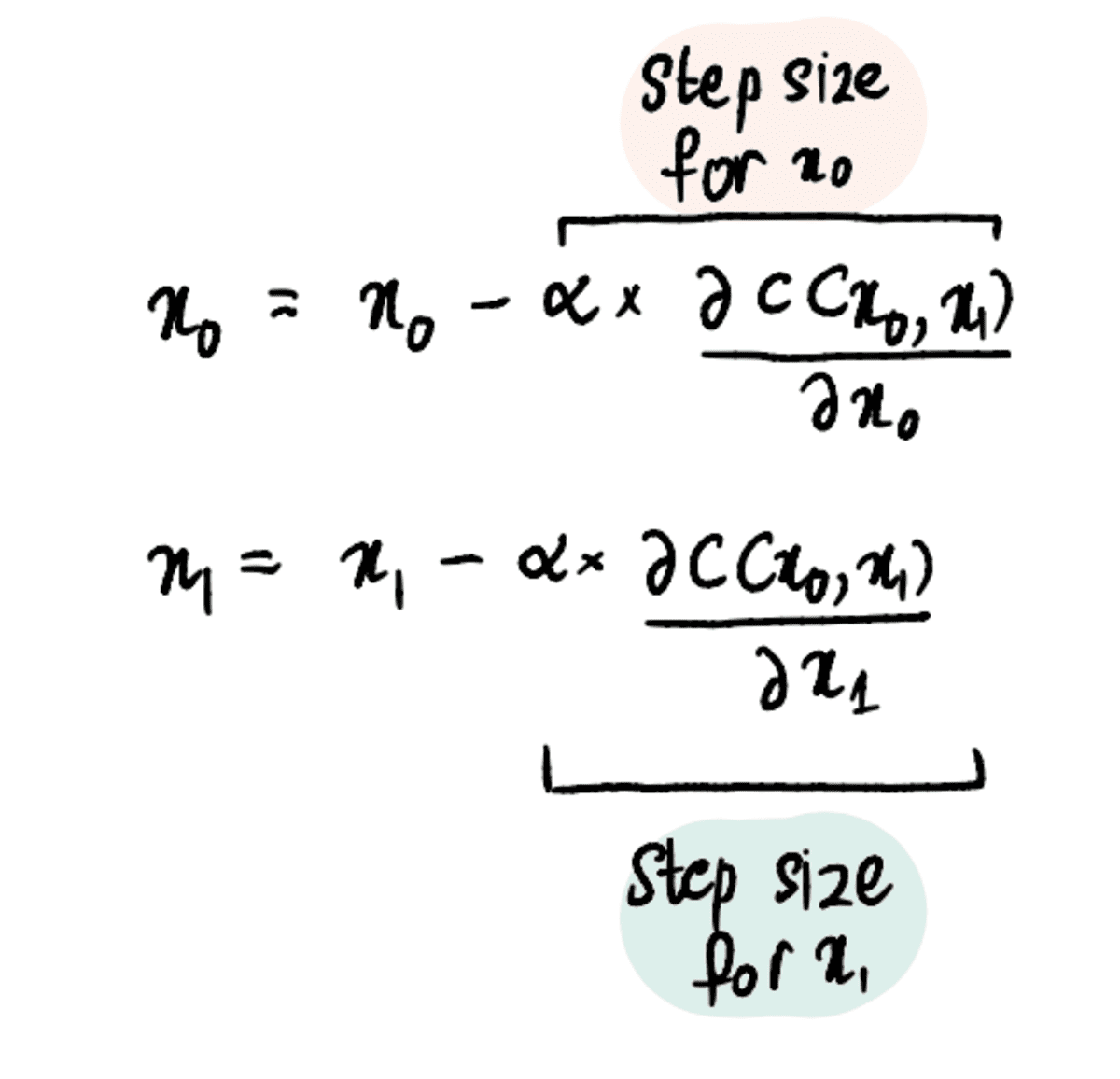
Stap 4: Herhaal stap 2-3 totdat het maximale aantal stappen is bereikt of de stapgrootte kleiner is dan de minimale stapgrootte

En we kunnen deze stappen extrapoleren naar 3, 4 of zelfs 100 waarden om voor te optimaliseren.

Concluderend, gradiëntafdaling is een krachtig optimalisatie-algoritme dat ons helpt de optimale waarde efficiënt te bereiken. Het gradiënt-afdalingsalgoritme kan worden toegepast op veel andere optimalisatieproblemen, waardoor het een fundamenteel hulpmiddel is voor datawetenschappers om in hun arsenaal te hebben. Nu naar grotere en betere algoritmen!

 
 
Shreya Rao illustreren en uitleggen van machine learning-algoritmen in lekentaal.

 
ORIGINELE. Met toestemming opnieuw gepost.
 

• Door SEO aangedreven content en PR-distributie. Word vandaag nog versterkt.
• Platoblockchain. Web3 Metaverse Intelligentie. Kennis versterkt. Toegang hier.
• Bron: https://www.kdnuggets.com/2023/03/back-basics-part-dos-gradient-descent.html?utm_source=rss&utm_medium=rss&utm_campaign=back-to-basics-part-dos-gradient-descent