Ogranicza się do przybliżenia maks. $k$ XOR za pomocą kwantowych i klasycznych algorytmów lokalnych

Opublikowane ponownie przez Plato

Obserwuje: 0

Kunal Marwaha^1,2,3,4 i Stuarta Hadfielda^1,2

¹Laboratorium Kwantowej Sztucznej Inteligencji (QuAIL), Centrum Badawcze NASA Ames, Moffett Field, Kalifornia
²USRA Research Institute for Advanced Computer Science (RIACS), Mountain View, Kalifornia
³Berkeley Centrum Informacji i Obliczeń Kwantowych, Uniwersytet Kalifornijski, Berkeley, Kalifornia
⁴Wydział Informatyki, University of Chicago, Chicago, IL

Czy ten artykuł jest interesujący czy chcesz dyskutować? Napisz lub zostaw komentarz do SciRate.

Abstrakcyjny

Rozważamy moc lokalnych algorytmów dla przybliżonego rozwiązania Max $k$XOR, uogólnienia dwóch problemów spełniania ograniczeń wcześniej badanych za pomocą algorytmów klasycznych i kwantowych (MaxCut i Max E3LIN2). W Max $k$XOR każde ograniczenie jest XOR dokładnie $k$ zmiennych i bitem parzystości. W przypadkach ze znakami losowymi (parzystościami) lub bez nakładających się klauzul i klauzulami $D+1$ na zmienną, obliczamy oczekiwany satysfakcjonujący ułamek QAOA głębokości-1 z Farhi i in. [arXiv:1411.4028] i porównujemy z uogólnieniem algorytm lokalnego progu z Hirvonen i wsp. [arXiv:1402.2543]. Warto zauważyć, że algorytm kwantowy przewyższa algorytm progowy dla $k$$gt$$4$.

Z drugiej strony zwracamy uwagę na potencjalne trudności dla QAOA w osiągnięciu obliczeniowej przewagi kwantowej w tym problemie. Najpierw obliczamy ścisłe górne ograniczenie dla maksymalnego satysfakcjonującego ułamka prawie wszystkich dużych przypadkowych regularnych instancji Max $k$XOR, obliczając numerycznie gęstość energii stanu podstawowego $P(k)$ średniego pola $k$-spinowego szkła [ arXiv:1606.02365]. Górna granica rośnie z $k$ znacznie szybciej niż wydajność obu algorytmów jednolokalnych. Identyfikujemy również nowy wynik obstrukcji dla obwodów kwantowych o małej głębokości (w tym QAOA), gdy $k=3$, uogólniając wynik Bravyi i in. [arXiv:1910.08980], gdy $k=2$. Przypuszczamy, że podobna przeszkoda istnieje dla wszystkich $k$.

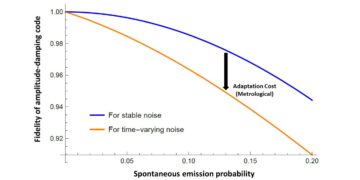
Wyróżniony obraz: Porównanie zadowalającego ułamka (wydajności) algorytmu progowego i głębokości-1 QAOA dla Max kXOR przy dużym $D$ (i $D gg k$). Stała $C_k$ dla QAOA rośnie szybciej z $k$ niż dla algorytmu progowego. Chociaż algorytm progowy przewyższa QAOA głębokości-1 dla $k w {2,3,4}$, przy wszystkich innych k, QAOA jest lepszym algorytmem.

[Osadzone treści]

► Dane BibTeX

@artykuł{Marwaha2022graniceprzybliżone, doi = {10.22331/q-2022-07-07-757}, url = {https://doi.org/10.22331/q-2022-07-07-757}, title = {Granice aproksymacji {M}ax {$k$}{XOR} kwantowymi i klasycznymi algorytmami lokalnymi}, autor = {Marwaha, Kunal i Hadfield, Stuart}, czasopismo = {{Quantum}}, issn = {2521-327X}, wydawca = {{Verein zur F{“{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}}, objętość = {6}, strony = {757}, miesiąc = lipiec, rok = {2022} }

► Referencje

[1] A. Auffinger i W.-K. Chen. O własnościach miar paryskich. arXiv:1303.3573, doi:10.1007/s00440-014-0563-y.
https: / / doi.org/ 10.1007 / s00440-014-0563-y
arXiv: 1303.3573

[2] A. Auffinger i W.-K. Chen. Formuła Parisi posiada unikalny minimalizator. Communications in Mathematical Physics, 335(3):1429–1444, listopad 2014. arXiv:1402.5132, doi:10.1007/s00220-014-2254-z.
https: / / doi.org/ 10.1007 / s00220-014-2254-z
arXiv: 1402.5132

[3] A. Auffinger i W.-K. Chen. Wzór Parisiego na energię stanu podstawowego w mieszanym modelu p-spinowym. arXiv:1606.05335, doi:10.1214/16-aop1173.
https:///doi.org/10.1214/16-aop1173
arXiv: 1606.05335

[4] AE Alaoui i A. Montanari. Progi algorytmiczne w średniopolowych szkłach wirowych. arXiv:2009.11481.
arXiv: 2009.11481

[5] AE Alaoui, A. Montanari i M. Sellke. Optymalizacja szkieł spinowych średniego pola. arXiv:2001.00904, doi:10.1214/21-aop1519.
https:///doi.org/10.1214/21-aop1519
arXiv: 2001.00904

[6] S. Bravyi, A. Kliesch, R. Koenig i E. Tang. Przeszkody w przygotowaniu stanu i optymalizacji wariacyjnej ochrony symetrii. Preprint arXiv, 2019. arXiv:1910.08980.
https: / / doi.org/ 10.1103 / PhysRevLett.125.260505
arXiv: 1910.08980

[7] B. Barak i K. Marwaha. Klasyczne algorytmy i ograniczenia kwantowe dla maksymalnego cięcia na grafach o dużym obwodzie. arXiv:2106.05900, doi:10.4230/LIPics.ITCS.2022.14.
https: / / doi.org/ 10.4230 / LIPIcs.ITCS.2022.14
arXiv: 2106.05900

[8] B. Barak, A. Moitra, R. O'Donnell, et al. Pokonanie losowego przypisania na problemach spełniania ograniczeń o ograniczonym stopniu. arXiv:1505.03424.
arXiv: 1505.03424

[9] W.-K. Chen, D. Gamarnik, D. Panchenko i M. Rahman. Suboptymalność algorytmów lokalnych dla klasy problemów z maksymalnym cięciem. The Annals of Probability, 47(3), maj 2019. arXiv:1707.05386, doi:10.1214/18-aop1291.
https:///doi.org/10.1214/18-aop1291
arXiv: 1707.05386

[10] C.-N. Chou, PJ Love, JS Sandhu i J. Shi. Ograniczenia lokalnych algorytmów kwantowych na losowym Max-k-XOR i poza nim. arXiv:2108.06049.
arXiv: 2108.06049

[11] A. Crisanti i T. Rizzo. Analiza rozwiązania łamania symetrii $infty$-repliki modelu Sherringtona-Kirkpatricka. Physical Review E, 65(4), kwiecień 2002. arXiv:cond-mat/0111037, doi:10.1103/physreve.65.046137.
https: / / doi.org/ 10.1103 / physreve.65.046137
arXiv: cond-mat / 0111037

[12] B. Derridę. Model energii losowej: dokładnie rozwiązywalny model układów nieuporządkowanych. Fiz. Rev B, 24:2613–2626, wrzesień 1981. doi:10.1103/PhysRevB.24.2613.
https: / / doi.org/ 10.1103 / PhysRevB.24.2613

[13] A. Dembo, A. Montanari i S. Sen. Ekstremalne cięcia rzadkich wykresów losowych. The Annals of Probability, 45(2):1190–1217, 2017. arXiv:1503.03923, doi:10.1214/15-aop1084.
https:///doi.org/10.1214/15-aop1084
arXiv: 1503.03923

[14] L. Eldara i AW Harrowa. Lokalni hamiltonianie, których stany podstawowe są trudne do przybliżenia. 2017 IEEE 58th Annual Symposium on Foundations of Computer Science (FOCS), październik 2017. arXiv:1510.02082, doi:10.1109/focs.2017.46.
https: / / doi.org/ 10.1109 / focs.2017.46
arXiv: 1510.02082

[15] E. Farhi, J. Goldstone i S. Gutmann. Algorytm optymalizacji kwantowej aproksymowanej. arXiv:1411.4028.
arXiv: 1411.4028

[16] E. Farhi, J. Goldstone i S. Gutmann. Algorytm aproksymacji kwantowej zastosowany do problemu z ograniczeniem występowania ograniczonego występowania. arXiv: 1412.6062.
arXiv: 1412.6062

[17] E. Farhi, D. Gamarnik i S. Gutmann. Algorytm optymalizacji kwantowej aproksymowanej musi widzieć cały wykres: Typowy przypadek. arXiv:2004.09002.
arXiv: 2004.09002

[18] J. Friedmana. Dowód drugiej hipotezy Alona o wartości własnej i związanych z nią problemów. arXiv:cs/0405020, doi:10.1090/memo/0910.
https:///doi.org/10.1090/memo/0910
arXiv: cs / 0405020

[19] S. Hadfielda. Algorytmy kwantowe do obliczeń naukowych i przybliżonej optymalizacji. Uniwersytet Columbia, 2018, arXiv:1805.03265.
arXiv: 1805.03265

[20] J. Håstada. Niektóre optymalne wyniki nieprzybliżeniowości. Journal of the ACM (JACM), 48(4):798–859, 2001. doi:10.1145/258533.258536, URL http://www.cs.umd.edu/ gasarch/BLOGPAPERS/max3satl. pdf.
https: / / doi.org/ 10.1145 / 258533.258536
http:///www.cs.umd.edu/~gasarch/BLOGPAPERS/max3satl.pdf

[21] MB Hastings. Trywialne stany niskoenergetyczne dla hamiltonianów dojazdowych i hipoteza kwantowego PCP. Informacje i obliczenia kwantowe, 13, 2013. arXiv:1201.3387, doi:10.26421/qic13.5-6-3.
https: / / doi.org/ 10.26421 / qic13.5-6-3
arXiv: 1201.3387

[22] MB Hastings. Klasyczne i kwantowe algorytmy aproksymacji głębi. arXiv:1905.07047, doi:10.26421/qic19.13-14-3.
https: / / doi.org/ 10.26421 / qic19.13-14-3
arXiv: 1905.07047

[23] WW Ho i TH Hsieh. Efektywna symulacja wariacyjna nietrywialnych stanów kwantowych. arXiv:1803.00026, doi:10.21468/scipostphys.6.3.029.
https: / / doi.org/ 10.21468 / scipostphys.6.3.029
arXiv: 1803.00026

[24] J. Hirvonen, J. Rybicki, S. Schmid, J. Suomela. Duże cięcia z lokalnymi algorytmami na grafach bez trójkątów. The Electronic Journal of Combinatorics, strony P4–21, 2017. arXiv:1402.2543, doi:10.37236/6862.
https: / / doi.org/ 10.37236 / 6862
arXiv: 1402.2543

[25] CY-Y. Lin i Y. Zhu. Wykonanie QAOA na typowych przypadkach problemów ze spełnieniem ograniczeń o ograniczonym stopniu. arXiv:1601.01744.
arXiv: 1601.01744

[26] K. Marwaha. Lokalny klasyczny algorytm MAX-CUT przewyższa $p=2$ QAOA na grafach regularnych o dużym obwodzie. Quantum, 5:437, kwiecień 2021. arXiv:2101.05513, doi:10.22331/q-2021-04-20-437.
https://doi.org/10.22331/q-2021-04-20-437
arXiv: 2101.05513

[27] A. Montanari. Optymalizacja hamiltonianu Sherringtona-Kirkpatricka. arXiv:1812.10897, doi:10.1109/focs.2019.00087.
https: / / doi.org/ 10.1109 / focs.2019.00087
arXiv: 1812.10897

[28] P. Obszarski i A. Jastrzębski. Kolorowanie krawędzi hipergrafów 3-jednorodnych. Discrete Applied Mathematics, 217: 48–52, 2017, Optymalizacja kombinatoryczna: teoria, obliczenia i zastosowania. doi:10.1016/j.dam.2016.06.009.
https: // doi.org/ 10.1016 / j.dam.2016.06.009

[29] D. Panchenko. Wprowadzenie do modelu SK. arXiv:1412.0170, doi:10.4310/cdm.2014.v2014.n1.a4.
https://doi.org/10.4310/cdm.2014.v2014.n1.a4
arXiv: 1412.0170

[30] D. Panchenko. W modelu $k$-sat z dużą liczbą klauzul. arXiv:1608.06256, doi:10.1002/rsa.20748.
https: // doi.org/ 10.1002 / rsa.20748
arXiv: 1608.06256

[31] G. Parisi. Sekwencja przybliżonych rozwiązań modelu SK dla szkieł spinowych. Journal of Physics A: Mathematical and General, 13(4):L115–L121, kwiecień 1980. doi:10.1088/0305-4470/13/4/009.
https://doi.org/10.1088/0305-4470/13/4/009

[32] S. Sen. Optymalizacja na nielicznych hipergrafach losowych i szkłach spinowych. arXiv:1606.02365, doi:10.1002/rsa.20774.
https: // doi.org/ 10.1002 / rsa.20774
arXiv: 1606.02365

[33] R. Shaydulin, S. Hadfield, T. Hogg i I. Safro. Symetrie klasyczne i algorytm aproksymacji kwantowej. Kwantowe przetwarzanie informacji, 20(11):1–28, 2021. arXiv:2012.04713, doi:10.1007/s11128-021-03298-4.
https://doi.org/10.1007/s11128-021-03298-4
arXiv: 2012.04713

[34] Pan Talagrand. Formuła paryska. Annals of Mathematics, 163:221–263, 2006. doi:10.4007/annals.2006.163.221, URL https:///annals.math.princeton.edu/wp-content/uploads/annals-v163 -n1-p04.pdf.
https: // doi.org/ 10.4007 / annals.2006.163.221
https:///annals.math.princeton.edu/wp-content/uploads/annals-v163-n1-p04.pdf

[35] Z. Wang, S. Hadfield, Z. Jiang i EG Rieffel. Algorytm aproksymacji kwantowej dla maxcut: Widok fermionowy. Fiz. Rev. A, 97:022304, luty 2018. arXiv:1706.02998, doi:10.1103/PhysRevA.97.022304.
https: / / doi.org/ 10.1103 / PhysRevA.97.022304
arXiv: 1706.02998

Cytowany przez

[1] Joao Basso, Edward Farhi, Kunal Marwaha, Benjamin Villalonga i Leo Zhou, „Algorytm optymalizacji kwantowej na dużej głębokości dla MaxCut na wykresach regularnych o dużym obwodzie i modelu Sherringtona-Kirkpatricka”, arXiv: 2110.14206.

[2] Nicolas PD Sawaya, Albert T Schmitz i Stuart Hadfield, „Kodowanie kompromisów i zestawów narzędzi projektowych w algorytmach kwantowych do optymalizacji dyskretnej: kolorowanie, trasowanie, planowanie i inne problemy”, arXiv: 2203.14432.

[3] Yash J. Patel, Sofiene Jerbi, Thomas Bäck i Vedran Dunjko, „Reinforcement Learning Assisted Recursive QAOA”, arXiv: 2207.06294.

Powyższe cytaty pochodzą z Reklamy SAO / NASA (ostatnia aktualizacja pomyślnie 2022-07-26 13:36:03). Lista może być niekompletna, ponieważ nie wszyscy wydawcy podają odpowiednie i pełne dane cytowania.

On Serwis cytowany przez Crossref nie znaleziono danych na temat cytowania prac (ostatnia próba 2022-07-26 13:36:00).

Niniejszy artykuł opublikowano w Quantum pod Creative Commons Uznanie autorstwa 4.0 Międzynarodowe (CC BY 4.0) licencja. Prawa autorskie należą do pierwotnych właścicieli praw autorskich, takich jak autorzy lub ich instytucje.