Kwantowa teoria pola podważa otwartą zagadkę matematyczną

W zeszłym miesiącu, Karen Vogtmann i Michał Boryński opublikował dowód że w niedostępnym dotąd świecie matematycznym, zwanym przestrzenią modułów grafów, znajduje się ciężarówka struktur matematycznych, którą Vogtmann i współpracownik pierwszy opisany w połowie 1980-ów.

„To bardzo trudny problem. To niesamowite, że byli w stanie” – powiedział Dan Margalit, matematyk z Georgia Institute of Technology.

Vogtmann i Borinsky zaczęli od pytań, które Vogtmann, matematyk z University of Warwick, zadawała sobie przez dziesięciolecia. Następnie para ponownie przedstawiła problem w języku fizyki, używając technik z kwantowej teorii pola, aby uzyskać wynik.

Dowód pokazuje, że w przestrzeni modułów istnieją pewne struktury, ale nie ujawnia wprost, jakie to są struktury. W ten sposób ich nowy wynik bardziej przypomina wykrywacz metalu niż kamerę — ostrzega ich, że kryje się coś interesującego, mimo że nie potrafią tego w pełni opisać.

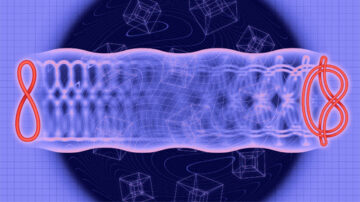
Możesz myśleć o przestrzeniach modułów grafów jako o kształtach matematycznych z dodaną dekoracją. Jeśli staniesz w dowolnym punkcie kształtu, zobaczysz unoszący się nad tobą wykres — zbiór punktów lub wierzchołków połączonych krawędziami. W różnych miejscach na przestrzeni modułów grafy zmieniają się, ich krawędzie kurczą się lub rosną, a czasami całkowicie znikają. Ze względu na te cechy Borinsky, fizyk matematyczny ze Szwajcarskiego Federalnego Instytutu Technologii w Zurychu, opisuje przestrzenie modułów jako „wielkie morze grafów”.

„Ranga” wykresu to liczba jego pętli; dla każdego rzędu grafów istnieje przestrzeń modułów. Rozmiar tej przestrzeni szybko rośnie — jeśli ustalisz długości krawędzi wykresu, pojawią się trzy wykresy o randze 2, 15 o randze 3, 111 o randze 4 i 2,314,204,852 10 XNUMX XNUMX o randze XNUMX. W przestrzeni modułów długości te mogą zmieniać, wprowadzając jeszcze większą złożoność.

O kształcie przestrzeni modułów dla grafów danego rzędu decydują relacje między grafami. Gdy poruszasz się po przestrzeni, pobliskie wykresy powinny być podobne i płynnie przechodzić jeden w drugi. Ale te relacje są skomplikowane, pozostawiając przestrzeń modułów z matematycznie niepokojącymi cechami, takimi jak obszary, w których trzy ściany przestrzeni modułów przechodzą przez siebie.

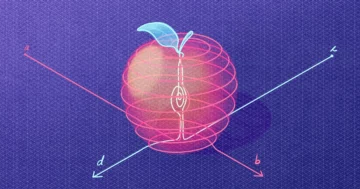
Matematycy mogą badać strukturę przestrzeni lub kształtu za pomocą obiektów zwanych klasami kohomologii, które mogą pomóc odkryć, w jaki sposób przestrzeń jest złożona. Weźmy na przykład jeden z ulubionych kształtów matematyków, pączek. Na pączku klasy kohomologii są po prostu pętlami.

Na powierzchni pączka można narysować kilka różnych rodzajów pętli: Pętla 1 otacza centralny otwór pączka; pętla 2 nici przez otwór; trzecia „trywialna” pętla znajduje się na boku pączka.

Jednak nie wszystkie klasy kohomologii są sobie równe. Pętla znajdująca się na zewnątrz pączka — podobnie jak trzecia pętla — zawsze może się przesuwać lub kurczyć, aby uniknąć przecięcia się z inną pętlą. To czyni ją „trywialną” klasą kohomologii.

Ale pętle 1 i 2 mówią znacznie więcej o strukturze pączka — istnieją tylko dzięki dziurze. Aby matematycznie dostrzec różnicę, możesz użyć przecięć, wyjaśniła Margalit. Pętle 1 i 2 mogą przesuwać się po powierzchni pączka, ale jeśli nie zmusisz ich do całkowitego oderwania się od powierzchni, zawsze będą się przecinać. Ponieważ te dwie pętle mają partnerów, których nie mogą nie przekroczyć, są to „nietrywialne” klasy kohomologii.

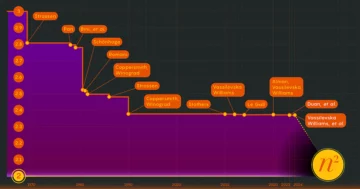
Inaczej niż w przypadku pączka, matematycy nie mogą znaleźć klas kohomologii w przestrzeniach modułów grafów po prostu rysując obrazek. Przy tak ogromnej liczbie wykresów przestrzenie modułów są trudne do opanowania, powiedziała Nathalie Wahl, matematyk z Uniwersytetu w Kopenhadze. „Bardzo szybko, komputer już nie może pomóc” – powiedziała. Rzeczywiście, istniała tylko jedna nietrywialna klasa kohomologii o nieparzystych wymiarach jawnie obliczone (w 11 wymiarach), wraz z garstką parzystych.

Vogtmann i Borinsky udowodnili, że istnieje ogromna liczba klas kohomologii, które leżą w przestrzeni modułów grafów danego rzędu — nawet jeśli nie możemy ich znaleźć. „Wiemy, że jest ich mnóstwo i wiemy o jednym” – powiedział Wahl, nazywając ten stan rzeczy „śmiesznym”.

Zamiast bezpośrednio pracować z klasami kohomologii, Borinsky i Vogtmann badali liczbę zwaną charakterystyką Eulera. Ta liczba zapewnia rodzaj pomiaru przestrzeni modułów. Możesz modyfikować przestrzeń modułów w określony sposób bez zmiany jej charakterystyki Eulera, czyniąc charakterystykę Eulera bardziej dostępną niż same klasy kohomologii. I to właśnie zrobili Borinsky i Vogtmann. Zamiast bezpośrednio pracować z przestrzenią modułów grafów, badali „kręgosłup” — zasadniczo szkielet całej przestrzeni. Kręgosłup ma tę samą charakterystykę Eulera, co sama przestrzeń modułów i jest łatwiejszy w obsłudze. Obliczenie charakterystyki Eulera na grzbiecie sprowadzało się do przeliczenia dużego zbioru par grafów.

Wgląd Borinsky'ego polegał na wykorzystaniu technik liczenia diagramów Feynmana, które są wykresami przedstawiającymi sposoby interakcji cząstek kwantowych. Kiedy fizycy chcą obliczyć, powiedzmy, prawdopodobieństwo, że zderzenie elektronu z pozytonem wytworzy dwa fotony, muszą suma wszystkich możliwych interakcji które prowadzą do takiego wyniku. Oznacza to uśrednianie wielu diagramów Feynmana, motywowanie sprytnych strategii liczenia.

„Zdałem sobie sprawę, że tego rodzaju problem można sformułować jako swego rodzaju zabawkowy wszechświat kwantowej teorii pola” — wyjaśnił Borinsky.

Borinsky wyobrażał sobie, że wykresy przedstawiają układy fizyczne w prostej wersji wszechświata, w której oprócz innych założeń istnieje tylko jeden typ cząstek. Ramy kwantowej teorii pola wymagały pewnych poprawek, aby Borinsky i Vogtmann mogli uzyskać właściwą liczbę. Na przykład w kwantowej teorii pola dwa wykresy, które są swoimi lustrzanymi odbiciami, są nie do odróżnienia, powiedział Borinsky. Formuły dodawania diagramów Feynmana obejmują czynniki, które zapewniają, że te wykresy nie zostaną przeliczone. Ale jeśli chodzi o obliczanie charakterystyki Eulera, te wykresy są uważane za różne. "Musimy zagrać w małą grę z symetriami wykresów" - powiedział Borinsky.

Z pewną pomocą programistyczną ze strony fizyka Josa Vermaserena, Borinsky i Vogtmann ostatecznie pokonali tę trudność. W swoim styczniowym artykule udowodnili, że charakterystyka Eulera dla przestrzeni modułów grafów rang n staje się masowo ujemny jako n powiększa się. Oznacza to, że istnieje wiele, wiele nietrywialnych klas kohomologii do odkrycia w każdej przestrzeni modułów.

Chociaż artykuł Borinsky'ego i Vogtmanna nie zawiera dalszych wskazówek na temat tych klas kohomologii, jest to zachęcający wynik dla badaczy, którzy chcą je znaleźć - i być może dodaje dreszczyku emocji podczas polowania. Margalit o klasach kohomologii powiedziała: „Te, które znamy, to po prostu te klejnoty. I za każdym razem, gdy ją znajdziemy, jest to ta piękna rzecz”.