Förstå konfidensintervall med Python

Denna artikel publicerades som en del av Data Science Blogathon.

Innehållsförteckning

1. Beskrivning
2. Konfidensintervall med Z-statistik
3. Tolkning av konfidensintervall
4. Antaganden för CI med z-statistik
5. Konfidensintervall med t-statistik
6. Antaganden för CI med t-statistik
7. Att göra ett t-intervall med parade data
8. z-värde vs t-värde: när ska man använda vad?
9. Konfidensintervall med python
10. Slutanteckning

Beskrivning

Närhelst vi löser ett statistiskt problem är vi oroliga för uppskattningen av populationsparametrar, men oftare än inte är det nästan omöjligt att beräkna populationsparametrar. Det vi istället gör är att ta stickprov från populationen och beräkna provstatistik med förväntan att approximera populationsparametrar. Men hur vet vi om urvalen är sanna representanter för populationen eller hur mycket denna urvalsstatistik avviker från populationsparametrar? Det är här konfidensintervall kommer in i bilden. Så, vad är dessa intervaller? Konfidensintervallet är ett intervall av värden som sträcker sig över och under urvalsstatistiken eller så kan vi också definiera det som sannolikheten att ett intervall av värden runt urvalsstatistiken innehåller den sanna populationsparametern.

Konfidensintervall med Z-statistik

Innan vi går djupt in i ämnet, låt oss bekanta oss med några statistiska terminologier.

befolkning: Det är uppsättningen av alla liknande individer. Till exempel befolkningen i en stad, studenter på en högskola, etc.

prov: Det är en liten uppsättning liknande individer från befolkningen. På samma sätt är ett slumpmässigt urval ett urval som tas slumpmässigt från populationen.

parametrar: Medel(mu), standardavvikelser(sigma), proportion(p) härledd från populationen.

statistisk: medelvärde(x bar), standardavvikelse(S), proportioner(p^) som gäller prover.

Z-poäng: det är avståndet för en rådatapunkt på en normalfördelning från medelvärdet normaliserat med std-avvikelse. Getts av: x-mu/sigma

Okej nu är vi redo att dyka djupt in i konceptet med konfidensintervall. Av någon anledning tror jag att det är mycket bättre att förstå begrepp genom relaterbara exempel snarare än råa matematiska definitioner. Så låt oss börja.

anta att du bor i en stad med 100,000 100 invånare och ett val är runt hörnet. Som opinionsmästare måste du prognostisera vem som kommer att vinna valet antingen blått parti eller gult. Så du ser att det är nästan omöjligt att samla in information från hela befolkningen så att du slumpmässigt väljer 62 personer. I slutet av undersökningen fann du att 62 % av människorna kommer att rösta på gult. Nu är frågan om vi ska dra slutsatsen att gult kommer att vinna med en vinstsannolikhet på 62 % eller att 58 % av hela befolkningen kommer att rösta på gult? Tja, svaret är NEJ. Vi vet inte säkert hur långt vår uppskattning är från den sanna parametern, om vi tar ett annat prov kan resultatet bli 65% eller XNUMX%. Så vad vi kommer att göra istället är att hitta en rad värden runt vår provstatistik som med största sannolikhet kommer att fånga den sanna populationsandelen. Här avser andelen procentandelen av

                                                                   bilden tillhör författaren

Om vi ​​nu tar hundra sådana prov och plottar provandelen för varje prov får vi en normalfördelning av provtagningsproportioner och medelvärdet av fördelningen kommer att vara det mest ungefärliga värdet av populationsandelen. Och vår uppskattning kan ligga var som helst på fördelningskurvan. Enligt 3-sigma-regeln vet vi att cirka 95% av de slumpmässiga variablerna ligger inom 2 std-avvikelser från medelvärdet av fördelningen. Så kan vi dra slutsatsen att sannolikheten att p^ är inom 2 std avvikelser från p är 95 %. Eller så kan vi också konstatera att sannolikheten för att p är inom 2 std avvikelser under och över p^ också är 95%. Dessa två uttalanden är i praktiken likvärdiga. Dessa två punkter under och över p^ är våra konfidensintervall.

                                                           bilden tillhör författaren

Om vi ​​på något sätt kan hitta sigma kan vi beräkna vårt nödvändiga intervall. Men sigma här är populationsparametern och vi vet att det ofta är nästan omöjligt att beräkna så istället använder vi provstatistik dvs standardfel. Detta ges som

där p^= provandel, n=antal prover

SE =√(0.62 . 0.38/100) = 0.05

så, 2xSE = 0.1

Konfidensintervall för vår data är (0.62-0.1,0.62+0.1) eller (0.52,0.72). Eftersom vi har tagit 2xSE översätts detta till 95 % konfidensintervall.

Nu är frågan vad om vi vill skapa ett 92% konfidensintervall? I föregående exempel multiplicerade vi 2 med SE för att konstruera ett 95 % konfidensintervall, denna 2 är z-poängen för ett 95 % konfidensintervall (exakt värde är 1.96) och detta värde kan hittas från en z-tabell. Det kritiska värdet för z för ett 92 % konfidensintervall är 1.75. Hänvisa till detta artikel för en bättre förståelse av z-score och z-table.

Intervallet ges av: (p^ + z*.SE , p^-z*.SE).

Om i stället för provproportion medelvärde ges kommer standardfelet att vara sigma/sqrt(n). Här sigma är populationens std-avvikelse eftersom vi ofta inte har använder vi stickprovsstd-avvikelse istället. Men det observeras ofta att denna typ av uppskattning där medelvärdet ges resultatet tenderar att vara lite partisk. Så i fall som detta är det att föredra att använda t-statistik istället för z-statistik.

Den allmänna formeln för ett konfidensintervall med z-statistik ges av

Här avser statistiken antingen provmedelvärde eller provandel. sigma_s är populationens standardavvikelse.

Tolkning av konfidensintervall

Det är verkligen viktigt att tolka konfidensintervall korrekt. Tänk på det tidigare exemplet med enkät där vi beräknade att vårt 95 % konfidensintervall var (0.52,0.62, 95). Vad betyder det? Tja, ett 95 % konfidensintervall betyder att om vi drar n urval från populationen så kommer 95 % av tiden att det härledda intervallet innehåller den sanna populationsproportionen. Kom ihåg att ett 95 % konfidensintervall inte betyder att det finns en 90 % sannolikhet att intervallet innehåller den sanna populationsandelen. Till exempel, för ett 10 % konfidensintervall om vi drar 9 urval från en population så kommer 10 av XNUMX gånger nämnda intervall att innehålla sann populationsparameter. Titta på bilden nedan för en bättre förståelse.

                                                            bilden tillhör författaren

Antaganden för konfidensintervall med hjälp av Z-statistik

Det finns vissa antaganden vi behöver leta efter för att konstruera ett giltigt konfidensintervall med hjälp av z-statistik.

1. Slumpmässigt urval: Urvalet måste vara slumpmässigt. Det finns olika urvalsmetoder som stratifierat urval, enkelt slumpmässigt urval, klusterprov för att få slumpmässiga urval.
2. Normalt tillstånd: Datan måste uppfylla detta villkor np^>=10 och n.(1-p^)>=10. Det betyder i huvudsak att vår urvalsfördelning av urvalsmedelvärden måste vara normal, inte skev på någon sida.
3. Oberoende: Urvalen måste vara oberoende. Antalet prover måste vara mindre än eller lika med 10 % av den totala populationen eller om provtagningen görs med ersättning.

Konfidensintervall med T-statistik

Vad händer om urvalsstorleken är relativt liten och populationens standardavvikelse inte ges eller inte kan antas? Hur konstruerar vi ett konfidensintervall? Tja, det är där t-statistik kommer in. Grundformeln för att hitta konfidensintervall här förblir densamma med bara z* ersatt med t*. Den allmänna formeln ges av

där S = provets standardavvikelse, n = antal prover

Anta att du var värd för en fest och du vill uppskatta den genomsnittliga konsumtionen av öl för dina gäster. Så du får ett slumpmässigt urval av 20 individer och mätte ölkonsumtionen. Provdata är symmetriska med ett medelvärde 0f 1200 ml och standardavvikelse på 120 ml. Så nu vill du konstruera ett 95% konfidensintervall.

Så vi har provstd-avvikelse, antalet prover och provmedelvärde. Allt vi behöver är t*. Så, t* för ett 95 % konfidensintervall med en frihetsgrad på 19(n-1 = 20-1) är 2.093. Så vårt nödvändiga intervall är efter beräkningen är (1256.16, 1143.83) med en felmarginal på 56.16. Hänvisa till detta video för att veta hur man läser t-tabellen.

Antaganden för CI med T-statistik

I likhet med fallet med z-statistik även här i fallet med t-statistik finns det några villkor som vi måste se upp med i givna data.

1. Urvalet måste vara slumpmässigt
2. Provet måste vara normalt. För att vara normal bör urvalsstorleken vara större eller lika med 30 eller om det överordnade datasetet dvs populationen är ungefär normal. Eller om provstorleken är under 30 måste fördelningen vara ungefär symmetrisk.
3. Individuella observationer måste vara oberoende. Det betyder att den följer 10%-regeln eller att provtagningen görs med ersättning.

Göra ett T-intervall för parade data

Hittills har vi bara använt ett urvalsdata. Nu ska vi se hur vi kan konstruera ett t-intervall för parade data. I parade data gör vi två observationer på samma individ. Till exempel att jämföra pre-test och post-test betyg för studenter eller data om effekten av ett läkemedel och placebo på en grupp personer. I parade data hittade vi skillnaden mellan de två observationerna i den tredje kolumnen. Som vanligt kommer vi att gå igenom ett exempel för att förstå detta koncept också,

F. En lärare försökte utvärdera effekten av en ny läroplan på testresultatet. Nedan följer resultaten av observationerna.

                                                      bilden tillhör författaren

Eftersom vi avser att hitta intervall för medelskillnaden behöver vi bara statistiken för skillnaderna. Vi kommer att använda samma formel som vi använde tidigare

statistik +- (kritiskt värde eller t-värde) (standardavvikelse för statistik)

x_d = medelvärdet av skillnaden, S_d = prov std-avvikelse, för en 95% CI med en frihetsgrad 5 t* ges av 2.57. Felmarginalen = 0.97 och konfidensintervallet (4.18,6.13).

Tolkning: Från ovanstående uppskattningar som vi kan se innehåller konfidensintervallet inte noll eller negativa värden. Så vi kan dra slutsatsen att den nya läroplanen hade en positiv inverkan på elevernas provprestationer. Om det bara hade negativa värden skulle vi kunna säga att läroplanen hade en negativ inverkan. Eller om den innehöll noll så kan det finnas en möjlighet att skillnaden var noll eller ingen effekt av läroplanen på provresultaten.

Z-värde vs T-värde

Det är mycket förvirring i början om när man ska använda vad. Tumregeln är när urvalsstorleken är >= 30 och populationens standardavvikelse är känd för att använda z-statistik. Om urvalsstorleken är < 30 använd t-statistik. I det verkliga livet har vi inga populationsparametrar så vi kommer att välja z eller t baserat på urvalsstorlek.

Med mindre sampel(n<30) gäller inte den centrala LImit-satsen, och en annan fördelning som kallas Students t-fördelning används. T-fördelningen liknar normalfördelningen men tar olika former beroende på provstorleken. Istället för z-värden används t-värden som är större för mindre sampel, vilket ger en större felmarginal. Eftersom ett litet urval blir mindre exakt.

Konfidensintervall med Python

Python har ett stort bibliotek som stöder alla typer av statistiska beräkningar som gör vårt liv lite enklare. I det här avsnittet kommer vi att titta på uppgifterna om småbarns sömnvanor. De 20 deltagarna i dessa observationer var friska, uppförde sig normalt och hade inga sömnstörningar. Vårt mål är att analysera läggtiden för småbarn som sover och inte sover.

Referens: Akacem LD, Simpkin CT, Carskadon MA, Wright KP Jr, Jenni OG, Achermann P, et al. (2015) Tidpunkten för dygnsklockan och sömnen skiljer sig mellan småbarn som sover och som inte sover. PLoS ONE 10(4): e0125181. https://doi.org/10.1371/journal.pone.0125181

Vi kommer att importera bibliotek som vi kommer att behöva

importera numpy som np importera pandor som pd från scipy.stats import t pd.set_option('display.max_columns', 30) # set så kan se alla kolumner i DataFrame-importmatematiken

df = pd.read_csv(nap_no_nap.csv) #läsning av data

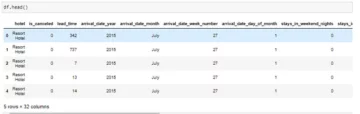
df.head ()

Skapa två 95 % konfidensintervall för den genomsnittliga läggtiden, ett för småbarn som sover och ett för småbarn som inte gör det. Först kommer vi att isolera kolumnen "natt läggdags" för de som tuppar in i en ny variabel och de som inte tuppar in i en annan ny variabel. Sängtiden här är decimaliserad.

bedtime_nap = df['natt läggdags'].loc[df['tupplur'] == 1] sänggående_ingen_lur = df['natt läggdags'].loc[df['tupplur'] == 0]

print(len(bedtime_nap))

print(len(bedtime_no_nap))

utgång: 15 n 5

Nu hittar vi provet genomsnittlig läggtid för tupplur och no_nap.

nap_mean_bedtime = bedtime_nap.mean() #20.304 no_nap_mean_bedtime = bedtime_no_nap.mean() #19.59

Nu hittar vi provets standardavvikelse för X_nap och X_{ingen tupplur} 

nap_s_bedtime = np.std(bedtime_nap,ddof=1) no_nap_s_bedtime = np.std(bedtime_no_nap,ddof=1)

Obs: ddof-parametern är inställd på 1 för sample std dev, annars blir den population std dev.

Nu hittar vi provet standardfel för X_nap och X_{ingen tupplur} 

nap_se_mean_bedtime = nap_s_bedtime/math.sqrt(len(bedtime_nap)) #0.1526 no_nap_se_mean_bedtime = no_nap_s_bedtime/math.sqrt(len(bedtime_no_nap)) #0.2270

Så långt har det gått bra, nu eftersom urvalsstorleken är liten och vi inte har en standardavvikelse för populationsandel kommer vi att använda t*-värdet. Ett sätt att hitta t*-värdet är att använda scipy.stats t.ppf fungera. Argumenten för t.ppf() är q = procent, df = frihetsgrad, skala = std dev, loc = medelvärde. Eftersom t-fördelningen är symmetrisk för ett 95 % konfidensintervall kommer q att vara 0.975. Hänvisa till detta för mer info om t.ppf().

nap_t_star = t.ppf(0.975,df=14) #2.14 no_nap_t_star = t.ppf(0.975,df=5) #2.57

Nu kommer vi att lägga till bitarna för att äntligen konstruera vårt konfidensintervall.

nap_ci_plus = nap_mean_bedtime + nap_t_star*nap_se_bedtime

nap_ci_minus = nap_mean_bedtime – nap_t_star*nap_se_bedtime

print(nap_ci_minus,nap_ci_plus)

no_nap_ci_plus = no_nap_mean_bedtime + no_nap_t_star*nap_se_bedtime

no_nap_ci_minus = no_nap_mean_bedtime – no_nap_t_star*nap_se_bedtime

print(no_nap_ci_minus,no_nap_ci_plus)

utdata: 19.976680775477412 20.631319224522585 18.95974084563192 20.220259154368087

tolkning: 

Från ovanstående resultat drar vi slutsatsen att vi är 95 % säkra på att den genomsnittliga läggtiden för småbarn som sover är mellan klockan 19.98 – 20.63 (pm) medan den för småbarn som inte sover är mellan 18.96 – 20.22 (pm). Dessa resultat är enligt vår förväntning att om du tar en tupplur på dagen kommer du att sova sent på natten.

EndNotes

Så det här handlade om enkla konfidensintervall med z- och t-värden. Det är verkligen ett viktigt begrepp att känna till när det gäller statistiska studier. En stor inferentiell statistisk metod för att uppskatta populationsparametrar från provdata. Konfidensintervall är också kopplade till hypotestestning att för en 95 % CI lämnar man 5 % utrymme för anomalier. Om nollhypotesen faller inom konfidensintervallet så blir p-värdet stort och vi kommer inte att kunna förkasta noll. Omvänt, om det faller bortom kommer vi att ha tillräckliga bevis för att förkasta noll och acceptera alternativa hypoteser.

Hoppas ni gillade artikeln och gott nytt år (:

Medierna som visas i den här artikeln ägs inte av Analytics Vidhya och används efter författarens gottfinnande.

Relaterad

Källa: https://www.analyticsvidhya.com/blog/2022/01/understanding-confidence-intervals-with-python/