ทฤษฎีสนามควอนตัม Pries เปิดปริศนาทางคณิตศาสตร์

เมื่อเดือนที่แล้ว คาเรน โวกท์มันน์ และ ไมเคิ่ล โบรินสกี้ โพสต์หลักฐาน ว่ามีโครงสร้างทางคณิตศาสตร์ปริมาณมากในโลกคณิตศาสตร์ที่ไม่สามารถเข้าถึงได้จนบัดนี้ ซึ่งเรียกว่าโมดูลีสเปซของกราฟ ซึ่ง Vogtmann และผู้ทำงานร่วมกัน ครั้งแรกที่อธิบาย ในกลาง 1980s

“นั่นเป็นปัญหาที่ยากสุดๆ มันน่าทึ่งที่พวกเขาสามารถทำได้” Dan Margalit นักคณิตศาสตร์จากสถาบันเทคโนโลยีแห่งจอร์เจียกล่าว

Vogtmann และ Borinsky เริ่มต้นจากคำถามที่ Vogtmann นักคณิตศาสตร์แห่งมหาวิทยาลัย Warwick ถามตัวเองมานานหลายทศวรรษ จากนั้นทั้งคู่ก็จินตนาการถึงประเด็นนี้ในภาษาฟิสิกส์ โดยใช้เทคนิคจากทฤษฎีสนามควอนตัมในการคิดผลลัพธ์

หลักฐานแสดงให้เห็นว่าโครงสร้างบางอย่างมีอยู่ในพื้นที่ moduli แต่ไม่ได้เปิดเผยอย่างชัดเจนว่าโครงสร้างเหล่านั้นคืออะไร ด้วยวิธีนี้ ผลลัพธ์ใหม่ของพวกเขาจึงเหมือนเครื่องตรวจจับโลหะมากกว่ากล้อง — โดยจะแจ้งเตือนพวกเขาว่ามีบางสิ่งที่น่าสนใจซ่อนอยู่ แม้ว่าพวกเขาจะไม่สามารถอธิบายได้ทั้งหมดก็ตาม

คุณสามารถนึกถึงโมดูลีสเปซของกราฟเป็นรูปทรงทางคณิตศาสตร์ที่มีการตกแต่งเพิ่มเติม หากคุณยืนอยู่ที่จุดใดๆ ของรูปร่าง คุณจะเห็นกราฟลอยอยู่เหนือคุณ ซึ่งเป็นกลุ่มของจุดหรือจุดยอดที่เชื่อมกันด้วยขอบ ที่ตำแหน่งต่างๆ บนพื้นที่โมดูลลี กราฟจะเปลี่ยนไป ขอบจะหดหรือโตขึ้น และบางครั้งก็หายไปพร้อมกัน เนื่องจากคุณสมบัติเหล่านี้ Borinsky นักฟิสิกส์คณิตศาสตร์แห่งสถาบันเทคโนโลยีแห่งสหพันธ์สวิสเซอร์แลนด์ ซูริก อธิบายช่องว่างโมดูลีว่าเป็น "กราฟขนาดใหญ่"

“อันดับ” ของกราฟคือจำนวนลูปที่มี สำหรับแต่ละอันดับของกราฟ มีช่องว่างโมดูลี ขนาดของช่องว่างนี้เพิ่มขึ้นอย่างรวดเร็ว — หากคุณกำหนดความยาวของขอบของกราฟ จะมีกราฟ 2 กราฟของอันดับ 15, 3 ของอันดับ 111, 4 ของอันดับ 2,314,204,852 และ 10 ของอันดับ XNUMX บนพื้นที่โมดูลลี ความยาวเหล่านี้สามารถ แตกต่างกันไป ทำให้เกิดความซับซ้อนมากยิ่งขึ้น

รูปร่างของพื้นที่โมดูลลีสำหรับกราฟของอันดับที่กำหนดจะพิจารณาจากความสัมพันธ์ระหว่างกราฟ ในขณะที่คุณเดินไปรอบๆ พื้นที่นั้น กราฟที่อยู่ใกล้เคียงควรคล้ายกัน และควรปรับเปลี่ยนให้สอดคล้องกัน แต่ความสัมพันธ์เหล่านี้มีความซับซ้อน ทำให้สเปซโมดูลูลีมีลักษณะที่ไม่แน่นอนทางคณิตศาสตร์ เช่น บริเวณที่ผนังสามชั้นของสเปซมอดูลีทะลุผ่านกัน

นักคณิตศาสตร์สามารถศึกษาโครงสร้างของปริภูมิหรือรูปทรงโดยใช้วัตถุที่เรียกว่าวิชาโคโฮโมโลยี ซึ่งสามารถช่วยเผยให้เห็นว่าปริภูมิประกอบกันอย่างไร ตัวอย่างเช่น ลองนึกถึงโดนัทรูปทรงโปรดของนักคณิตศาสตร์ ในโดนัท คลาสโคโฮโมโลจีเป็นเพียงการวนซ้ำ

เราสามารถวาดห่วงได้หลายแบบบนพื้นผิวของโดนัท: ห่วงที่ 1 ล้อมรอบรูตรงกลางของโดนัท วน 2 เธรดผ่านรู ห่วง "เล็กน้อย" ที่สามอยู่ที่ด้านข้างของโดนัท

อย่างไรก็ตาม คลาสโคโฮโมโลจีไม่ได้ถูกสร้างขึ้นเท่ากันทั้งหมด ห่วงที่อยู่ด้านนอกของโดนัท เช่น ห่วงที่สาม สามารถเลื่อนไปมาหรือหดเพื่อหลีกเลี่ยงการตัดกันของห่วงอื่น นั่นทำให้มันเป็นคลาส cohomology ที่ "เล็กน้อย"

แต่ลูปที่ 1 และ 2 พูดถึงโครงสร้างของโดนัทมากกว่า - พวกมันมีอยู่เพราะรูเท่านั้น ในการแยกแยะความแตกต่างทางคณิตศาสตร์ คุณสามารถใช้ทางแยกได้ Margalit อธิบาย ลูปที่ 1 และ 2 สามารถเลื่อนไปรอบ ๆ บนพื้นผิวของโดนัทได้ แต่ถ้าคุณไม่บังคับให้มันหลุดออกจากพื้นผิวโดยสิ้นเชิง พวกมันก็จะตัดกันเสมอ เนื่องจากลูปทั้งสองนี้มาพร้อมกับคู่หูที่พวกเขาอดไม่ได้ที่จะข้ามไป พวกเขาจึงเป็นคลาสโคโฮโมโลยีที่ "ไม่สำคัญ"

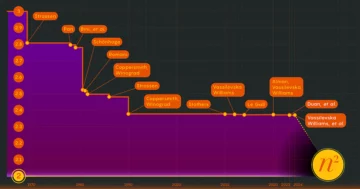
ไม่เหมือนกับโดนัท นักคณิตศาสตร์ไม่สามารถหาคลาสโคโฮโมโลยีบนช่องว่างโมดูลลีของกราฟได้เพียงแค่วาดภาพ Nathalie Wahl นักคณิตศาสตร์จากมหาวิทยาลัยโคเปนเฮเกนกล่าวว่าด้วยกราฟจำนวนมากเช่นนี้ ช่องว่างโมดูลัสจึงเป็นเรื่องยากที่จะรับมือ “เร็วมาก คอมพิวเตอร์ช่วยอะไรไม่ได้อีกแล้ว” เธอกล่าว แท้จริงแล้ว มีคลาสโคโฮโมโลยีที่ไม่น่าสนใจในมิติคี่เพียงคลาสเดียวเท่านั้น คำนวณอย่างชัดเจน (ใน 11 มิติ) พร้อมด้วยแม้แต่หยิบมือเดียว

สิ่งที่ Vogtmann และ Borinsky พิสูจน์ก็คือมีคลาสโคโฮโมโลยีจำนวนมหาศาลที่อยู่ในพื้นที่โมดูลลีของกราฟของอันดับที่กำหนด แม้ว่าเราจะหาไม่เจอก็ตาม “เรารู้ว่ามีจำนวนมาก และเรารู้จักหนึ่งเดียว” วาห์ลกล่าว โดยเรียกสถานการณ์นี้ว่า “ไร้สาระ”

แทนที่จะทำงานกับชั้นเรียนโคโฮโมโลยีโดยตรง Borinsky และ Vogtmann ศึกษาจำนวนที่เรียกว่าคุณลักษณะของออยเลอร์ ตัวเลขนี้เป็นประเภทของการวัดพื้นที่โมดูลี คุณสามารถปรับเปลี่ยนโมดูลูลีสเปซได้ด้วยวิธีบางอย่างโดยไม่ต้องเปลี่ยนคุณลักษณะของออยเลอร์ ทำให้คุณลักษณะของออยเลอร์สามารถเข้าถึงได้มากกว่าคลาสโคโฮโมโลยี และนั่นคือสิ่งที่ Borinsky และ Vogtmann ทำ แทนที่จะทำงานกับโมดูลาลีสเปซของกราฟโดยตรง พวกเขาศึกษา "กระดูกสันหลัง" ซึ่งเป็นโครงกระดูกของสเปซทั้งหมด กระดูกสันหลังมีลักษณะของออยเลอร์เช่นเดียวกับโมดูลัสสเปซและง่ายต่อการใช้งาน การคำนวณลักษณะเฉพาะของออยเลอร์บนกระดูกสันหลังนั้นมาจากการนับกราฟคู่จำนวนมาก

ข้อมูลเชิงลึกของ Borinsky คือการใช้เทคนิคในการนับแผนภาพ Feynman ซึ่งเป็นกราฟที่แสดงถึงปฏิสัมพันธ์ของอนุภาคควอนตัม เมื่อนักฟิสิกส์ต้องการคำนวณ เช่น โอกาสที่การชนกันระหว่างอิเล็กตรอนกับโพสิตรอนจะทำให้เกิดโฟตอน XNUMX ตัว พวกเขาจำเป็นต้อง รวมการโต้ตอบที่เป็นไปได้ทั้งหมด ที่นำไปสู่ผลลัพธ์นั้น นั่นหมายถึงการหาค่าเฉลี่ยจากไดอะแกรมไฟน์แมนจำนวนมาก กระตุ้นกลยุทธ์การนับที่ชาญฉลาด

"ฉันตระหนักว่าเราสามารถกำหนดปัญหาประเภทนี้ได้เหมือนกับจักรวาลทฤษฎีสนามควอนตัมของเล่น" Borinsky อธิบาย

Borinsky จินตนาการว่ากราฟเป็นตัวแทนของระบบทางกายภาพในจักรวาลแบบง่ายๆ ซึ่งหนึ่งในสมมติฐานอื่นๆ มีอนุภาคเพียงประเภทเดียว กรอบทฤษฎีสนามควอนตัมจำเป็นต้องมีการปรับเปลี่ยนบางอย่างสำหรับ Borinsky และ Vogtmann เพื่อให้ได้จำนวนที่ถูกต้อง ตัวอย่างเช่น ในทฤษฎีสนามควอนตัม กราฟสองกราฟที่เป็นภาพสะท้อนของกันและกันจะแยกไม่ออก Borinsky กล่าว สูตรสำหรับการบวกไดอะแกรมไฟน์แมนประกอบด้วยปัจจัยที่ทำให้กราฟเหล่านี้ไม่ถูกนับเกิน แต่เมื่อต้องคำนวณคุณลักษณะของออยเลอร์ กราฟเหล่านั้นถือว่าแตกต่างออกไป “เราต้องเล่นเกมเล็กๆ น้อยๆ กับกราฟที่สมมาตรกัน” Borinsky กล่าว

ด้วยความช่วยเหลือในการเขียนโปรแกรมจากนักฟิสิกส์ จอส แวร์มาเซเรนในที่สุด Borinsky และ Vogtmann ก็เอาชนะความยากลำบากนี้ได้ ในเอกสารเดือนมกราคม พวกเขาพิสูจน์ว่าคุณลักษณะของออยเลอร์ของสเปซโมดูลาลีของกราฟอันดับ n ได้รับผลลบอย่างมากเช่น n ใหญ่ขึ้น นี่หมายความว่ามีคลาสโคโฮโมโลยีที่ไม่สำคัญมากมายที่จะถูกเปิดโปงภายในพื้นที่โมดูลัสแต่ละแห่ง

แม้ว่าบทความของ Borinsky และ Vogtmann จะไม่มีคำใบ้เพิ่มเติมเกี่ยวกับวิชาโคโฮโมโลยีเหล่านี้ แต่ก็เป็นผลลัพธ์ที่น่ายินดีสำหรับนักวิจัยที่ต้องการค้นหาพวกมัน และบางทีมันอาจจะเพิ่มความตื่นเต้นให้กับการตามล่า มาร์กาลิตแห่งชั้นเรียนโคโฮโมโลยีกล่าวว่า “สิ่งเหล่านี้ที่เรารู้จักเป็นเพียงอัญมณีเหล่านี้ และทุกครั้งที่เราพบมันเป็นสิ่งที่สวยงาม”