Giriş
Sıradan En Küçük Kareler bir optimizasyon tekniğidir. OLS, scikit-learn LinearRegression sınıfı ve perde arkasında numpy.polyfit() işlevi tarafından kullanılan tekniğin aynısıdır. OLS tekniğinin detaylarına geçmeden önce bu konuda yazdığım makaleyi gözden geçirmekte fayda var. Optimizasyon tekniklerinin makine öğrenimi ve derin öğrenmedeki rolü. Aynı yazıda OLS tekniğinin (Bölüm 6) var olma sebebini ve içeriğini kısaca açıkladım. Bu makale büyük ölçüde aynı makalenin devamı niteliğindedir ve okuyucuların aynı makaleye aşina olmaları beklenmektedir.

Kaynak: Pixbay
Öğrenme hedefleri:
Bu yazıda,
- OLS'nin ne olduğunu öğrenin ve matematiksel denklemini anlayın
- Ölçekleyici biçimindeki OLS'ye ve dezavantajlarına genel bir bakış elde edin
- Gerçek zamanlı bir örnek kullanarak OLS'yi anlayın
İçindekiler
- Optimizasyon problemleri nelerdir?
- Neden OLS'ye ihtiyacımız var?
- OLS Algoritmasının Arkasındaki Matematiği Anlamak
- Ölçekleyici formunda OLS Çözümü
- Gerçek bir örnek kullanarak Eylemde OLS
- OLS Çözümünün Ölçekleyici formuyla ilgili sorunlar
- Sonuç
Optimizasyon Problemleri Nelerdir?
Optimizasyon problemleri, bir dizi olası çözümden en iyi çözümü bulmayı içeren matematiksel problemlerdir. Bu problemler tipik olarak, amacın belirli bir amaç fonksiyonunu maksimize etmek veya minimize etmek olduğu maksimizasyon veya minimizasyon problemleri olarak formüle edilir. Amaç fonksiyonu, optimize edilecek miktarı açıklayan matematiksel bir ifadedir ve bir dizi kısıtlama, olası çözümler kümesini tanımlar.
Optimizasyon sorunları, mühendislik, finans, ekonomi ve yöneylem araştırması dahil olmak üzere çeşitli alanlarda ortaya çıkar. Kaynak tahsisi, zamanlama ve portföy optimizasyonu gibi sorunları modellemek ve çözmek için kullanılırlar. Optimizasyon, birçok makine öğrenimi algoritmasının çok önemli bir bileşenidir. Makine öğreniminde, modelin tahminleri ile gerçek değerler arasındaki farkı en aza indiren bir model için en iyi parametre kümesini bulmak için optimizasyon kullanılır. Optimizasyon, makine öğrenimi modellerinin eğitim hızını ve doğruluğunu iyileştirmek için geliştirilen yeni optimizasyon algoritmalarıyla makine öğreniminde aktif bir araştırma alanıdır.
Makine öğreniminde optimizasyonun kullanıldığı bazı örnekler şunları içerir:
- denetimli öğrenmede, optimizasyon, belirli bir eğitim veri kümesi için modelin tahminleri ile gerçek değerler arasındaki farkı en aza indiren bir modelin parametrelerini bulmak için kullanılır. Örneğin, doğrusal regresyon ve lojistik regresyon, modelin katsayılarının en iyi değerlerini bulmak için optimizasyonu kullanır. Ayrıca, karar ağaçları, rastgele ormanlar ve gradyan artırma modelleri gibi bazı modeller, topluluğa yinelemeli olarak yeni modeller eklenerek oluşturulur ve eğitim verilerindeki hatayı en aza indiren yeni modellerin parametrelerini optimize eder.
- Denetimsiz öğrenmede, optimizasyon, verilerdeki temel yapıyı en iyi temsil eden en iyi küme yapılandırmasını veya veri eşlemesini bulmaya yardımcı olur. İçinde kümeleme, verilerdeki kümelerin en iyi yapılandırmasını bulmak için optimizasyon kullanılır. Örneğin, K-Means algoritması, veri noktalarını en yakın küme merkezine yinelemeli olarak yeniden atayan ve küme merkezlerini yeni atanan noktalara göre güncelleyen Lloyd's algoritması adı verilen bir optimizasyon tekniği kullanır. Benzer şekilde, hiyerarşik kümeleme, yoğunluk tabanlı kümeleme ve Gauss karışım modelleri gibi diğer kümeleme algoritmaları da en iyi kümeleme çözümünü bulmak için optimizasyon tekniklerini kullanır. İçinde Boyutsal küçülme, optimizasyon, yüksek boyutlu bir alandan daha düşük boyutlu bir alana en iyi veri eşlemesini bulur. Örneğin Temel Bileşen Analizi (PCA), verilerdeki en fazla varyansı açıklayan orijinal değişkenlerin en iyi doğrusal kombinasyonunu bulmak için bir optimizasyon tekniği olan Tekil Değer Ayrıştırmasını (SVD) kullanır. Ek olarak, Lineer Diskriminant Analizi (LDA) ve t-dağılımlı Stokastik Komşu Gömme (t-SNE) gibi diğer boyut indirgeme teknikleri de verilerin daha düşük boyutlu bir alanda en iyi temsilini bulmak için optimizasyon tekniklerini kullanır.
- Derin öğrenmede, optimizasyon, tipik olarak stokastik gradyan iniş (SGD) veya Adam/Adagrad/RMSProp, vb. gibi gradyan tabanlı optimizasyon algoritmaları kullanılarak yapılan sinir ağları için en iyi parametre setini bulmak için kullanılır.
Neden OLS'ye İhtiyacımız Var?
The Sıradan en küçük kareler (OLS) algoritması, bir doğrusal regresyon modelinin parametrelerini tahmin etmek için bir yöntemdir. OLS algoritması, doğrusal regresyon modelinin kare artıklarının toplamını en aza indiren parametrelerinin (yani katsayıların) değerlerini bulmayı amaçlar. Artıklar, bağımlı değişkenin gözlemlenen değerleri ile bağımsız değişkenler verildiğinde bağımlı değişkenin tahmin edilen değerleri arasındaki farklardır. OLS algoritmasının, hataların normal olarak sıfır ortalama ve sabit varyansla dağıldığını ve bağımsız değişkenler arasında çoklu bağlantı (yüksek korelasyon) olmadığını varsaydığına dikkat etmek önemlidir. Bu varsayımların karşılanmadığı durumlarda Genelleştirilmiş En Küçük Kareler veya Ağırlıklı En Küçük Kareler gibi diğer yöntemler kullanılmalıdır.
OLS Algoritmasının Arkasındaki Matematiği Anlamak
OLS algoritmasını açıklamak için mümkün olan en basit örneği ele almama izin verin. Aşağıdaki 3 veri noktasını göz önünde bulundurun:
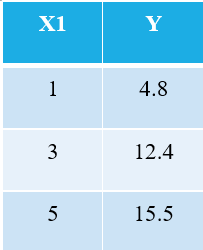
Makine öğrenimine aşina olan herkes, bağımsız değişken olarak X1'den bahsettiğimizi hemen anlayacaktır ("Özellikler"Veya "Öznitellikler"), ve Y bağımlı değişkendir (aynı zamanda "Hedef" or "Sonuç"). Bu nedenle, herhangi bir makinenin genel görevi, X1 & Y arasındaki ilişkiyi bulmaktır. Bu ilişki aslında "öğrendi" gelen makine tarafından TARİH. Bu nedenle, Makine Öğrenimi terimini adlandırıyoruz. Biz insanlar, deneyimlerimizden öğreniyoruz. Benzer şekilde, aynı deneyim makineye veri olarak beslenir.
Şimdi yukarıdaki 3 veri noktası üzerinden en uygun doğruyu bulmak istediğimizi varsayalım. Aşağıdaki çizim, bu 3 veri noktasını mavi daireler içinde göstermektedir. Ayrıca gösterilen kırmızı çizgi (karelerle birlikte), “ olarak iddia ediyoruz.en uygun çizgi” bu 3 veri noktası üzerinden. Ayrıca karşılaştırma için "uyumsuz" bir çizgi (sarı çizgi) gösterdim.
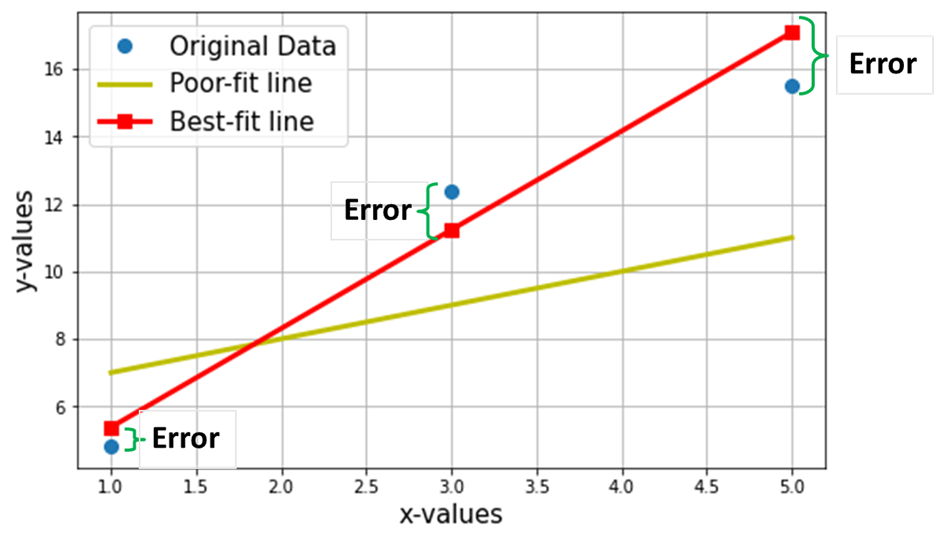
Net amaç, denklemini bulmaktır. En Uygun Düz Çizgi (yukarıdaki tabloda belirtilen bu 3 veri noktası aracılığıyla).

En uygun çizginin denklemidir (yukarıdaki grafikte kırmızı çizgi), burada w1 = çizginin eğimi; w0 = hattın kesilmesi.
Makine öğreniminde bu en uygun duruma doğrusal Gerileme (LR) modeli ve w0 ve w1 de denir model ağırlıkları veya model katsayıları.
Yukarıdaki çizimdeki kırmızı kareler, Doğrusal Regresyon modelinden (Y^) tahmin edilen değerleri temsil eder. Elbette tahmin edilen değerler, Y'nin (mavi daireler) gerçek değerleri ile aynı DEĞİLDİR. Dikey fark, herhangi bir i veri noktası için (aşağıdaki resme bakın) tarafından verilen tahmindeki hatayı temsil eder.
![]()
Şimdi, bu en uygun çizginin tahmin için minimum hataya sahip olacağını iddia ediyorum (olası tüm sonsuz rasgele “zayıf uyum” çizgileri arasında). Tüm veri noktalarındaki bu toplam hata şu şekilde ifade edilir: Ortalama Karesel Hata (MSE) İşlevihangisi olacak asgari en uygun hat için.
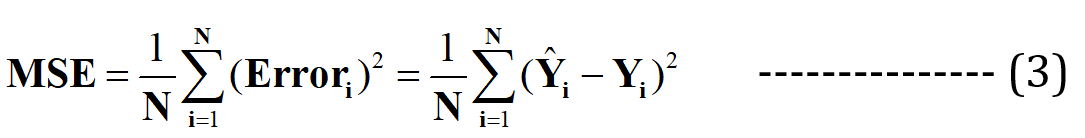
N = Toplam sayı veri kümesindeki veri noktalarının sayısı (mevcut durumda 3'tür)
Herhangi bir miktarın minimize edilmesi veya maksimize edilmesi matematiksel olarak Optimizasyon Problemi, ve dolayısıyla çözüm (minimum/maksimumun bulunduğu nokta) değişkenlerin optimal değerlerini ifade eder.

Doğrusal regresyon kısıtlamasız optimizasyona bir örnektir, tarafından verilen:
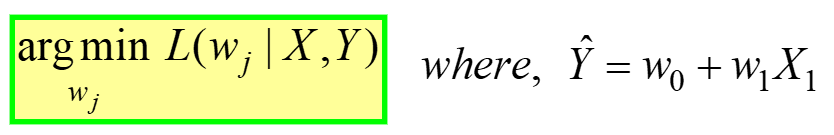 ---- (4)
---- (4)
Bu, “Bul” olarak okunur optimal ağırlıklar (wj) bunun için MSE Kayıp fonksiyonu (yukarıdaki denklem 3'te verilmiştir) minimum değer, Bir için VERİLEN X, Y verileribaşlıklı bir kılavuz yayınladı (makalenin başındaki ilk tabloya bakın). L(wj) X veya Y'nin değil, model ağırlıklarının bir fonksiyonu olan MSE Kaybını temsil eder. Unutmayın, X & Y sizin VERİLERİNİZDİR ve SABİT olması gerekir! “j” alt simgesi, j'inci model katsayısını/ağırlığını temsil eder.
Y^ = w için ikame edildikten sonra0 +w1X1 denklemde 3 yukarıda, son MSE Kayıp Fonksiyonu (L) şu şekilde görünür:
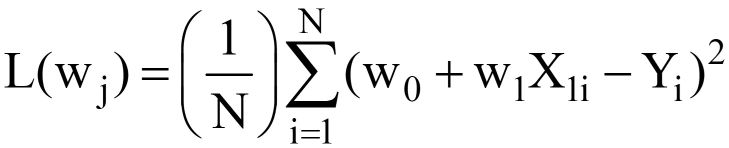 ---- (5)
---- (5)
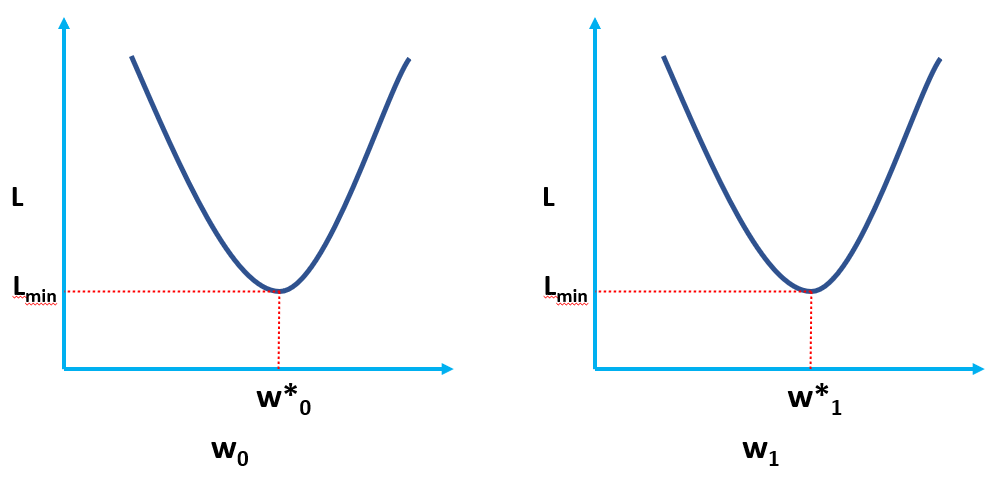
Açıkçası, L, model ağırlıklarının bir fonksiyonudur (w0 & w1), optimal değerlerini L'yi küçülterek bulmamız gerekir. Optimum değerler aşağıdaki şekilde (*) ile temsil edilir.
Ölçekleyici Formunda OLS Çözümü
eq. Yukarıda verilen 5, ölçekleyici formundaki OLS Kaybı işlevini temsil eder (burada hataların toplamı her veri noktası için OLS algoritması, eşitlikte sunulan optimizasyon problemine analitik bir çözümdür. 4. Bu analitik çözüm aşağıdaki adımlardan oluşur:
1 Adım:

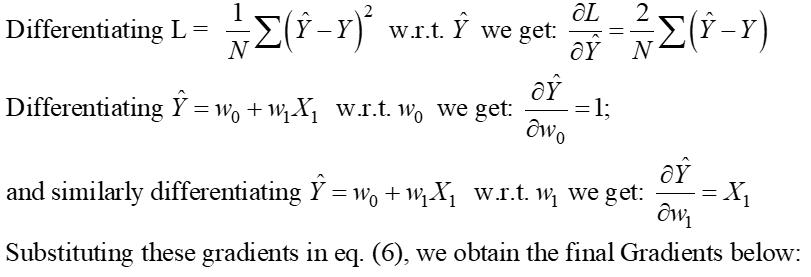

Adım 2: Bu gradyanları sıfıra eşitleyin ve w model katsayılarının optimal değerlerini çözünj.
Bu temel olarak, yukarıdaki şekillerde gösterildiği gibi, optimal değerlerde (L'nin minimum olduğu nokta) Kayıp fonksiyonuna teğetin eğiminin (gradyanların geometrik yorumu) sıfır olacağı anlamına gelir.

Yukarıdaki denklemlerden, “2”yi LHS'den RHS'ye kaydırabiliriz; RHS 0 olarak kalır (0/2 hala 0 olduğu için).


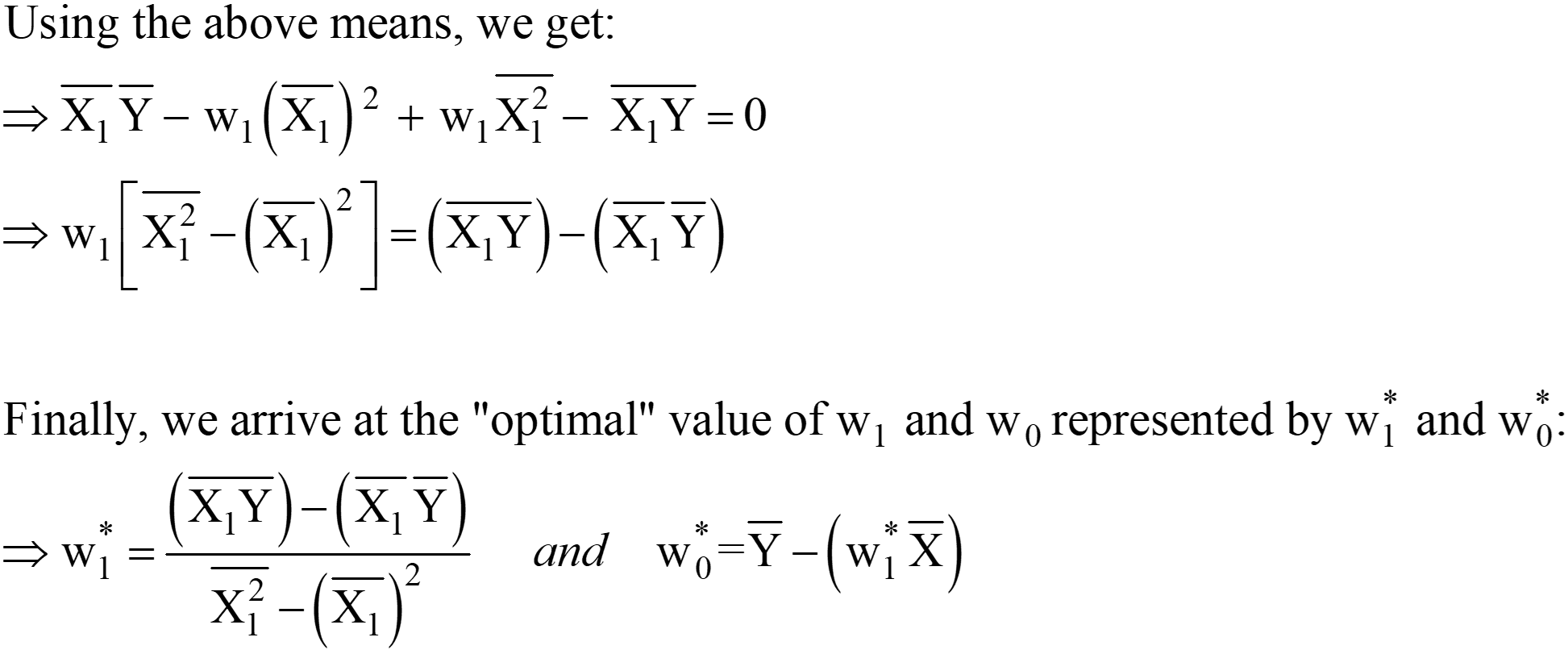
w1* ve w0* için bu ifadeler, Ölçekleyici formundaki nihai OLS Analitik çözümüdür.
Adım 3: Yukarıdaki ortalamayı hesaplayın ve ifadede w1* & w0* yerine koyun.
Veri setimiz için bu değerleri hesaplayalım:
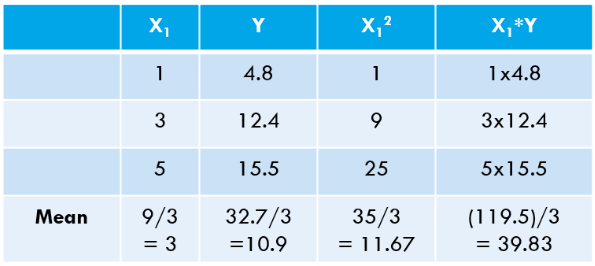
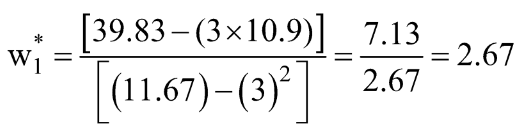
![]()
Python kodunu kullanarak aynı şeyi hesaplayalım:
[ÇIKTI]: "En uygun" Doğrunun Denklemi: 2.675 x + 2.875
"Elle hesaplanan" değerlerimizin, NumPy kullanılarak elde edilen eğim ve kesişim değerleriyle çok yakından eşleştiğini görebilirsiniz (küçük fark, el hesaplamalarımızdaki yuvarlama hatalarından kaynaklanmaktadır). Aynı OLS'nin LinearRegression sınıfının "perde arkasında çalıştığını" da doğrulayabiliriz. scikit-öğrenme paket, aşağıdaki kodda gösterildiği gibi.
# scikit-learn paketinden LinearRegression sınıfını sklearn.linear_model'den içe aktarın import LinearRegression LR = LinearRegression() # LinearRegression sınıfının bir örneğini oluşturun # X ve Y'nizi NumPy Dizileri (sütun vektörleri) olarak tanımlayın X = np.array([1,3,5 ,1,1]).reshape(-4.8,12.4,15.5) Y = np.array([1,1]).reshape(-0) LR.fit(X,Y) # model katsayılarını hesapla LR .intercept_ # eğilim veya kesişme terimi (wXNUMX*)
[Çıktı]: dizi([2.875])
LR.coef_ # eğim terimi (w1*) [Çıktı]: dizi([[2.675]])
Gerçek Bir Örnek Kullanarak Eylemde OLS
Burada Veri Bilimi öğrenirken en sık karşılaşılan veri kümelerinden biri olan Boston House Pricing veri kümesini kullanıyorum. Amaç, bir Doğrusal Regresyon Modeli Aşağıda belirtilen 13 özelliğe/özniteliğe dayalı olarak Konut fiyatlarının medyan değerini tahmin etmek.
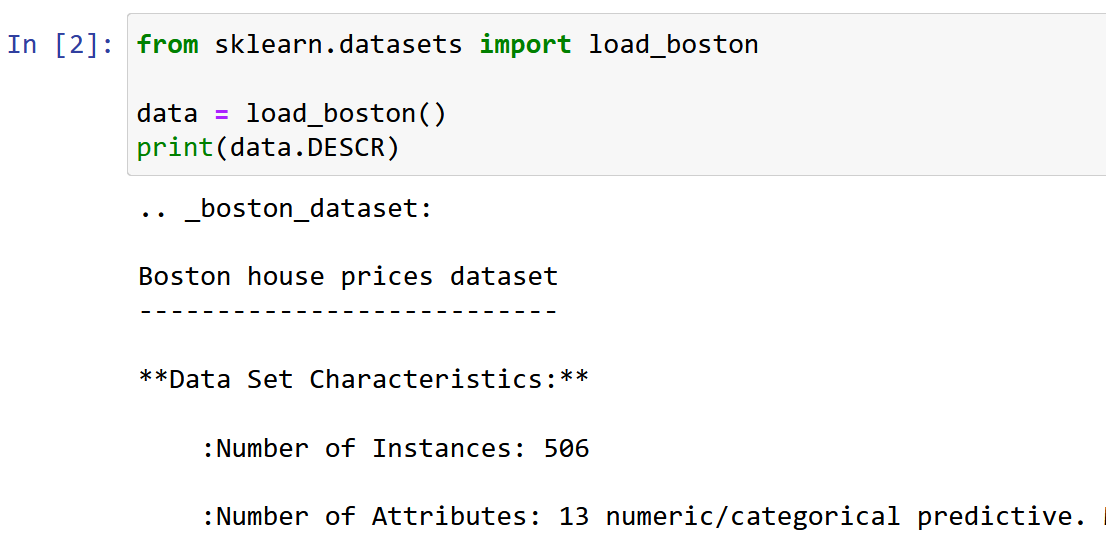
Veri kümesini içe aktarın ve keşfedin.
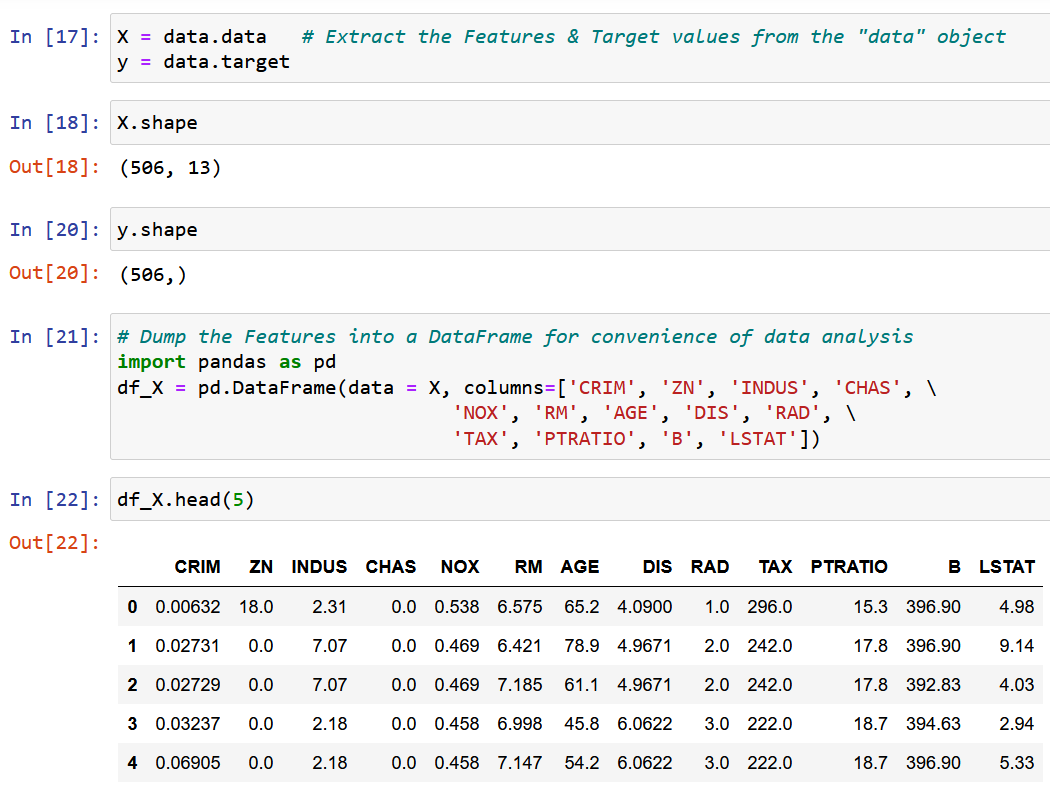
Belirli bir bölgedeki ortalama oda büyüklüğü olan tek bir özellik RM'yi çıkaracağız ve bunu y hedef değişkenine (ev fiyatının medyan değeri) uyduracağız.
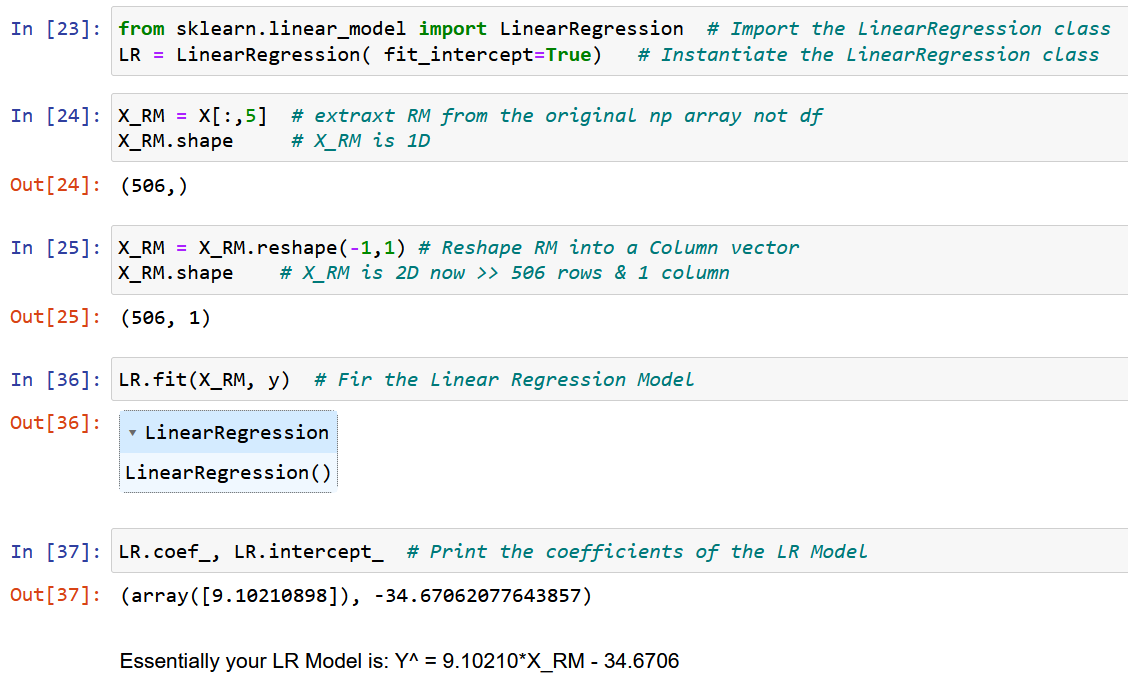
Şimdi saf NumPy kullanalım ve yukarıdaki w0 & w1 model katsayılarının optimal değerleri için türetilen ifadeleri kullanarak model katsayılarını hesaplayalım (Adım 2'nin sonu).
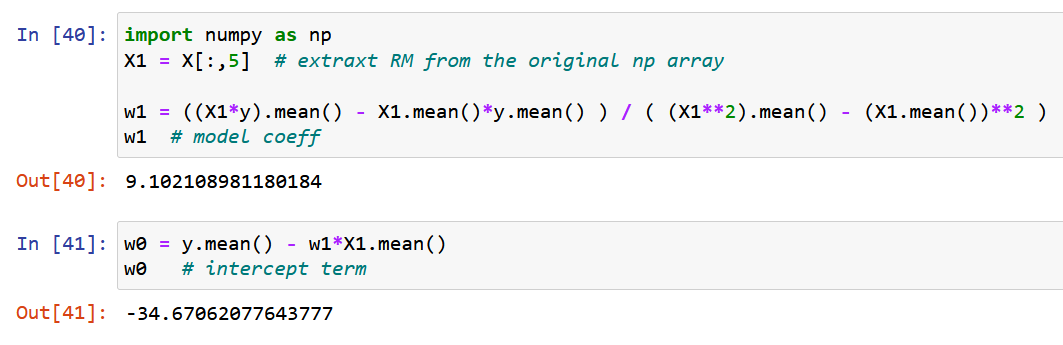
Son olarak orijinal verileri aşağıda verildiği gibi en uygun doğru ile birlikte çizelim.
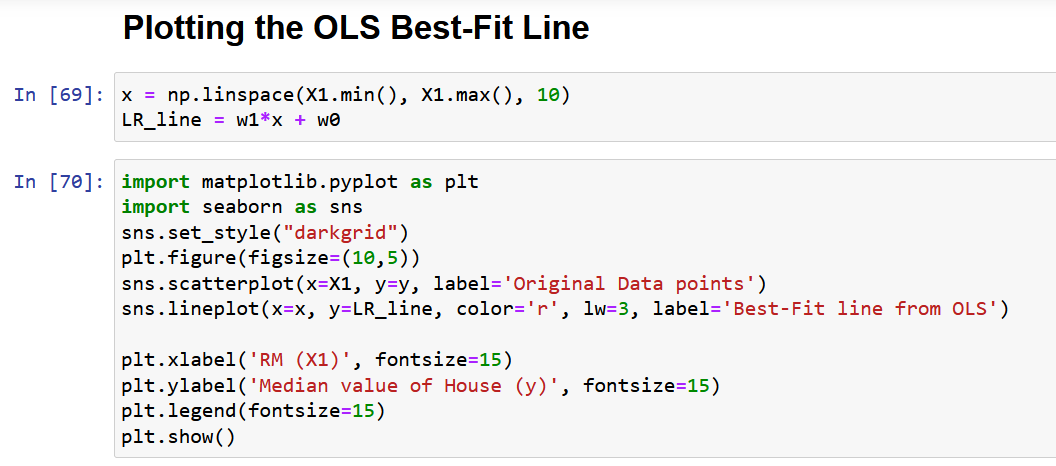

OLS Çözümünün Ölçekleyici Formu ile ilgili sorunlar
Son olarak, 4. bölümde açıklandığı gibi, yukarıdaki yaklaşımla ilgili ana sorunu tartışmama izin verin. Yukarıda bahsedilen veri setinden de görebileceğiniz gibi, herhangi bir gerçek hayattaki veri setinin birden çok özelliği olacaktır. Yukarıdaki bölümde OLS yöntemini göstermek için yalnızca bir özelliği almamın ana nedeni, özellik sayısı arttıkça gradyan sayısının da artacağı, dolayısıyla eş zamanlı olarak çözülecek denklem sayısının da artacağıydı!
Kesin olmak gerekirse, 13 özellik için (yukarıdaki Boston veri seti), 13 model katsayımız ve bir kesme terimimiz olacak, bu da optimize edilecek toplam değişken sayısını 14'e çıkarıyor. Dolayısıyla, 14 gradyan elde edeceğiz (kısmi türev Bu 14 değişkenin her birine göre kayıp fonksiyonu). Sonuç olarak, 14 denklemi çözmemiz gerekiyor (14. adımda açıklandığı gibi bu 2 kısmi türevi sıfıra eşitledikten sonra). Analitik çözümün karmaşıklığını yalnızca 2 değişkenle zaten fark ettiniz. Açıkçası, size internette bulunan OLS'nin EN ayrıntılı açıklamasını vermeye çalıştım, ancak yine de matematiği özümsemek kolay değil.
Bu nedenle, basit bir deyişle, yukarıdaki analitik çözüm ÖLÇEKLENEBİLİR DEĞİLDİR!
Bu sorunun çözümü, sonraki bir makalede (bu makalenin 2. Kısmı) 7. ve 8. bölümlerde ayrıntılı olarak ele alınacak olan "OLS Çözümünün Vektörleştirilmiş Formu"dur.
Sonuç
Sonuç olarak, OLS yöntemi bir lineer regresyon modelinin parametrelerini tahmin etmek için güçlü bir araçtır. Öngörülen ve gerçekleşen değerler arasındaki farkların karelerinin toplamının minimize edilmesi prensibine dayanmaktadır.
Makaleden bazı önemli çıkarımlar aşağıdaki gibidir:
- OLS çözümü, uygulanmasını ve yorumlanmasını kolaylaştıran ölçekleyici biçimde temsil edilebilir.
- Makale, optimizasyon problemleri kavramını ve regresyon analizinde OLS'ye duyulan ihtiyacı tartıştı ve matematiksel bir formülasyon ve eylem halindeki bir OLS örneği sağladı.
- Makale ayrıca ölçeklenebilirlik ve doğrusallık ve sabit varyans varsayımları gibi OLS çözümünün ölçekleyici formunun bazı sınırlamalarını vurgulamaktadır. Umarım bu makaleden yeni bir şeyler öğrenmişsindir.
Bu makaledeki herhangi bir noktanın/denklemin açıklanması gerektiğini düşünüyorsanız veya başka herhangi bir makine öğrenimi algoritması hakkında bu kadar ayrıntılı yazmamı istiyorsanız lütfen bana bir yorum bırakın.
İlgili bağlantılar
- SEO Destekli İçerik ve Halkla İlişkiler Dağıtımı. Bugün Gücünüzü Artırın.
- Plato blok zinciri. Web3 Metaverse Zekası. Bilgi Güçlendirildi. Buradan Erişin.
- Kaynak: https://www.analyticsvidhya.com/blog/2023/01/a-comprehensive-guide-to-ols-regression-part-1/
- 1
- 10
- 214
- 7
- a
- Hakkımızda
- yukarıdaki
- kesin
- doğruluk
- karşısında
- Action
- aktif
- aslında
- ilave
- Ayrıca
- Sonra
- Amaçları
- algoritma
- algoritmalar
- Türkiye
- tahsis
- zaten
- arasında
- analiz
- Analitik
- ve
- yaklaşım
- ALAN
- göre
- atanmış
- mevcut
- ortalama
- merkezli
- temel olarak
- önce
- arkasında
- kamera ARKASI
- olmak
- altında
- İYİ
- arasında
- önyargı
- Mavi
- artırılması
- boston
- kısaca
- Getiriyor
- yapılı
- çağrı
- denilen
- dava
- durumlarda
- Merkez
- belli
- çevreler
- iddia
- sınıf
- yakından
- Küme
- kümeleme
- kod
- Sütun
- kombinasyon
- yorum Yap
- çoğunlukla
- karşılaştırma
- karmaşıklık
- bileşen
- kapsamlı
- hesaplamak
- kavram
- sonuç
- yapılandırma
- sonuç olarak
- Düşünmek
- sabit
- kısıtlamaları
- bağlam
- devam
- Ilişki
- kurs
- yaratmak
- çok önemli
- akım
- karanlık
- veri
- Veri noktaları
- veri bilimi
- veri kümeleri
- karar
- derin
- tanımlar
- gösterdi
- tasviridir
- bağımlı
- Türevleri
- Türetilmiş
- tarif edilen
- ayrıntı
- ayrıntılar
- gelişmiş
- fark
- farklılıkları
- tartışmak
- tartışılan
- dağıtıldı
- Damla
- her
- ekonomi bilimi
- ya
- ayrıntılı
- Mühendislik
- denklemler
- hata
- Hatalar
- vb
- Eter (ETH)
- örnek
- örnekler
- var
- beklenen
- deneyim
- Deneyimler
- Açıklamak
- açıkladı
- açıklar
- açıklama
- keşfetmek
- ifade
- ifade
- çıkarmak
- tanıdık
- Özellikler(Hazırlık aşamasında)
- Özellikler
- Fed
- Alanlar
- şekil
- rakamlar
- son
- Nihayet
- maliye
- bulmak
- bulma
- bulur
- Ad
- uygun
- takip etme
- şu
- Airdrop Formu
- itibaren
- işlev
- Vermek
- verilmiş
- gol
- gidiş
- gradyanları
- grup
- rehberlik
- yardımcı olur
- Yüksek
- özeti
- umut
- ev
- HTTPS
- İnsanlar
- görüntü
- hemen
- uygulamak
- ithalat
- önemli
- iyileştirmek
- in
- dahil
- Dahil olmak üzere
- Artırmak
- bağımsız
- örnek
- Internet
- yorumlama
- dahil
- IT
- anahtar
- ÖĞRENİN
- öğrenme
- LG
- sınırlamaları
- çizgi
- hatları
- GÖRÜNÜYOR
- kayıp
- makine
- makine öğrenme
- Ana
- yapmak
- Yapımı
- çok
- haritalama
- Maç
- matematiksel
- matematiksel olarak
- matematik
- maksimum genişlik
- Maksimuma çıkarmak
- anlamına geliyor
- adı geçen
- yöntem
- yöntemleri
- minimizasyonu
- minimize
- asgari
- karışım
- model
- modelleri
- çoğu
- çoklu
- gerek
- ihtiyaçlar
- net
- ağlar
- sinirsel
- nöral ağlar
- yeni
- normalde
- numara
- dizi
- nesnel
- hedefleri
- elde
- ONE
- Operasyon
- optimum
- optimizasyon
- optimize
- optimize
- orijinal
- Diğer
- tüm
- genel bakış
- paket
- parametreler
- Bölüm
- Platon
- Plato Veri Zekası
- PlatoVeri
- Nokta
- noktaları
- portföy
- mümkün
- güçlü
- tahmin
- tahmin
- tahmin
- Tahminler
- sundu
- fiyat
- Fiyatlar
- fiyatlandırma
- Anapara
- prensip
- Sorun
- sorunlar
- sağlanan
- Python
- miktar
- rasgele
- Okumak
- okuyucular
- gerçek zaman
- fark
- neden
- tanımak
- Kırmızı
- Referans
- ifade eder
- gerileme
- ilişki
- kalıntılar
- hatırlamak
- temsil etmek
- temsil
- temsil
- temsil
- araştırma
- kaynak
- Rol
- oda
- aynı
- ölçeklenebilirlik
- Sahneler
- Bilim
- scikit-öğrenme
- Bölüm
- bölümler
- set
- SGD
- çalışma
- meli
- gösterilen
- Gösteriler
- benzer şekilde
- Basit
- tek
- tekil
- beden
- eğim
- küçük
- çözüm
- Çözümler
- ÇÖZMEK
- biraz
- bir şey
- uzay
- hız
- Kare
- kareler
- başlama
- adım
- Basamaklar
- Yine
- düz
- yapı
- böyle
- sözde
- tablo
- Bizi daha iyi tanımak için
- Takeaways
- Hedef
- Görev
- teknikleri
- The
- İçinden
- için
- araç
- Toplam
- Eğitim
- Ağaçlar
- gerçek
- tipik
- altında yatan
- anlamak
- Güncellemeler
- us
- kullanım
- değer
- Değerler
- çeşitli
- doğrulamak
- gözle görülür
- Ne
- hangi
- süre
- irade
- sözler
- değerli
- olur
- yazmak
- yazılı
- X
- zefirnet
- sıfır







![İmalatta Yapay Zeka Nedir? [10 Kullanım Durumunu Keşfedin]](https://platoaistream.net/wp-content/uploads/2023/08/what-is-ai-in-manufacturing-explore-10-use-cases-360x194.png)



