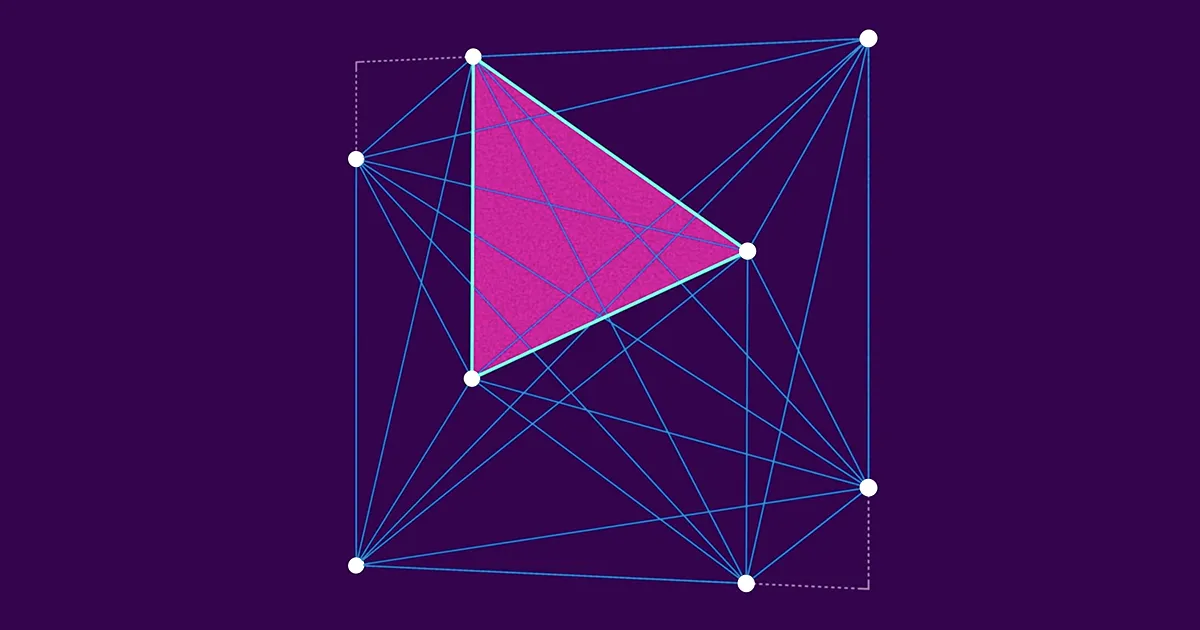
Einleitung
Stellen Sie sich ein Quadrat mit einer Reihe von Punkten vor. Nehmen Sie drei dieser Punkte und Sie können ein Dreieck bilden. Vier Punkte definieren vier verschiedene Dreiecke. Zehn Punkte definieren 120 Dreiecke. Von da an wachsen die Zahlen schnell – 100 Punkte definieren 161,700 verschiedene Dreiecke. Jedes dieser Dreiecke hat natürlich eine bestimmte Fläche.
Hans Heilbronn, ein deutscher Mathematiker, der vor dem Zweiten Weltkrieg aus seinem Land floh und sich in England niederließ, dachte Ende der 1940er Jahre an diese Dreiecke, als er eine Gruppe Soldaten vor seinem Fenster sah. Die Soldaten schienen nicht in Formation zu sein, was ihn zum Nachdenken brachte: Wenn es welche gibt n Soldaten in einem Quadrat, wie groß ist das größtmögliche kleinste Dreieck, das durch drei von ihnen definiert wird? Heilbronn fragte sich, wie man die Soldaten (oder, der mathematischen Einfachheit halber, die Punkte) anordnen könnte, um die Größe des kleinsten Dreiecks zu maximieren.
Das Problem lässt sich einfach formulieren, aber die Fortschritte bei der Lösung des Heilbronner Dreiecksproblems, wie es später genannt wurde, stagnierten, und die Ergebnisse versiegten in den 1980er-Jahren gänzlich. Dann im vergangenen Mai drei Mathematiker – Alex Cohen, Cosmin Pohoata und Dmitrii Sacharow — kündigte a neue Kappe auf die Größe des kleinsten Dreiecks. „Ich denke, es ist ein atemberaubendes Ergebnis“, sagte Anthony Carbery, Mathematiker an der Universität Edinburgh.
Trotz des langen Wartens auf Fortschritte arbeiteten die Forscher jahrelang weiter am Heilbronner Dreiecksproblem, motiviert durch die Verflechtung mit anderen Bereichen der Mathematik. „Die Dinge, mit denen es verbunden ist, machen es lebendig“, sagte Pohoata, Professor an der Emory University in Atlanta. Es steht in engem Zusammenhang mit Problemen über sich schneidende Formen, die wiederum mit der Zahlentheorie und der Fourier-Analyse – der Untersuchung komplizierter Funktionen, die aus einfachen Wellen konstruiert werden – zusammenhängen.
Cohen, ein Doktorand am Massachusetts Institute of Technology, stieß letztes Jahr auf dieses Netz von Verbindungen. Er hatte einen alten Überblick über das Heilbronner Dreiecksproblem von Klaus Roth gelesen, einem weiteren Flüchtling vor den Nazis, der als Junge nach Großbritannien geflohen war. (Roth, der 2015 starb, war der erste britische Mathematiker, der die Fields-Medaille gewann.)
Cohen visualisierte die Ideen aus Roths Umfrage mit einem einfachen Bild: einem Quadrat, das von zwei dicken Streifen durchzogen ist und in deren Mitte jeweils eine dünne Linie verläuft. Als er sein Diagramm studierte, wurde Cohen klar, dass es möglicherweise mit Ideen in Zusammenhang steht, die sein Berater Larry Guth kürzlich bei einem Lesegruppentreffen angesprochen hatte. Aber Guth hatte überhaupt nicht über Dreiecke gesprochen.
„Mir wurde sehr schnell klar, dass diese beiden Methoden im Wesentlichen gleichwertig waren“, sagte Cohen. „Das Dreiecksproblem hat mich wirklich begeistert.“
Eines Tages entdeckte Cohen im Gemeinschaftsraum der Mathematikabteilung des MIT unerwartet, dass Pohoata, der gekommen war, um einen Vortrag zu halten, und Zakharov, ein Kommilitone am MIT, ebenfalls am Heilbronner Dreiecksproblem gearbeitet hatten. Darüber hinaus hatten sie denselben Link gefunden. Die drei begannen zusammenzuarbeiten. Sieben Monate später gelang ihnen der Durchbruch. Ihre Arbeit bringt noch mehr neue Bereiche der Mathematik mit sich. „Sie nutzen eine riesige Menge an Maschinen und unterschiedliche Erkenntnisse“, sagte Thomas Bloom von der Universität Oxford, der sagte, er erwarte, dass das neue Papier „eine Renaissance“ der Fortschritte beim Dreiecksproblem auslösen werde.
Eine Hypothese wurde abgelehnt
Indem Sie drei Punkte sehr nahe beieinander platzieren, können Sie das kleinste Dreieck in einer Anordnung ganz einfach beliebig klein machen. (Im extremsten Fall bilden drei auf einer Linie liegende Punkte ein Dreieck mit einer Fläche von Null.) Schwieriger ist es jedoch, das kleinste Dreieck groß zu halten. Wenn Sie immer mehr Punkte hinzufügen, wird das kleinste Dreieck gezwungenermaßen ziemlich klein – neue Punkte können nur einen bestimmten Abstand zu den vorhandenen haben. Es ist relativ einfach zu zeigen, dass das kleinste Dreieck keine Fläche haben kann, die größer als 1/(n − 2) durch Aufspaltung des Quadrats in nicht überlappende Dreiecke.
Doch Heilbronn meinte, die Grenze sei noch geringer. Er vermutete, dass es, egal wie die Punkte im Quadrat angeordnet waren, kein kleinstes Dreieck mit einer Fläche von mehr als etwa 1/ geben konnte.n2, eine Zahl, die viel schneller schrumpft als n wächst.
Er hat sich geirrt.
1980 gründeten die ungarischen Mathematiker János Komlós, János Pintz und Endre Szemerédi habe ein Muster gefunden von Punkten, deren kleinstes Dreieck eine Fläche von etwas mehr als 1/ hatten2. In einem separaten Artikel, der etwa zur gleichen Zeit veröffentlicht wurde, zeigten sie auch, dass es unmöglich sei, etwas zu arrangieren n Punkte, um ein kleinstes Dreieck zu erstellen, das größer als etwa 1/ istn8/7. Wenn n ist groß, das ist viel kleiner als 1/n, aber viel größer als 1/n2.
Diese Ergebnisse blieben über 40 Jahre bestehen. „Die Verbesserung [der Grenze] in beide Richtungen war bemerkenswert schwierig und erforderte viel technische Analyse und Einfallsreichtum“, sagte Bloom.
„Man gerät sehr, sehr schnell in einen völligen Sumpf von Dingen“, fügte Carbery hinzu.
Während die 1980 entdeckte Konstruktion nach wie vor die mit dem größten bekannten kleinsten Dreieck ist, ist es Cohen, Pohoata und Zakharov zum ersten Mal seit vier Jahrzehnten gelungen, die Obergrenze zu senken.
Konvergente Evolution
Als er Cohen traf, beschäftigte sich Pohoata bereits seit zwei Jahren mit dem Heilbronner Dreiecksproblem. Im Sommer 2020 beauftragte er Sommerforscher der Yale University mit der Arbeit an höherdimensionalen Versionen des Problems – zum Beispiel der Eingrenzung der größten Formen mit kleinstem Volumen, die zwischen in einem dreidimensionalen Würfel verstreuten Punkten erscheinen.
Im Rahmen dieses Projekts überprüfte Pohoata alle früheren Arbeiten zu diesem Problem. Zurück in 1951, Roth hatte die Suche nach kleinen Dreiecken in zwei Teile geteilt: Zuerst ein Punktepaar finden, um die Basis des Dreiecks zu bilden, und dann einen dritten Punkt finden, um das Dreieck zu vervollständigen. Die Strategie umrahmte im Wesentlichen die Suche nach einem großen, kleinsten Dreieck als Untersuchung sich schneidender Punkte und Rechtecke – ein Ansatz, der 1972 von Wolfgang Schmidt verfeinert wurde.
Beim Lesen von Schmidts Artikel erkannte Pohoata einen Zusammenhang mit der High-Low-Methode – einer Technik, die Guth und Mitarbeiter 2017 entwickelt hatten, um die Überlappung zwischen einer Ansammlung rechteckiger Streifen und einer Ansammlung von Scheiben abzuschätzen. „Das war ein wichtiger psychologischer Moment für mich“, sagte er.
Im Jahr 2021 brachte Pohoata Zakharov seine Ideen vor. Die beiden hatten begonnen, gemeinsam zu veröffentlichen, als Sacharow noch in Moskau studierte. „[Zakharov] hat bemerkenswerte Dinge geleistet, als wäre er ein leitender Forscher in jungen Jahren“, sagte Jacob Fox, Mathematiker an der Stanford University.
Zakharov war zunächst pessimistisch, was das Heilbronner Dreiecksproblem angeht. „Ich dachte, dass dieser 8/7 40 Jahre dort oben blieb, also wer bin ich, um ihn zu knacken?“ er sagte. „Ich wollte vor allem verstehen, wie es funktioniert.“
Nachdem sie sich im Oktober 2022 begegnet waren, erkannten Cohen, Pohoata und Zakharov schnell das Hindernis, mit dem Komlós, Pintz und Szemerédi unwissentlich konfrontiert waren. „Es gibt eine sehr spezifische Anordnung der Punkte, die zu diesem Worst-Case-Szenario führt, bei dem sie nicht besser als 8/7 abschneiden können“, sagte Cohen. „Die Punkte können entweder konzentriert oder verteilt sein. Der schlimmste Fall ist, wenn es sich um eine Kombination handelt.“ Bei dieser Anordnung waren die Punkte großräumig verteilt, aber wenn Sie auf winzige Unterquadrate innerhalb des Einheitsquadrats hineinzoomen, würden Sie geordnete Muster erkennen.
Cohen, Pohoata und Zakharov erkannten, dass sie durch die Untersuchung der Dimension der kleinen Punktcluster Fortschritte erzielen könnten. Für Nichtmathematiker sind Dimensionen immer ganze Zahlen: Ein Blatt Papier ist zweidimensional; ein Lehmziegel hat drei Dimensionen.
Die Dinge können seltsam werden, wenn man die Dimension einer Reihe von Punkten berücksichtigt. Ein einzelner Punkt wird normalerweise als nulldimensional betrachtet. Aber zwei endliche Punktmengen können völlig unterschiedliche Strukturen haben. Bei einem könnten 10 Punkte gehorsam in einer geraden Linie marschieren, während bei dem anderen 10 Punkte über das gesamte Einheitsquadrat verteilt sind.
Um die Struktur selbst der seltsamsten Punktmengen zu erfassen, entwickelte der Mathematiker Felix Hausdorff zu Beginn des 20. Jahrhunderts einen neuen Begriff der Dimension. Nach dieser Definition sind 10 Punkte auf einer Linie eindimensional, während 10 Punkte, die gleichmäßig über ein Quadrat verteilt sind, zweidimensional sind. Aber in dieser Welt müssen Dimensionen keine ganzen Zahlen sein, und eine eindimensionale Menge kann nicht linear, sondern fraktal sein und unendlich viele Schichten komplizierter Muster aufweisen. Abhängig von den Details dieser Muster können Punktsammlungen sogar eine Dimension haben, die größer als 0, aber kleiner als 1 ist.
Cohen, Pohoata und Zakharov entdeckten a Satz von 1953 von John Marstrand, der die Schätzung von Komlós, Pintz und Szemerédi im Hinblick auf die Hausdorff-Dimension umformulierte – allerdings nur für Dimensionen größer als 1. Um die Schätzung zu verbessern, müssten Cohen, Pohoata und Zakharov einen Weg finden, Marstrands Ergebnis auf Mengen zu verallgemeinern deren Dimension kleiner als 1 war.
Verbindungen herstellen
Cohen, Pohoata und Zakharov mussten nicht lange nachdenken. Wie es geschah, ein Papier von Tuomas Orponen, Pablo Shmerkin und Hong Wang das war gerade gewesen online veröffentlicht erweiterte Marstrands 70 Jahre alten Satz auf Mengen, deren Dimension kleiner als 1 war.
Cohen erfuhr erst im Februar von der Zeitung. Sobald er dies getan hatte, leitete er es schnell an Pohoata und Zakharov weiter. Ende Mai hatten sie ihre Arbeit online gestellt und damit bewiesen, dass es sich um das kleinste Dreieck unter ihnen handelte n Punkte in einem Einheitsquadrat können niemals größer als 1/ seinn8 / 7 + 1 / 2000.
Shmerkin las das Dreieckspapier aus einer Laune heraus, nachdem er die Ankündigung auf Twitter gesehen hatte. Das Problem des Heilbronner Dreiecks war ihm bis dahin noch nicht einmal bewusst, daher war er überrascht, als er den Hinweis auf seinen Beweis entdeckte. „Dies ist keine direkte Anwendung dessen, was wir tun. Darin steckt eine Menge aufschlussreicher, kreativer und technischer Arbeit“, sagte er. „Für mich war es ein tolles Gefühl.“
Auch Bloom war beeindruckt. „Ich hätte mir dieses Papier lange ansehen können und wäre nie auf den Gedanken gekommen, oh, das trifft auf das Dreiecksproblem zu.“
Während das neue Ergebnis den Exponenten von Komlós, Pintz und Szemerédi nur um einen winzigen Bruchteil verbessert, hat es das lange schwelende Heilbronner Dreiecksproblem wiederbelebt. „Man könnte einen Blick darauf werfen und sagen, gähn, gähn, gähn, es sieht gar nicht so anders aus als das, was man 1982 kannte. Aber seit 1982 ist sehr viel Zeit vergangen“, sagte Carbery.
Durch die Einbeziehung der Hoch-Tief-Methode und der Arbeit von Orponen, Shmerkin und Wang haben Cohen, Pohoata und Zakharov eine neue Reihe von Verbindungen zwischen dem Heilbronner Dreiecksproblem und dem Rest der Mathematik aufgedeckt. Wie Bloom es ausdrückte, wurde das Dreiecksproblem als „ein wirklich schönes, wirklich schwieriges Problem, von dem wir nicht wissen, was wir tun sollen“ betrachtet. Aber sie haben gesagt, dass es mit einer Menge anderer Dinge zusammenhängt.“
Einige glauben, dass die wahre Antwort auf das Heilbronner Dreiecksproblem nicht viel größer sein wird als seine ursprüngliche Vermutung von 1/n2. „Wenn ich Punkte strukturiert darlege, scheitere ich; Wenn ich Punkte auf zufällige Weise verteile, scheitere ich. Es darf nicht zu strukturiert sein, es darf nicht zu zufällig sein, deshalb existiert es wahrscheinlich nicht“, sagte Bloom. Doch Sacharow hofft auf eine andere Antwort. Die Intuitionen, die eine Antwort von 1/ unterstützenn2 seien „irgendwie langweilig“, sagte er. „Mir wäre es sehr lieber, wenn es so wäre n3/2"
- SEO-gestützte Content- und PR-Distribution. Holen Sie sich noch heute Verstärkung.
- PlatoData.Network Vertikale generative KI. Motiviere dich selbst. Hier zugreifen.
- PlatoAiStream. Web3-Intelligenz. Wissen verstärkt. Hier zugreifen.
- PlatoESG. Automobil / Elektrofahrzeuge, Kohlenstoff, CleanTech, Energie, Umwelt, Solar, Abfallwirtschaft. Hier zugreifen.
- PlatoHealth. Informationen zu Biotechnologie und klinischen Studien. Hier zugreifen.
- ChartPrime. Verbessern Sie Ihr Handelsspiel mit ChartPrime. Hier zugreifen.
- BlockOffsets. Modernisierung des Eigentums an Umweltkompensationen. Hier zugreifen.
- Quelle: https://www.quantamagazine.org/the-biggest-smallest-triangle-just-got-smaller-20230908/
- :hast
- :Ist
- :nicht
- :Wo
- ][P
- $UP
- 1
- 10
- 100
- 13
- 2015
- 2017
- 2020
- 2021
- 2022
- 40
- 700
- a
- Über Uns
- Nach
- über
- hinzugefügt
- Hinzufügen
- Nach der
- Alter
- Alle
- bereits
- ebenfalls
- immer
- am
- unter
- Betrag
- an
- Analyse
- und
- angekündigt
- Ein anderer
- beantworten
- Heinrich
- jedem
- erscheinen
- Anwendung
- gilt
- Ansatz
- SIND
- Bereich
- Bereiche
- um
- vereinbart worden
- Anordnung
- AS
- At
- Atlanta
- bewusst
- Base
- BE
- war
- Bevor
- begann
- begonnen
- Glauben
- Besser
- zwischen
- Big
- größer
- Größte
- Blühen
- steckengeblieben
- Bohren
- beide
- gebunden
- Durchbruch
- Brings
- Großbritannien
- Briten
- gebracht
- Haufen
- aber
- by
- namens
- kam
- CAN
- Kann bekommen
- Erfassung
- Häuser
- Menu
- eng
- Cohen
- Zusammenarbeit
- Sammlung
- Produktauswahl
- Kombination
- wie die
- gemeinsam
- abschließen
- uneingeschränkt
- kompliziert
- Konzentriert
- Vernetz Dich
- Sie
- Verbindung
- Verbindungen
- Geht davon
- betrachtet
- Baugewerbe
- könnte
- Land
- Kurs
- Riss
- erstellen
- Kreativ (Creative)
- Tag
- Jahrzehnte
- definieren
- definiert
- Definition
- Abteilung
- Abhängig
- Trotz
- Details
- entwickelt
- DID
- gestorben
- anders
- Abmessungen
- Größe
- Direkt
- Richtung
- entdeckt
- do
- Tut nicht
- Dabei
- Nicht
- nach unten
- jeder
- Früh
- leicht
- Einfache
- Edinburgh
- entweder
- England
- Ganz
- vollständig
- Äquivalent
- im Wesentlichen
- schätzen
- Sogar
- gleichmäßig
- ÜBERHAUPT
- Beispiel
- aufgeregt
- existieren
- vorhandenen
- erwartet
- Extrem
- konfrontiert
- FAIL
- weit
- beschleunigt
- Februar
- Kerl
- Felder
- Finden Sie
- Vorname
- erstes Mal
- Aussichten für
- gezwungen
- unten stehende Formular
- Ausbildung
- gefunden
- vier
- Fuchs
- Fraktion
- für
- Funktionen
- Deutsch
- bekommen
- ABSICHT
- Go
- Abschluss
- groß
- mehr
- Gruppe an
- Wachsen Sie über sich hinaus
- Wächst
- erraten
- hätten
- stockend
- passiert
- hart
- Haben
- he
- ihm
- seine
- Hoffnung
- Ultraschall
- HTML
- HTTPS
- riesig
- Ungarisch
- i
- Ideen
- identifiziert
- if
- ii
- wichtig
- unmöglich
- beeindruckt
- zu unterstützen,
- verbessert
- in
- einarbeiten
- Einfallsreichtum
- anfänglich
- innerhalb
- aufschlussreiche
- Einblicke
- Institut
- in
- IT
- SEINE
- Peter
- nur
- Behalten
- gehalten
- klaus
- Wissen
- bekannt
- grosse
- größer
- höchste
- Nachname
- Letztes Jahr
- Spät
- später
- Lagen
- umwandeln
- LERNEN
- weniger
- LIMIT
- Line
- LINK
- Links
- Lang
- lange Zeit
- aussehen
- sah
- Los
- Senkung
- Maschinen
- gemacht
- Zeitschrift
- um
- Massachusetts
- Massachusetts Institute of Technology
- Mathe
- mathematisch
- Mathematik
- Materie
- Maximieren
- Kann..
- me
- Treffen
- versiegelte
- Methode
- Methoden
- Methoden waren
- Mitte
- könnte
- MIT
- Moment
- Monat
- mehr
- Moskau
- vor allem warme
- meist
- motiviert
- viel
- Need
- hört niemals
- Neu
- schön
- nicht
- Normalerweise
- Notion
- Anzahl
- Zahlen
- Hindernis
- Oktober
- of
- oh
- Alt
- on
- einmal
- EINEM
- Einsen
- Online
- einzige
- or
- Auftrag
- Original
- Andere
- aussen
- übrig
- Oxford
- Paar
- Papier
- Teil
- besondere
- Teile
- Bestanden
- passt
- Muster
- pessimistisch
- ein Bild
- Platzierung
- Plato
- Datenintelligenz von Plato
- PlatoData
- Points
- Punkte
- möglich
- gepostet
- bevorzugen
- ziemlich
- Vor
- wahrscheinlich
- Aufgabenstellung:
- Probleme
- Professor
- Fortschritt
- Projekt
- Beweis
- veröffentlicht
- Publishing
- setzen
- schnell
- zufällig
- Lesen Sie mehr
- Lesebrillen
- realisiert
- wirklich
- kürzlich
- Referenz
- raffiniert
- Flüchtling
- bezogene
- verhältnismäßig
- bleibt bestehen
- bemerkenswert
- falls angefordert
- Forschungsprojekte
- Forscher
- REST
- Folge
- Die Ergebnisse
- Zimmer
- Laufen
- Said
- gleich
- sah
- Skalieren
- verstreut
- Szenario
- Suche
- sehen
- Sehen
- Senior
- getrennte
- kompensieren
- Sets
- "Settled"
- sieben
- Formen
- Blatt
- erklären
- zeigte
- Einfacher
- Einfachheit
- da
- Single
- Größe
- klein
- kleinere
- kleinste
- So
- bis jetzt
- einige
- Bald
- spezifisch
- gespalten
- Verbreitung
- quadratisch
- Stanford
- Stanford Universität
- Bundesstaat
- blieb
- Immer noch
- Strategie
- Struktur
- strukturierte
- Strukturen
- Schüler und Studenten
- Die Kursteilnehmer
- sucht
- Studie
- Studieren
- Atemberaubende
- Sommer
- Support
- überrascht
- Umfrage
- Nehmen
- Reden
- sprechen
- Technische
- Technische Analyse
- Technologie
- zehn
- AGB
- als
- zur Verbesserung der Gesundheitsgerechtigkeit
- Das
- ihr
- Sie
- dann
- Theorie
- Dort.
- deswegen
- Diese
- vom Nutzer definierten
- Denken
- Denken
- Dritte
- fehlen uns die Worte.
- diejenigen
- dachte
- nach drei
- dreidimensional
- Krawatten
- Zeit
- zu
- gemeinsam
- auch
- was immer dies auch sein sollte.
- WENDE
- XNUMX
- unbedeckt
- verstehen
- Einheit
- Universität
- University of Oxford
- bis
- auf
- -
- Versionen
- sehr
- warten
- wollte
- Krieg
- wurde
- Wellen
- Weg..
- we
- Netz
- webp
- GUT
- waren
- Was
- Was ist
- wann
- welche
- während
- WHO
- ganze
- deren
- gewinnen
- Fenster
- mit
- .
- WordPress
- Arbeiten
- arbeiten,
- Werk
- weltweit wie ausgehandelt und gekauft ausgeführt wird.
- Wurst
- würde
- Falsch
- Jahr
- Jahr
- U
- jung
- Zephyrnet
- Null











