1QuSoft & CWI, Amsterdam, the Netherlands.
2Blackett Laboratory, Imperial College Prince Consort Rd., London, SW7 2AZ, U.K.
Find this paper interesting or want to discuss? Scite or leave a comment on SciRate.
Abstract
We consider the complexity of the local Hamiltonian problem in the context of fermionic Hamiltonians with $mathcal N=2 $ supersymmetry and show that the problem remains $mathsf{QMA}$-complete. Our main motivation for studying this is the well-known fact that the ground state energy of a supersymmetric system is exactly zero if and only if a certain cohomology group is nontrivial. This opens the door to bringing the tools of Hamiltonian complexity to study the computational complexity of a large number of algorithmic problems that arise in homological algebra, including problems in algebraic topology, algebraic geometry, and group theory. We take the first steps in this direction by introducing the $k$-local Cohomology problem and showing that it is $mathsf{QMA}_1$-hard and, for a large class of instances, is contained in $mathsf{QMA}$. We then consider the complexity of estimating normalized Betti numbers and show that this problem is hard for the quantum complexity class $mathsf{DQC}1$, and for a large class of instances is contained in $mathsf{BQP}$. In light of these results, we argue that it is natural to frame many of these homological problems in terms of finding ground states of supersymmetric fermionic systems. As an illustration of this perspective we discuss in some detail the model of Fendley, Schoutens, and de Boer consisting of hard-core fermions on a graph, whose ground state structure encodes $l$-dimensional holes in the independence complex of the graph. This offers a new perspective on existing quantum algorithms for topological data analysis and suggests new ones.
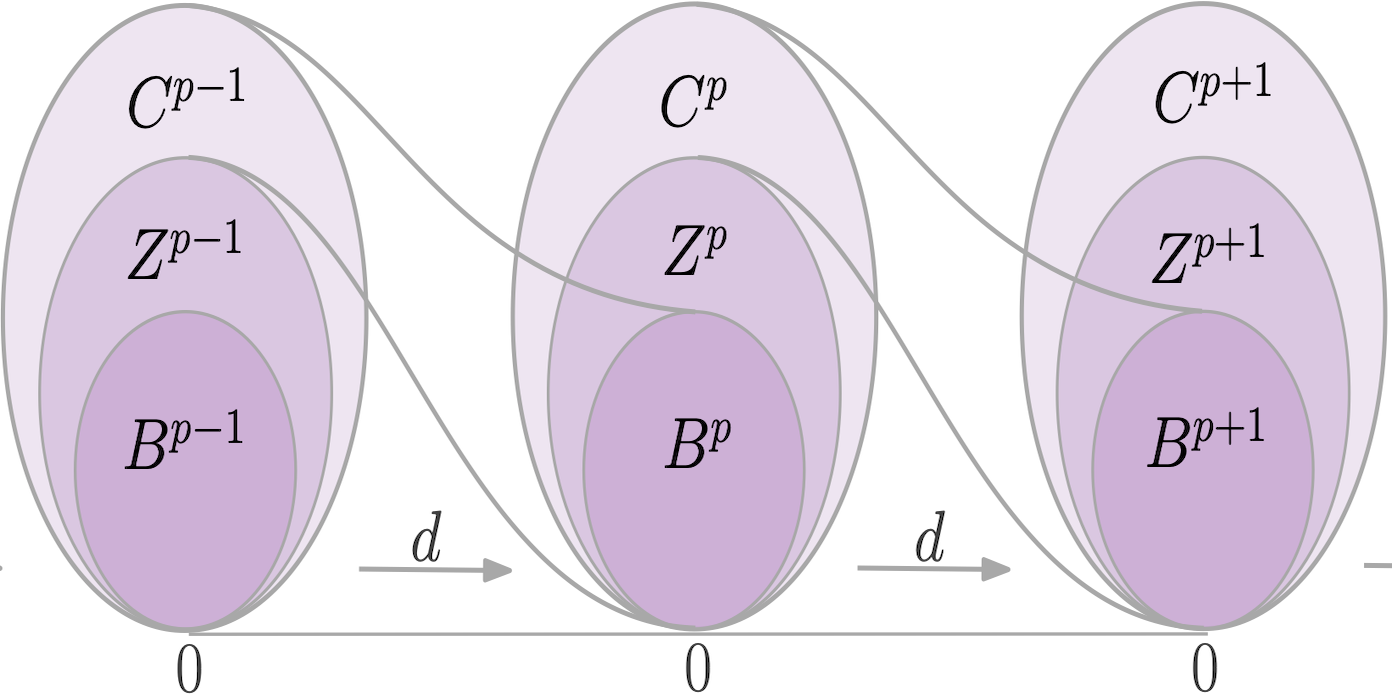
Featured image: Schematic of the relationship between cochains ($C^{p−1}$, $C^p$, $C^{p+1}$), cocycles $Z^{p−1}$, $Z^p$, $Z^{p+1}$, and coboundaries ($B^{p−1}$, $B^p$, $B^{p+1}$. The $p$th cohomology group consists of those elements which are cocycles but not coboundaries, that is $H^p(d) = Z^p/B^p$. This paper studies the complexity of estimating the size of $H^p(d)$ for some value of $p$.
► BibTeX data
► References
[1] Scott Aaronson. On perfect completeness for $QMA$. Quantum Information & Computation, 9 (1): 81–89, 2009. 10.48550/arXiv.0806.0450. arXiv:0806.0450.
https://doi.org/10.48550/arXiv.0806.0450
arXiv:0806.0450
[2] Scott Aaronson, Adam Bouland, Greg Kuperberg, and Saeed Mehraban. The computational complexity of ball permutations. In Proceedings of the 49th Annual ACM SIGACT Symposium on Theory of Computing, pages 317–327, 2017a. 10.1145/3055399.3055453. arXiv:1610.06646.
https://doi.org/10.1145/3055399.3055453
arXiv:1610.06646
[3] Scott Aaronson, Adam Bouland, Greg Kuperberg, and Saeed Mehraban. The computational complexity of ball permutations. In Proceedings of the 49th Annual ACM SIGACT Symposium on Theory of Computing, pages 317–327, 2017b. 10.1145/3055399.3055453. arXiv:1610.06646.
https://doi.org/10.1145/3055399.3055453
arXiv:1610.06646
[4] Michał Adamaszek and Juraj Stacho. Complexity of simplicial homology and independence complexes of chordal graphs. Computational Geometry, 57: 8 – 18, 2016. ISSN 0925-7721. https://doi.org/10.1016/j.comgeo.2016.05.003.
https://doi.org/10.1016/j.comgeo.2016.05.003
[5] Dorit Aharonov, Vaughan Jones, and Zeph Landau. A polynomial quantum algorithm for approximating the jones polynomial. Algorithmica, 55 (3): 395–421, 2009. 10.48550/arXiv.quant-ph/0511096. arXiv:quant-ph/0511096.
https://doi.org/10.48550/arXiv.quant-ph/0511096
arXiv:quant-ph/0511096
[6] Noga Alon. Eigenvalues and expanders. Combinatorica, 6 (2): 83–96, 1986. 10.1007/BF02579166.
https://doi.org/10.1007/BF02579166
[7] Robert Beals, Harry Buhrman, Richard Cleve, Michele Mosca, and Ronald de Wolf. Quantum lower bounds by polynomials. Journal of the ACM (JACM), 48 (4): 778–797, 2001. 10.1145/502090.502097. arXiv:quant-ph/9802049.
https://doi.org/10.1145/502090.502097
arXiv:quant-ph/9802049
[8] Dominic W Berry, Andrew M Childs, and Robin Kothari. Hamiltonian simulation with nearly optimal dependence on all parameters. In 2015 IEEE 56th Annual Symposium on Foundations of Computer Science, pages 792–809. IEEE, 2015. 10.1109/FOCS.2015.54. arXiv:1501.01715.
https://doi.org/10.1109/FOCS.2015.54
arXiv:1501.01715
[9] Fernando GSL Brandão. Entanglement theory and the quantum simulation of many-body physics. arXiv:0810.0026, 2008. 10.48550/arXiv.0810.0026.
https://doi.org/10.48550/arXiv.0810.0026
arXiv:0810.0026
[10] Sergey Bravyi. Efficient algorithm for a quantum analogue of 2-SAT. Contemporary Mathematics, 536: 33–48, 2011. 10.1090/conm/536/10552.
https://doi.org/10.1090/conm/536/10552
[11] Sergey B Bravyi and Alexei Yu Kitaev. Fermionic quantum computation. Annals of Physics, 298 (1): 210–226, 2002. 10.1006/aphy.2002.6254. arXiv:quant-ph/0003137.
https://doi.org/10.1006/aphy.2002.6254
arXiv:quant-ph/0003137
[12] Brielin Brown, Steven T. Flammia, and Norbert Schuch. Computational difficulty of computing the density of states. Physical Review Letters, 107 (4), Jul 2011. ISSN 1079-7114. 10.1103/physrevlett.107.040501. arXiv:1010.3060.
https://doi.org/10.1103/physrevlett.107.040501
arXiv:1010.3060
[13] Chris Cade and Ashley Montanaro. The quantum complexity of computing Schatten $p$-norms. In 13th Conference on the Theory of Quantum Computation, Communication and Cryptography, 2018. 10.4230/LIPIcs.TQC.2018.4. arXiv:1706.09279.
https://doi.org/10.4230/LIPIcs.TQC.2018.4
arXiv:1706.09279
[14] Yudong Cao, Jonathan Romero, Jonathan P Olson, Matthias Degroote, Peter D Johnson, Mária Kieferová, Ian D Kivlichan, Tim Menke, Borja Peropadre, Nicolas PD Sawaya, et al. Quantum chemistry in the age of quantum computing. Chemical reviews, 119 (19): 10856–10915, 2019. 10.1021/acs.chemrev.8b00803. arXiv:1812.09976.
https://doi.org/10.1021/acs.chemrev.8b00803
arXiv:1812.09976
[15] Henry Cartan and Samuel Eilenberg. Homological Algebra (PMS-19). Princeton University Press, 2016.
[16] Andrew M Childs, Yuan Su, Minh C Tran, Nathan Wiebe, and Shuchen Zhu. A theory of Trotter error. arXiv:1912.08854, 2019. 10.1103/PhysRevX.11.011020.
https://doi.org/10.1103/PhysRevX.11.011020
arXiv:1912.08854
[17] P. Marcos Crichigno. Supersymmetry and Quantum Computation. 11 2020.
[18] Toby Cubitt and Ashley Montanaro. Complexity classification of local Hamiltonian problems. SIAM Journal on Computing, 45 (2): 268–316, 2016. 10.1137/140998287. arXiv:1311.3161.
https://doi.org/10.1137/140998287
arXiv:1311.3161
[19] Jan de Gier, Gyorgy Z. Feher, Bernard Nienhuis, and Magdalena Rusaczonek. Integrable supersymmetric chain without particle conservation. J. Stat. Mech., 1602 (2): 023104, 2016. 10.1088/1742-5468/2016/02/023104.
https://doi.org/10.1088/1742-5468/2016/02/023104
[20] A Drucker and R de Wolf. Quantum proofs for classical theorems. Theory of Computing, 2011. 10.48550/arXiv.0910.3376. arXiv:0910.3376.
https://doi.org/10.48550/arXiv.0910.3376
arXiv:0910.3376
[21] Herbert Edelsbrunner and John L. Harer. Computational Topology: An Introduction, volume 47. 2009. 10.1007/978-3-540-33259-6_7.
https://doi.org/10.1007/978-3-540-33259-6_7
[22] Edward Farhi, Jeffrey Goldstone, and Sam Gutmann. A quantum approximate optimization algorithm. 2014. 10.48550/arXiv.1412.6062.
https://doi.org/10.48550/arXiv.1412.6062
[23] Paul Fendley and Kareljan Schoutens. Exact results for strongly correlated fermions in 2+ 1 dimensions. Physical review letters, 95 (4): 046403, 2005. 10.1103/PhysRevLett.95.046403. arXiv:cond-mat/0504595.
https://doi.org/10.1103/PhysRevLett.95.046403
arXiv:cond-mat/0504595
[24] Paul Fendley and Kareljan Schoutens. Cooper pairs and exclusion statistics from coupled free-fermion chains. J. Stat. Mech., 0702: P02017, 2007. 10.1088/1742-5468/2007/02/P02017.
https://doi.org/10.1088/1742-5468/2007/02/P02017
[25] Paul Fendley, Bernard Nienhuis, and Kareljan Schoutens. Lattice fermion models with supersymmetry. Journal of Physics A: Mathematical and General, 36 (50): 12399–12424, Dec 2003a. ISSN 1361-6447. 10.1088/0305-4470/36/50/004. arXiv:cond-mat/0307338.
https://doi.org/10.1088/0305-4470/36/50/004
arXiv:cond-mat/0307338
[26] Paul Fendley, Kareljan Schoutens, and Jan de Boer. Lattice models with $mathcal{N}=2$ supersymmetry. Physical review letters, 90 (12): 120402, 2003b. 10.1103/PhysRevLett.90.120402. arXiv:hep-th/0210161.
https://doi.org/10.1103/PhysRevLett.90.120402
arXiv:hep-th/0210161
[27] B. Foxen, C. Neill, A. Dunsworth, P. Roushan, B. Chiaro, A. Megrant, J. Kelly, Zijun Chen, K. Satzinger, and R. Barends. Demonstrating a continuous set of two-qubit gates for near-term quantum algorithms. Physical Review Letters, 125 (12), Sep 2020. ISSN 1079-7114. 10.1103/physrevlett.125.120504. arXiv:2001.08343.
https://doi.org/10.1103/physrevlett.125.120504
arXiv:2001.08343
[28] M. Freedman. $mathsf{P}/mathsf{NP}$, and the quantum field computer. Proceedings of the National Academy of Sciences of the United States of America, 95 1: 98–101, 1998. 10.1073/pnas.95.1.98.
https://doi.org/10.1073/pnas.95.1.98
[29] Michael Freedman, Alexei Kitaev, Michael Larsen, and Zhenghan Wang. Topological quantum computation. Bulletin of the American Mathematical Society, 40 (1): 31–38, 2003. arXiv:quant-ph/0101025.
arXiv:quant-ph/0101025
[30] Michael H. Freedman, Alexei Kitaev, and Zhenghan Wang. Simulation of topological field theories by quantum computers. Communications in Mathematical Physics, 227 (3): 587–603, Jun 2002a. ISSN 1432-0916. 10.1007/s002200200635. arXiv:quant-ph/0001071.
https://doi.org/10.1007/s002200200635
arXiv:quant-ph/0001071
[31] Michael H Freedman, Michael Larsen, and Zhenghan Wang. A modular functor which is universal for quantum computation. Communications in Mathematical Physics, 227 (3): 605–622, 2002b. 10.1007/s002200200645. arXiv:quant-ph/0001108.
https://doi.org/10.1007/s002200200645
arXiv:quant-ph/0001108
[32] Wenbo Fu, Davide Gaiotto, Juan Maldacena, and Subir Sachdev. Supersymmetric Sachdev-Ye-Kitaev models. Phys. Rev. D, 95 (2): 026009, 2017a. 10.1103/PhysRevD.95.026009. [Addendum: Phys.Rev.D 95, 069904 (2017)].
https://doi.org/10.1103/PhysRevD.95.026009
[33] Wenbo Fu, Davide Gaiotto, Juan Maldacena, and Subir Sachdev. Supersymmetric sachdev-ye-kitaev models. Physical Review D, 95 (6), Mar 2017b. ISSN 2470-0029. 10.1103/physrevd.95.069904.
https://doi.org/10.1103/physrevd.95.069904
[34] Sevag Gharibian, Yichen Huang, Zeph Landau, and Seung Woo Shin. Quantum Hamiltonian complexity. Theoretical Computer Science, 10 (3): 159–282, 2014. 10.1561/0400000066. arXiv:1401.3916.
https://doi.org/10.1561/0400000066
arXiv:1401.3916
[35] Robert Ghrist. Barcodes: the persistent topology of data. Bulletin of the American Mathematical Society, 45 (1): 61–75, 2008. 10.1090/S0273-0979-07-01191-3.
https://doi.org/10.1090/S0273-0979-07-01191-3
[36] Oded Goldreich. On promise problems: A survey. In Theoretical computer science, pages 254–290. Springer, 2006. 10.1007/11685654_12.
https://doi.org/10.1007/11685654_12
[37] David Gosset and Daniel Nagaj. Quantum 3-sat is $QMA_1$-complete. 2013 IEEE 54th Annual Symposium on Foundations of Computer Science, Oct 2013. 10.1109/focs.2013.86. arXiv:1302.0290.
https://doi.org/10.1109/focs.2013.86
arXiv:1302.0290
[38] Tarun Grover, D.N. Sheng, and Ashvin Vishwanath. Emergent Space-Time Supersymmetry at the Boundary of a Topological Phase. Science, 344 (6181): 280–283, 2014. 10.1126/science.1248253.
https://doi.org/10.1126/science.1248253
[39] Anna Gundert and May Szedlák. Higher dimensional cheeger inequalities. In Proceedings of the thirtieth annual symposium on Computational geometry, pages 181–188, 2014. 10.1145/2582112.2582118. arXiv:1401.2290.
https://doi.org/10.1145/2582112.2582118
arXiv:1401.2290
[40] Casper Gyurik, Chris Cade, and Vedran Dunjko. Towards quantum advantage for topological data analysis. arXiv:2005.02607, 2020. 10.22331/q-2022-11-10-855.
https://doi.org/10.22331/q-2022-11-10-855
arXiv:2005.02607
[41] Christian Hagendorf, Thessa B Fokkema, and Liza Huijse. Bethe ansatz solvability and supersymmetry of the M2 model of single fermions and pairs. Journal of Physics A: Mathematical and Theoretical, 47 (48): 485201, Nov 2014. ISSN 1751-8121. 10.1088/1751-8113/47/48/485201. arXiv:1408.4403.
https://doi.org/10.1088/1751-8113/47/48/485201
arXiv:1408.4403
[42] Danijela Horak and Jürgen Jost. Spectra of combinatorial laplace operators on simplicial complexes. Advances in Mathematics, 244: 303–336, 2013. 10.1016/j.aim.2013.05.007. arXiv:1105.2712.
https://doi.org/10.1016/j.aim.2013.05.007
arXiv:1105.2712
[43] K. Hori, S. Katz, A. Klemm, R. Pandharipande, R. Thomas, C. Vafa, R. Vakil, and E. Zaslow. Mirror symmetry, volume 1 of Clay mathematics monographs. AMS, Providence, USA, 2003. 10.1088/1126-6708/2001/07/022.
https://doi.org/10.1088/1126-6708/2001/07/022
[44] Hsin-Yuan Huang, Richard Kueng, Giacomo Torlai, Victor V. Albert, and John Preskill. Provably efficient machine learning for quantum many-body problems. 2021. 10.1126/science.abk3333.
https://doi.org/10.1126/science.abk3333
[45] L. Huijse, Dhagash Bharatbhai Mehta, N. Moran, K. Schoutens, and J. Vala. Supersymmetric lattice fermions on the triangular lattice: Superfrustration and criticality. New Journal of Physics., 14: 073002, 2012. 10.1088/1367-2630/14/7/073002.
https://doi.org/10.1088/1367-2630/14/7/073002
[46] Liza Huijse, Kareljan Schoutens, et al. Supersymmetry, lattice fermions, independence complexes and cohomology theory. Advances in Theoretical and Mathematical Physics, 14 (2): 643–694, 2010. 10.48550/arXiv.0903.0784. arXiv:0903.0784.
https://doi.org/10.48550/arXiv.0903.0784
arXiv:0903.0784
[47] Dominik Janzing and Pawel Wocjan. A simple $mathsf{PromiseBQP}$-complete matrix problem. Theory of computing, 3 (1): 61–79, 2007.
https://doi.org/10.4086/toc.2007.v003a004
[48] Jakob Jonsson. Certain homology cycles of the independence complex of grids. Discrete & Computational Geometry, 43 (4): 927–950, 2010. 10.1007/s00454-009-9224-9.
https://doi.org/10.1007/s00454-009-9224-9
[49] Georg Junker. Supersymmetric Methods in Quantum and Statistical Physics. Theoretical and Mathematical Physics. Springer-Verlag Berlin Heidelberg, 1996. 10.1007/978-3-642-61194-0.
https://doi.org/10.1007/978-3-642-61194-0
[50] Tomasz Kaczynski, Konstantin Michael Mischaikow, Marian Mrozek, and Konstantin Mischaikow. Computational homology. Applied mathematical sciences (Springer-Verlag New York Inc.); v. 157. Springer, New York, 2004. ISBN 0387408533.
[51] Volker Kaibel and Marc E. Pfetsch. Some Algorithmic Problems in Polytope Theory. arXiv Mathematics e-prints, , February 2002.
https://arxiv.org/math/0202204
[52] Julia Kempe and Oded Regev. $3$-local hamitonian is $QMA$-complete. Quantum Information & Computation, 3 (3): 258–264, 2003. arXiv:quant-ph/0302079.
arXiv:quant-ph/0302079
[53] Julia Kempe, Alexei Kitaev, and Oded Regev. The complexity of the local Hamiltonian problem. SIAM Journal on Computing, 35 (5): 1070–1097, 2006. 10.1137/S0097539704445226. arXiv:quant-ph/0406180.
https://doi.org/10.1137/S0097539704445226
arXiv:quant-ph/0406180
[54] A. Yu. Kitaev, A. H. Shen, and M. N. Vyalyi. Classical and Quantum Computation. Graduate Studies in Mathematics, 2002.
[55] A.Yu. Kitaev. Fault-tolerant quantum computation by anyons. Annals of Physics, 303 (1): 2–30, Jan 2003. ISSN 0003-4916. 10.1016/s0003-4916(02)00018-0. arXiv:quant-ph/9707021.
https://doi.org/10.1016/s0003-4916(02)00018-0
arXiv:quant-ph/9707021
[56] Ville Lahtinen and Jiannis Pachos. A short introduction to topological quantum computation. SciPost Physics, 3 (3), Sep 2017. ISSN 2542-4653. 10.21468/scipostphys.3.3.021. arXiv:1705.04103.
https://doi.org/10.21468/scipostphys.3.3.021
arXiv:1705.04103
[57] James PF LeBlanc, Andrey E Antipov, Federico Becca, Ireneusz W Bulik, Garnet Kin-Lic Chan, Chia-Min Chung, Youjin Deng, Michel Ferrero, Thomas M Henderson, Carlos A Jiménez-Hoyos, et al. Solutions of the two-dimensional hubbard model: Benchmarks and results from a wide range of numerical algorithms. Physical Review X, 5 (4): 041041, 2015. 10.1103/PhysRevX.5.041041. arXiv:1505.02290.
https://doi.org/10.1103/PhysRevX.5.041041
arXiv:1505.02290
[58] James R Lee, Shayan Oveis Gharan, and Luca Trevisan. Multiway spectral partitioning and higher-order cheeger inequalities. Journal of the ACM (JACM), 61 (6): 1–30, 2014. 10.1145/2665063. arXiv:1111.1055.
https://doi.org/10.1145/2665063
arXiv:1111.1055
[59] Yi-Kai Liu, Matthias Christandl, and F. Verstraete. Quantum computational complexity of the $n$-representability problem: $QMA$ complete. Physical Review Letters, 98 (11), Mar 2007. ISSN 1079-7114. 10.1103/physrevlett.98.110503. arXiv:quant-ph/0609125.
https://doi.org/10.1103/physrevlett.98.110503
arXiv:quant-ph/0609125
[60] Seth Lloyd. Universal quantum simulators. Science, pages 1073–1078, 1996. science.273.5278.1073. arXiv:quant-ph/9703054.
arXiv:quant-ph/9703054
[61] Seth Lloyd, Silvano Garnerone, and Paolo Zanardi. Quantum algorithms for topological and geometric analysis of data. Nature Communications, 7 (1): 10138, 2016. 10.1038/ncomms10138. arXiv:1408.3106.
https://doi.org/10.1038/ncomms10138
arXiv:1408.3106
[62] Jarrod R McClean, Jonathan Romero, Ryan Babbush, and Alán Aspuru-Guzik. The theory of variational hybrid quantum-classical algorithms. New Journal of Physics, 18 (2): 023023, 2016. 10.1088/1367-2630/18/2/023023. arXiv:1509.04279.
https://doi.org/10.1088/1367-2630/18/2/023023
arXiv:1509.04279
[63] Jarrod R McClean, Nicholas C Rubin, Joonho Lee, Matthew P Harrigan, Thomas E O’Brien, Ryan Babbush, William J Huggins, and Hsin-Yuan Huang. What the foundations of quantum computer science teach us about chemistry. arXiv:2106.03997, 2021. 10.1063/5.0060367.
https://doi.org/10.1063/5.0060367
arXiv:2106.03997
[64] Jiří Minář, Bart van Voorden, and Kareljan Schoutens. Kink dynamics and quantum simulation of supersymmetric lattice Hamiltonians. arXiv:2005.00607, 2020.
arXiv:2005.00607
[65] Tomoyuki Morimae, Keisuke Fujii, and Joseph F Fitzsimons. Hardness of classically simulating the one-clean-qubit model. Physical review letters, 112 (13): 130502, 2014. 10.1103/PhysRevLett.112.130502. arXiv:1312.2496.
https://doi.org/10.1103/PhysRevLett.112.130502
arXiv:1312.2496
[66] H. Nicolai. Supersymmetry and Spin Systems. Journal of Physics A, 9: 1497–1506, 1976. 10.1088/0305-4470/9/9/010.
https://doi.org/10.1088/0305-4470/9/9/010
[67] Bryan O’Gorman, Sandy Irani, James Whitfield, and Bill Fefferman. Electronic structure in a fixed basis is qma-complete. arXiv:2103.08215, 2021. 10.48550/arXiv.2103.08215.
https://doi.org/10.48550/arXiv.2103.08215
arXiv:2103.08215
[68] Sourabh Palande and Bei Wang. Spectral sparsification of simplicial complexes for clustering and label propagation. Journal of Computational Geometry, 11 (1): 176–211, 2020. 10.20382/jocg.v11i1a8. arXiv:1708.08436.
https://doi.org/10.20382/jocg.v11i1a8
arXiv:1708.08436
[69] Ori Parzanchevski, Ron Rosenthal, and Ran J Tessler. Isoperimetric inequalities in simplicial complexes. Combinatorica, 36 (2): 195–227, 2016. 10.1007/s00493-014-3002-x. arXiv:1207.0638.
https://doi.org/10.1007/s00493-014-3002-x
arXiv:1207.0638
[70] Richard Peng, He Sun, and Luca Zanetti. Partitioning well-clustered graphs: Spectral clustering works! In Conference on Learning Theory, pages 1423–1455. PMLR, 2015. 10.1137/15M1047209. arXiv:1411.2021.
https://doi.org/10.1137/15M1047209
arXiv:1411.2021
[71] Alberto Peruzzo, Jarrod McClean, Peter Shadbolt, Man-Hong Yung, Xiao-Qi Zhou, Peter J Love, Alán Aspuru-Guzik, and Jeremy L O’brien. A variational eigenvalue solver on a photonic quantum processor. Nature communications, 5 (1): 1–7, 2014. 10.1038/ncomms5213. arXiv:1304.3061.
https://doi.org/10.1038/ncomms5213
arXiv:1304.3061
[72] John Preskill. Lecture notes for Physics 219: Quantum computation. Caltech Lecture Notes, 1999. Link.
http://www.theory.caltech.edu/preskill/ph219/topological.pdf
[73] Armin Rahmani, Xiaoyu Zhu, Marcel Franz, and Ian Affleck. Emergent Supersymmetry from Strongly Interacting Majorana Zero Modes. prl, 115 (16): 166401, October 2015. 10.1103/PhysRevLett.115.166401.
https://doi.org/10.1103/PhysRevLett.115.166401
[74] Christian Reiher. The clique density theorem. Annals of Mathematics, pages 683–707, 2016. 10.48550/arXiv.1212.2454. arXiv:1212.2454.
https://doi.org/10.48550/arXiv.1212.2454
arXiv:1212.2454
[75] Burak Sahinoglu and Rolando Somma. Hamiltonian simulation in the low energy subspace. Bulletin of the American Physical Society. 10.1038/s41534-021-00451-w. arXiv:2006.02660.
https://doi.org/10.1038/s41534-021-00451-w
arXiv:2006.02660
[76] Hubert Saleur and Nicholas P Warner. Lattice models and n= 2 supersymmetry. In Quantum Field Theory and String Theory, pages 335–377. Springer, 1995. arXiv:hep-th/9311138.
arXiv:hep-th/9311138
[77] Raoul Santachiara and Kareljan Schoutens. Supersymmetric model of spin-1/2 fermions on a chain. Journal of Physics A Mathematical General, 38 (24): 5425–5439, June 2005. 10.1088/0305-4470/38/24/003.
https://doi.org/10.1088/0305-4470/38/24/003
[78] Peter Scheiblechner. On the complexity of deciding connectedness and computing betti numbers of a complex algebraic variety. Journal of Complexity, 23 (3): 359–379, 2007. 10.1016/j.jco.2007.03.008.
https://doi.org/10.1016/j.jco.2007.03.008
[79] Jacob T Seeley, Martin J Richard, and Peter J Love. The Bravyi-Kitaev transformation for quantum computation of electronic structure. The Journal of chemical physics, 137 (22): 224109, 2012. 10.1063/1.4768229. arXiv:1208.5986.
https://doi.org/10.1063/1.4768229
arXiv:1208.5986
[80] Peter W. Shor. Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer. SIAM Journal on Computing, 26 (5): 1484–1509, Oct 1997. ISSN 1095-7111. 10.1137/s0097539795293172. arXiv:quant-ph/9508027.
https://doi.org/10.1137/s0097539795293172
arXiv:quant-ph/9508027
[81] John Steenbergen, Caroline Klivans, and Sayan Mukherjee. A cheeger-type inequality on simplicial complexes. Advances in Applied Mathematics, 56: 56–77, 2014. 10.1016/j.aam.2014.01.002. arXiv:1209.5091.
https://doi.org/10.1016/j.aam.2014.01.002
arXiv:1209.5091
[82] Hendrik van Eerten. Extensive ground state entropy in supersymmetric lattice models. Journal of mathematical physics, 46 (12): 123302, 2005. 10.1063/1.2142836. arXiv:cond-mat/0509581.
https://doi.org/10.1063/1.2142836
arXiv:cond-mat/0509581
[83] Larry Wasserman. Topological data analysis. Annual Review of Statistics and Its Application, 5: 501–532, 2018. 10.1146/annurev-statistics-031017-100045. arXiv:1609.08227.
https://doi.org/10.1146/annurev-statistics-031017-100045
arXiv:1609.08227
[84] John Watrous. Quantum Computational Complexity, pages 7174–7201. Springer New York, New York, NY, 2009. ISBN 978-0-387-30440-3. 10.1007/978-0-387-30440-3_428. quant-ph/0804.3401.
https://doi.org/10.1007/978-0-387-30440-3_428
arXiv:0804.3401
[85] Charles A. Weibel. An Introduction to Homological Algebra. Cambridge Studies in Advanced Mathematics. Cambridge University Press, 1994. 10.1017/CBO9781139644136.
https://doi.org/10.1017/CBO9781139644136
[86] Charles A. Weibel. Chapter 28 – History of Homological Algebra. In I.M. James, editor, History of Topology, pages 797–836. North-Holland, Amsterdam, 1999. ISBN 978-0-444-82375-5. https://doi.org/10.1016/B978-044482375-5/50029-8.
https://doi.org/10.1016/B978-044482375-5/50029-8
[87] Edward Witten. Dynamical Breaking of Supersymmetry. Nuclear Physics B, 188: 513, 1981. 10.1016/0550-3213(81)90006-7.
https://doi.org/10.1016/0550-3213(81)90006-7
[88] Edward Witten. Constraints on Supersymmetry Breaking. Nuclear Physics B, 202: 253, 1982a. 10.1016/0550-3213(82)90071-2.
https://doi.org/10.1016/0550-3213(82)90071-2
[89] Edward Witten. Supersymmetry and Morse theory. J. Differential Geometry, 17 (4): 661–692, 1982b. 10.4310/jdg/1214437492.
https://doi.org/10.4310/jdg/1214437492
[90] Edward Witten. Quantum Field Theory and the Jones Polynomial. Communications in Mathematical Physics, 121: 351–399, 1989. 10.1007/BF01217730.
https://doi.org/10.1007/BF01217730
[91] Xiao Yang and Paul Fendley. Non-local spacetime supersymmetry on the lattice. Journal of Physics A Mathematical General, 37 (38): 8937–8948, September 2004. 10.1088/0305-4470/37/38/003.
https://doi.org/10.1088/0305-4470/37/38/003
[92] Afra J. Zomorodian. Topology for Computing. Cambridge Monographs on Applied and Computational Mathematics. Cambridge University Press, 2005. 10.1017/CBO9780511546945.
https://doi.org/10.1017/CBO9780511546945
Cited by
[1] Alexander M. Dalzell, Sam McArdle, Mario Berta, Przemyslaw Bienias, Chi-Fang Chen, András Gilyén, Connor T. Hann, Michael J. Kastoryano, Emil T. Khabiboulline, Aleksander Kubica, Grant Salton, Samson Wang, and Fernando G. S. L. Brandão, “Quantum algorithms: A survey of applications and end-to-end complexities”, arXiv:2310.03011, (2023).
[2] Ismail Yunus Akhalwaya, Shashanka Ubaru, Kenneth L. Clarkson, Mark S. Squillante, Vishnu Jejjala, Yang-Hui He, Kugendran Naidoo, Vasileios Kalantzis, and Lior Horesh, “Topological data analysis on noisy quantum computers”, arXiv:2209.09371, (2022).
[3] Dominic W. Berry, Yuan Su, Casper Gyurik, Robbie King, Joao Basso, Alexander Del Toro Barba, Abhishek Rajput, Nathan Wiebe, Vedran Dunjko, and Ryan Babbush, “Analyzing Prospects for Quantum Advantage in Topological Data Analysis”, PRX Quantum 5 1, 010319 (2024).
[4] Alexander Schmidhuber and Seth Lloyd, “Complexity-Theoretic Limitations on Quantum Algorithms for Topological Data Analysis”, PRX Quantum 4 4, 040349 (2023).
[5] Sam McArdle, András Gilyén, and Mario Berta, “A streamlined quantum algorithm for topological data analysis with exponentially fewer qubits”, arXiv:2209.12887, (2022).
[6] Sergey Bravyi, Anirban Chowdhury, David Gosset, Vojtěch Havlíček, and Guanyu Zhu, “Quantum Complexity of the Kronecker Coefficients”, PRX Quantum 5 1, 010329 (2024).
[7] Casper Gyurik, Chris Cade, and Vedran Dunjko, “Towards quantum advantage via topological data analysis”, arXiv:2005.02607, (2020).
[8] Ismail Yunus Akhalwaya, Yang-Hui He, Lior Horesh, Vishnu Jejjala, William Kirby, Kugendran Naidoo, and Shashanka Ubaru, “Representation of the Fermionic Boundary Operator”, arXiv:2201.11510, (2022).
[9] Casper Gyurik and Vedran Dunjko, “Exponential separations between classical and quantum learners”, arXiv:2306.16028, (2023).
[10] Simon Apers, Sander Gribling, Sayantan Sen, and Dániel Szabó, “A (simple) classical algorithm for estimating Betti numbers”, Quantum 7, 1202 (2023).
[11] Marcos Crichigno and Tamara Kohler, “Clique Homology is QMA1-hard”, arXiv:2209.11793, (2022).
[12] Sevag Gharibian, “The 7 faces of quantum NP”, arXiv:2310.18010, (2023).
[13] Casper Gyurik, Chris Cade, and Vedran Dunjko, “Towards quantum advantage via topological data analysis”, Quantum 6, 855 (2022).
[14] Robbie King and Tamara Kohler, “Promise Clique Homology on weighted graphs is $text{QMA}_1$-hard and contained in $text{QMA}$”, arXiv:2311.17234, (2023).
[15] Ismail Yunus Akhalwaya, Yang-Hui He, Lior Horesh, Vishnu Jejjala, William Kirby, Kugendran Naidoo, and Shashanka Ubaru, “Representation of the fermionic boundary operator”, Physical Review A 106 2, 022407 (2022).
[16] Stefano Scali, Chukwudubem Umeano, and Oleksandr Kyriienko, “The topology of data hides in quantum thermal states”, arXiv:2402.15633, (2024).
[17] Roberto Zucchini, “A new quantum computational set-up for algebraic topology via simplicial sets”, arXiv:2309.11304, (2023).
[18] Nhat A. Nghiem, “Alternative Method for Estimating Betti Numbers”, arXiv:2403.04686, (2024).
[19] Ryu Hayakawa, Kuo-Chin Chen, and Min-Hsiu Hsieh, “Quantum Walks on Simplicial Complexes and Harmonic Homology: Application to Topological Data Analysis with Superpolynomial Speedups”, arXiv:2404.15407, (2024).
The above citations are from SAO/NASA ADS (last updated successfully 2024-05-01 15:31:16). The list may be incomplete as not all publishers provide suitable and complete citation data.
On Crossref’s cited-by service no data on citing works was found (last attempt 2024-05-01 15:31:14).
This Paper is published in Quantum under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. Copyright remains with the original copyright holders such as the authors or their institutions.
- SEO Powered Content & PR Distribution. Get Amplified Today.
- PlatoData.Network Vertical Generative Ai. Empower Yourself. Access Here.
- PlatoAiStream. Web3 Intelligence. Knowledge Amplified. Access Here.
- PlatoESG. Carbon, CleanTech, Energy, Environment, Solar, Waste Management. Access Here.
- PlatoHealth. Biotech and Clinical Trials Intelligence. Access Here.
- Source: https://quantum-journal.org/papers/q-2024-04-30-1325/
- :is
- :not
- ][p
- 003
- 01
- 02
- 05
- 1
- 10
- 1010
- 107
- 11
- 12
- 121
- 125
- 13
- 14
- 15%
- 16
- 17
- 19
- 1981
- 1994
- 1995
- 1996
- 1998
- 1999
- 2%
- 20
- 2001
- 2005
- 2006
- 2007
- 2008
- 2009
- 2010
- 2011
- 2012
- 2013
- 2014
- 2015
- 2016
- 2017
- 2018
- 2019
- 202
- 2020
- 2021
- 2022
- 2023
- 2024
- 21
- 22
- 23
- 24
- 25
- 253
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35%
- 36
- 39
- 4
- 40
- 41
- 42
- 45
- 46
- 48
- 49
- 5
- 50
- 51
- 52
- 54
- 55
- 58
- 6
- 60
- 62
- 65
- 66
- 67
- 7
- 70
- 72
- 73
- 74
- 75
- 77
- 8
- 80
- 84
- 87
- 89
- 9
- 90
- 91
- 98
- a
- About
- above
- ABSTRACT
- Academy
- access
- ACM
- Adam
- advanced
- advances
- ADvantage
- affiliations
- age
- aim
- AL
- Alexander
- algebra
- algebraic
- algorithm
- algorithmic
- algorithms
- All
- alternative
- america
- American
- amsterdam
- an
- analogue
- analysis
- analyzing
- and
- Andrew
- anna
- annual
- Application
- applications
- applied
- approximate
- apr
- ARE
- argue
- arise
- AS
- At
- attempt
- author
- authors
- b
- ball
- bart
- basis
- BE
- benchmarks
- berlin
- berry
- between
- Bill
- bounds
- Break
- Breaking
- Bringing
- brown
- Bryan
- bulletin
- but
- by
- cambridge
- cao
- carlos
- caroline
- casper
- certain
- chain
- chains
- chan
- Chapter
- Charles
- chemical
- chemistry
- chen
- Chris
- christian
- citing
- class
- classification
- clique
- clustering
- coefficients
- College
- comment
- Commons
- Communication
- Communications
- complete
- completeness
- complex
- complexes
- complexities
- complexity
- computation
- computational
- computer
- computer science
- computers
- computing
- Conference
- CONSERVATION
- Consider
- Consisting
- consists
- constraints
- contained
- contemporary
- context
- continuous
- cooper
- copyright
- correlated
- coupled
- criticality
- cryptography
- CWI
- cycles
- Daniel
- data
- data analysis
- David
- de
- Deciding
- del
- demonstrating
- Den
- density
- dependence
- detail
- Difficulty
- dimensions
- direction
- discrete
- discuss
- dominic
- Door
- dynamics
- e
- E&T
- editor
- Edward
- efficient
- Electronic
- elements
- emil
- end-to-end
- energy
- entanglement
- error
- Ether (ETH)
- exact
- exactly
- existing
- exponential
- exponentially
- extensive
- faces
- fact
- February
- Federico
- fewer
- field
- finding
- First
- first steps
- fixed
- For
- found
- Foundations
- FRAME
- freedman
- from
- fu
- Gates
- General
- geometry
- graduate
- grant
- graph
- graphs
- greg
- Ground
- Group
- Hard
- hardness
- harvard
- he
- henry
- High
- higher
- history
- holders
- Holes
- http
- HTTPS
- huang
- Hybrid
- hybrid quantum-classical
- i
- IEEE
- if
- image
- Imperial
- Imperial College
- in
- Inc.
- Including
- independence
- inequalities
- Inequality
- information
- instances
- institutions
- interacting
- interesting
- International
- introducing
- Introduction
- IT
- ITS
- jacob
- james
- Jan
- JavaScript
- jeffrey
- jeremy
- John
- Johnson
- jonathan
- jones
- journal
- juan
- julia
- june
- kenneth
- King
- kirby
- Label
- laboratory
- large
- Last
- learners
- learning
- Leave
- Lecture
- Lee
- License
- light
- limitations
- LINK
- List
- local
- logarithms
- London
- love
- Low
- lower
- M2
- machine
- machine learning
- Main
- many
- mar
- Mario
- mark
- Martin
- mathematical
- mathematics
- Matrix
- matthew
- matthias
- max-width
- May..
- mcclean
- method
- methods
- Michael
- mirror
- model
- models
- modes
- modular
- Month
- Motivation
- Mukherjee
- nathan
- National
- Natural
- Nature
- nearly
- Netherlands
- New
- New York
- nicholas
- Nicolas
- no
- nontrivial
- Notes
- nov
- nuclear
- Nuclear physics
- number
- numbers
- numerical
- NY
- Oct
- october
- of
- Offers
- on
- ones
- only
- open
- opens
- operator
- operators
- optimal
- optimization
- or
- original
- our
- pages
- pairs
- Paolo
- Paper
- parameters
- particle
- Paul
- perfect
- perspective
- Peter
- phase
- physical
- Physics
- plato
- Plato Data Intelligence
- PlatoData
- polynomial
- polynomials
- press
- Prime
- Prince
- princeton
- Problem
- problems
- Proceedings
- Processor
- promise
- proofs
- propagation
- prospects
- provably
- provide
- published
- publisher
- publishers
- Quantum
- quantum advantage
- quantum algorithms
- Quantum Computer
- quantum computers
- quantum computing
- quantum information
- qubits
- R
- ran
- range
- references
- relationship
- remains
- representation
- Results
- review
- Reviews
- Richard
- robbie
- ROBERT
- roberto
- Robin
- RON
- Ryan
- s
- Sam
- sandy
- Science
- SCIENCES
- scott
- scott aaronson
- September
- set
- Sets
- Short
- show
- showing
- siam
- Simon
- Simple
- simulation
- single
- Size
- Society
- Solutions
- some
- Spectral
- Spin
- State
- States
- statistical
- statistics
- Steps
- steven
- streamlined
- String
- strongly
- structure
- studies
- Study
- Studying
- Successfully
- such
- Suggests
- suitable
- Sun
- Survey
- symmetry
- Symposium
- system
- Systems
- T
- Take
- tamara
- Tarun
- terms
- th
- that
- The
- The Graph
- the Netherlands
- The United States of America
- their
- then
- theorem
- theoretical
- theory
- thermal
- These
- this
- thomas
- those
- Tim
- Title
- to
- tools
- topological quantum
- towards
- Transformation
- under
- United
- United States
- UNITED STATES OF AMERICA
- Universal
- university
- updated
- URL
- us
- USA
- value
- van
- variety
- via
- volume
- W
- walks
- wang
- want
- Warner
- was
- we
- well-known
- What
- which
- whose
- wide
- Wide range
- william
- with
- without
- Wolf
- Woo
- works
- X
- xiao
- year
- york
- Yuan
- yunus
- zephyrnet
- zero