Minimal-noise Estimation Of Noncommuting Rotations Of A Spin

Republished By Plato

Followers: 0

Jakub Czartowski^1,2, Karol Życzkowski^2,3,4, and Daniel Braun⁵

¹Doctoral School of Exact and Natural Sciences, Jagiellonian University, ul. Łojasiewicza 11, 30-348 Kraków, Poland
²Faculty of Physics, Astronomy and Applied Computer Science, Jagiellonian University, ul. Łojasiewicza 11, 30-348 Kraków, Poland
³Centrum Fizyki Teoretycznej PAN, Al. Lotników 32/46, 02-668 Warszawa, Poland
⁴National Quantum Information Center (KCIK), University of Gdańsk, Poland
⁵Institute of Theoretical Physics, University of Tübingen, Auf der Morgenstelle 14, 72076 Tübingen, Germany

Find this paper interesting or want to discuss? Scite or leave a comment on SciRate.

Abstract

We propose an analogue of $text{SU}(1,1)$ interferometry to measure rotation of a spin by using two-spin squeezed states. Attainability of the Heisenberg limit for the estimation of the rotation angle is demonstrated for maximal squeezing. For a specific direction and strength an advantage in sensitivity for $all$ equatorial rotation axes (and hence non-commuting rotations) over the classical bound is shown in terms of quadratic scaling of the single-parameter quantum Fisher information for the corresponding rotation angles. Our results provide a method for measuring magnetic fields in any direction in the $x$-$y$-plane with the same optimized initial state.

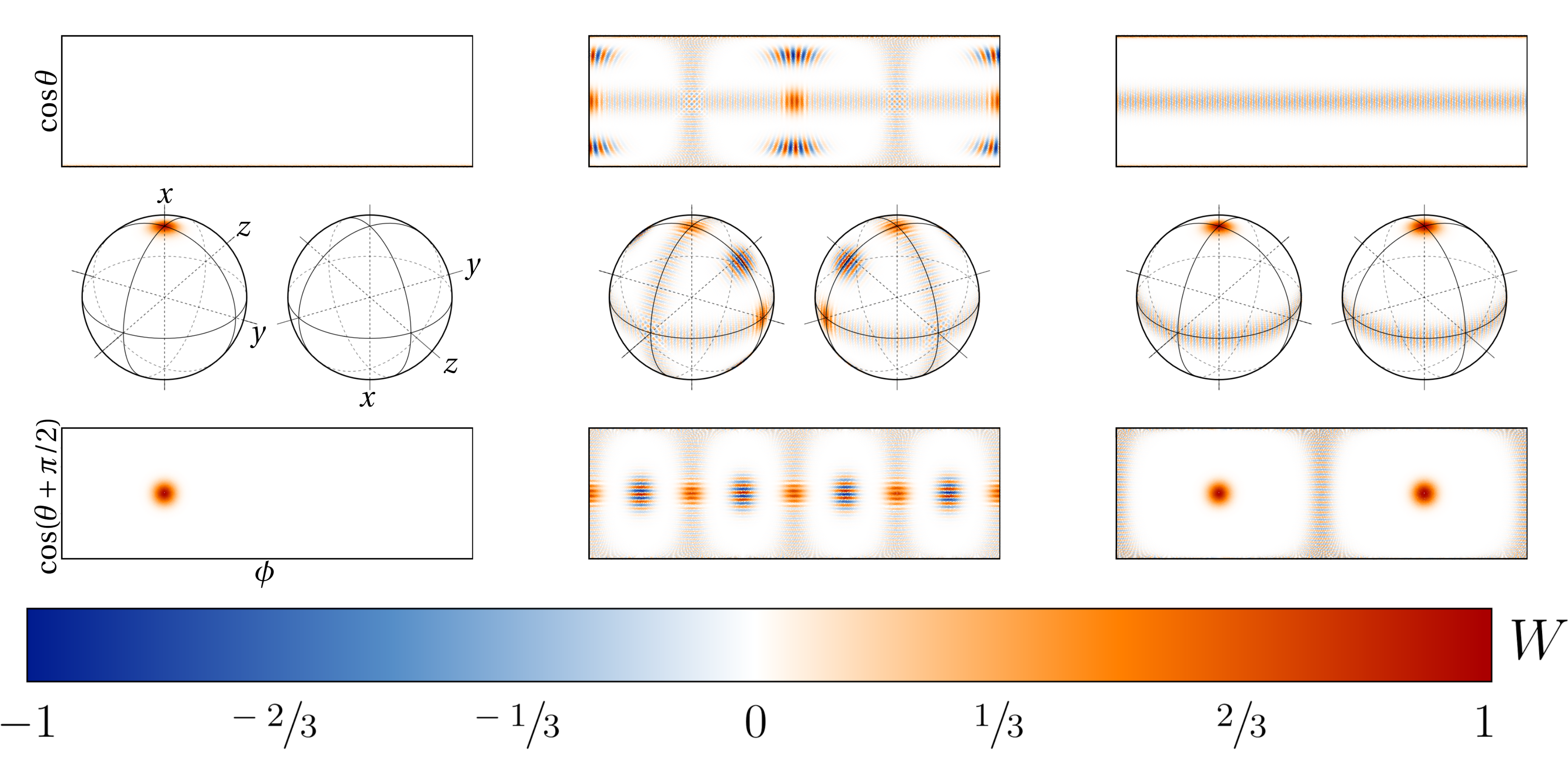
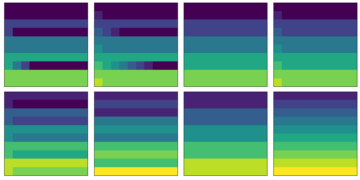
Featured image: Wigner functions $W(theta,phi)$ on the Bloch sphere for three exemplary metrologically advantageous spin states with spin $S=40$. Blue color corresponds to negative values of $W$.

Popular summary

Interferometric methods in their varied spectrum of flavours have long stood as a hallmark of physics, offering a window into phenomena such as the elusive gravitational waves. Recent developments in the understanding of $text{SU}(1,1)$ interferometry in terms of a Squeeze-Displace-Unsqueeze protocol, which depends heavily on squeezed states of light, promise novel approaches to search for dark matter. In parallel, spin squeezing has been investigated since 1971, finding its use for Bose-Einstein condensates, quantum rotosensors and other problems. In this work the ideas from both fields are merged by introducing Squeeze-Rotate-Unsqueeze protocol for single-axis squeezed spin systems. We demonstrate its advantage and adaptability from the vantage point of Quantum Fisher Information, offering a novel theoretical tool useful for sensing of magnetic fields or rotations in the polarization space.

► BibTeX data

@article{Czartowski2024minimalnoise, doi = {10.22331/q-2024-05-08-1341}, url = {https://doi.org/10.22331/q-2024-05-08-1341}, title = {Minimal-noise estimation of noncommuting rotations of a spin}, author = {Czartowski, Jakub and {.{Z}}yczkowski, Karol and Braun, Daniel}, journal = {{Quantum}}, issn = {2521-327X}, publisher = {{Verein zur F{“{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}}, volume = {8}, pages = {1341}, month = may, year = {2024} }

► References

[1] R. Demkowicz-Dobrzański, K. Banaszek, and R. Schnabel. “Fundamental quantum interferometry bound for the squeezed-light-enhanced gravitational wave detector GEO 600”. Phys. Rev. A 88, 041802 (2013).
https://doi.org/10.1103/PhysRevA.88.041802

[2] J. Aasi et al. “Enhanced sensitivity of the LIGO gravitational wave detector by using squeezed states of light”. Nature Photonics (2013).
https://doi.org/10.1038/nphoton.2013.177

[3] I. G. Irastorza and J. Redondo. “New experimental approaches in the search for axion-like particles”. Prog. Part. Nucl. Phys. 102, 89–159 (2018).
https://doi.org/10.1016/j.ppnp.2018.05.003

[4] S. C. Burd, R. Srinivas, J. J. Bollinger, A. C. Wilson, D. J. Wineland, D. Leibfried, D. H. Slichter, and D. T. C. Allcock. “Quantum amplification of mechanical oscillator motion”. Science 364, 1163–1165 (2019).
https://doi.org/10.1126/science.aaw2884

[5] B. Yurke, S. L. McCall, and J. R. Klauder. “SU(2) and SU(1,1) interferometers”. Phys. Rev. A 33, 4033–4054 (1986).
https://doi.org/10.1103/PhysRevA.33.4033

[6] C. M. Caves. “Reframing SU(1,1) interferometry”. Adv. Quantum Technol. 3, 1900138 (2020).
https://doi.org/10.1002/qute.201900138

[7] M. Tsang and C. M. Caves. “Evading quantum mechanics: Engineering a classical subsystem within a quantum environment”. Phys. Rev. X 2, 031016 (2012).
https://doi.org/10.1103/PhysRevX.2.031016

[8] G. Agarwal. “Quantum optics”. Quantum Optics. Cambridge University Press. (2013).

[9] N. Bergeal, F. Schackert, M. Metcalfe, R. Vijay, V. E. Manucharyan, L. Frunzio, D. E. Prober, R. J. Schoelkopf, S. M. Girvin, and M. H. Devoret. “Phase-preserving amplification near the quantum limit with a Josephson ring modulator”. Nature 465, 64–68 (2010).
https://doi.org/10.1038/nature09035

[10] A. Roy and M. Devoret. “Quantum-limited parametric amplification with Josephson circuits in the regime of pump depletion”. Phys. Rev. B 98, 045405 (2018).
https://doi.org/10.1103/PhysRevB.98.045405

[11] R. Vijay, D. H. Slichter, and I. Siddiqi. “Observation of quantum jumps in a superconducting artificial atom”. Phys. Rev. Lett. 106, 110502 (2011).
https://doi.org/10.1103/PhysRevLett.106.110502

[12] M. Renger, S. Pogorzalek, Q. Chen, Y. Nojiri, K. Inomata, Y. Nakamura, M. Partanen, A. Marx, R. Gross, F. Deppe, and K. G. Fedorov. “Beyond the standard quantum limit for parametric amplification of broadband signals”. npj Quantum Inf. 7, 1–7 (2021).
https://doi.org/10.1038/s41534-021-00495-y

[13] C. F. Ockeloen-Korppi, E. Damskägg, J.-M. Pirkkalainen, T. T. Heikkilä, F. Massel, and M. A. Sillanpää. “Noiseless quantum measurement and squeezing of microwave fields utilizing mechanical vibrations”. Phys. Rev. Lett. 118, 103601 (2017).
https://doi.org/10.1103/PhysRevLett.118.103601

[14] P. Sikivie. “Experimental tests of the “invisible” axion”. Phys. Rev. Lett. 51, 1415–1417 (1983).
https://doi.org/10.1103/PhysRevLett.51.1415

[15] H. Zheng, M. Silveri, R. T. Brierley, S. M. Girvin, and K. W. Lehnert. “Accelerating dark-matter axion searches with quantum measurement technology” (2016). arXiv:1607.02529.
arXiv:1607.02529

[16] M. Kitagawa and M. Ueda. “Squeezed spin states”. Phys. Rev. A 47, 5138–5143 (1993).
https://doi.org/10.1103/PhysRevA.47.5138

[17] T. Byrnes. “Fractality and macroscopic entanglement in two-component Bose-Einstein condensates”. Phys. Rev. A 88, 023609 (2013).
https://doi.org/10.1103/PhysRevA.88.023609

[18] H. Kurkjian, K. Pawłowski, A. Sinatra, and P. Treutlein. “Spin squeezing and Einstein-Podolsky-Rosen entanglement of two bimodal condensates in state-dependent potentials”. Phys. Rev. A 88, 043605 (2013).
https://doi.org/10.1103/PhysRevA.88.043605

[19] A. Sinatra, J.-C. Dornstetter, and Y. Castin. “Spin squeezing in Bose-Einstein condensates: Limits imposed by decoherence and non-zero temperature”. Front. Phys. 7, 86–97 (2011).
https://doi.org/10.1007/s11467-011-0219-7

[20] R. Corgier, N. Gaaloul, A. Smerzi, and L. Pezzè. “Delta-kick squeezing”. Phys. Rev. Lett. 127, 183401 (2021).
https://doi.org/10.1103/PhysRevLett.127.183401

[21] T. Bilitewski, L. De Marco, J.-R. Li, K. Matsuda, W. G. Tobias, G. Valtolina, J. Ye, and A. M. Rey. “Dynamical generation of spin squeezing in ultracold dipolar molecules”. Phys. Rev. Lett. 126, 113401 (2021).
https://doi.org/10.1103/PhysRevLett.126.113401

[22] D. Leibfried, M. D. Barrett, T. Schaetz, J. Britton, J. Chiaverini, W. M. Itano, J. D. Jost, C. Langer, and D. J. Wineland. “Toward Heisenberg-limited spectroscopy with multiparticle entangled states”. Science 304, 1476–1478 (2004).
https://doi.org/10.1126/science.1097576

[23] C. Chryssomalakos, L. Hanotel, E. Guzmán-González, D. Braun, E. Serrano-Ensástiga, and K. Życzkowski. “Symmetric multiqudit states: Stars, entanglement, and rotosensors”. Phys. Rev. A 104, 012407 (2021).
https://doi.org/10.1103/PhysRevA.104.012407

[24] R. Kaubruegger, P. Silvi, C. Kokail, R. van Bijnen, A. M. Rey, J. Ye, A. M. Kaufman, and P. Zoller. “Variational spin-squeezing algorithms on programmable quantum sensors”. Phys. Rev. Lett. 123, 260505 (2019).
https://doi.org/10.1103/PhysRevLett.123.260505

[25] M. F. Riedel, P. Böhi, Y. Li, T. W. Hänsch, A. Sinatra, and P. Treutlein. “Atom-chip-based generation of entanglement for quantum metrology”. Nature (2010).
https://doi.org/10.1038/nature08988

[26] S. Colombo, E. Pedrozo-Peñafiel, A. F. Adiyatullin na nAff, Z. Li, E. Mendez, C. Shu, and V. Vuletić. “Time-reversal-based quantum metrology with many-body entangled states”. Nature Physics (2022).
https://doi.org/10.1038/s41567-022-01653-5

[27] R. Kaubruegger, A. Shankar, D. V. Vasilyev, and P. Zoller. “Optimal and variational multi-parameter quantum metrology and vector field sensing”.
https://doi.org/10.1103/PRXQuantum.4.020333

[28] J. M. Radcliffe. “Some properties of coherent spin states”. J. Phys. A: Gen. Phys. 4, 313–323 (1971).
https://doi.org/10.1088/0305-4470/4/3/009

[29] F. T. Arecchi, E. Courtens, R. Gilmore, and H. Thomas. “Atomic coherent states in quantum optics”. Phys. Rev. A 6, 2211–2237 (1972).
https://doi.org/10.1103/PhysRevA.6.2211

[30] R. Holtz and J. Hanus. “On coherent spin states”. J. Phys. A: Math. Nucl. Gen. 7, L37–L40 (1974).
https://doi.org/10.1088/0305-4470/7/4/001

[31] W.-M. Zhang, D. H. Feng, and R. Gilmore. “Coherent states: Theory and some applications”. Rev. Mod. Phys. 62, 867–927 (1990).
https://doi.org/10.1103/RevModPhys.62.867

[32] G. S. Agarwal. “Relation between atomic coherent-state representation, state multipoles, and generalized phase-space distributions”. Phys. Rev. A 24, 2889–2896 (1981).
https://doi.org/10.1103/PhysRevA.24.2889

[33] J. P. Dowling, G. S. Agarwal, and W. P. Schleich. “Wigner distribution of a general angular-momentum state: Applications to a collection of two-level atoms”. Phys. Rev. A 49, 4101–4109 (1994).
https://doi.org/10.1103/PhysRevA.49.4101

[34] J. Davis, M. Kumari, R. B. Mann, and S. Ghose. “Wigner negativity in spin-$j$ systems”. Phys. Rev. Research 3, 033134 (2021).
https://doi.org/10.1103/PhysRevResearch.3.033134

[35] A. Kenfack and K. Życzkowski. “Negativity of the Wigner function as an indicator of non-classicality”. J. Opt., B Quantum semiclass. 6, 396 (2004).
https://doi.org/10.1088/1464-4266/6/10/003

[36] J. Kitzinger, M. Chaudhary, M. Kondappan, V. Ivannikov, and T. Byrnes. “Two-axis two-spin squeezed states”. Phys. Rev. Research 2, 033504 (2020).
https://doi.org/10.1103/PhysRevResearch.2.033504

[37] C. Helstrom. “Minimum mean-squared error of estimates in quantum statistics”. Phys. Lett. A 25, 101–102 (1967).
https://doi.org/10.1016/0375-9601(67)90366-0

[38] S. L. Braunstein and C. M. Caves. “Statistical distance and the geometry of quantum states”. Phys. Rev. Lett. 72, 3439 (1994).
https://doi.org/10.1103/PhysRevLett.72.3439

[39] S. L. Braunstein, C. M. Caves, and G. J. Milburn. “Generalized uncertainty relations: Theory, examples, and Lorentz invariance”. Annals of Physics 247, 135–173 (1996).
https://doi.org/10.1006/aphy.1996.0040

[40] M. G. A. Paris. “Quantum estimation for quantum technology”. Int. J. Quantum Inf. 7, 125 (2009).
https://doi.org/10.1142/S0219749909004839

[41] J. M. E. Fraïsse. “New concepts in quantum-metrology: From coherent averaging to Hamiltonian extensions”. PhD thesis. University of Tübingen. (2017).

[42] J. Liu, H. Yuan, X.-M. Lu, and X. Wang. “Quantum Fisher information matrix and multiparameter estimation”. J. Phys. A Math. Theor. (2019).
https://doi.org/10.1088/1751-8121/ab5d4d

[43] O. Giraud, P. Braun, and D. Braun. “Quantifying quantumness and the quest for queens of quantum”. New J. Phys. 12, 063005 (2010).
https://doi.org/10.1088/1367-2630/12/6/063005

[44] C. W. Helstrom. “Quantum detection and estimation theory”. J. Stat. Phys. 1, 231–252 (1969).
https://doi.org/10.1007/bf01007479

[45] A. Holevo. “Probabilistic and statistical aspects of quantum theory”. Edizioni della Normale Pisa. (2011).
https://doi.org/10.1007/978-88-7642-378-9

[46] R. Demkowicz-Dobrzański, W. Górecki, and M. Guţă. “Multi-parameter estimation beyond Quantum Fisher Information”. J. Phys. A: Math. Theor. 53, 363001 (2020).
https://doi.org/10.1088/1751-8121/ab8ef3

[47] A. S. Holevo. “Statistical decision theory for quantum systems”. J. Multivar. Anal. 3, 337–394 (1973).
https://doi.org/10.1016/0047-259X(73)90028-6

[48] S. Ragy, M. Jarzyna, and R. Demkowicz-Dobrzański. “Compatibility in multiparameter quantum metrology”. Phys. Rev. A 94, 052108 (2016).
https://doi.org/10.1103/PhysRevA.94.052108

[49] F. Albarelli, J. F. Friel, and A. Datta. “Evaluating the Holevo Cramér-Rao bound for multiparameter quantum metrology”. Phys. Rev. Lett. 123, 200503 (2019).
https://doi.org/10.1103/PhysRevLett.123.200503

[50] M. Tsang, F. Albarelli, and A. Datta. “Quantum Semiparametric Estimation”. Phys. Rev. X 10, 031023 (2020).
https://doi.org/10.1103/PhysRevX.10.031023

[51] F. Waldner, D. R. Barberis, and H. Yamazaki. “Route to chaos by irregular periods: Simulations of parallel pumping in ferromagnets”. Phys. Rev. A 31, 420–431 (1985).
https://doi.org/10.1103/PhysRevA.31.420

[52] M. Kuś, R. Scharf, and F. Haake. “Symmetry versus degree of level repulsion for kicked quantum systems”. Z. Phys. B: Condens. Matter 66, 129–134 (1987).
https://doi.org/10.1007/bf01312770

[53] F. Haake and D. L. Shepelyansky. “The kicked rotator as a limit of the kicked top”. Europhys. Lett. 5, 671–676 (1988).
https://doi.org/10.1209/0295-5075/5/8/001

[54] P. A. Braun, P. Gerwinski, F. Haake, and H. Schomerus. “Semiclassics of rotation and torsion”. Z. Phys. B: Condens. Matter 100, 115–127 (1996).
https://doi.org/10.1007/s002570050101

[55] G. Müller-Rigat, A. K. Srivastava, S. Kurdziałek, G. Rajchel-Mieldzioć, M. Lewenstein, and I. Frérot. “Certifying the quantum fisher information from a given set of mean values: a semidefinite programming approach” (2023). url: arxiv.org/abs/2306.12711v2.
arXiv:2306.12711v2

[56] W. H. Zurek. “Sub-Planck structure in phase space and its relevance for quantum decoherence”. Nature (2001).
https://doi.org/10.1038/35089017

[57] M. Jarzyna and R. Demkowicz-Dobrzański. “Quantum interferometry with and without an external phase reference”. Phys. Rev. A 85, 011801 (2012).
https://doi.org/10.1103/PhysRevA.85.011801

[58] C. You, S. Adhikari, X. Ma, M. Sasaki, M. Takeoka, and J. P. Dowling. “Conclusive precision bounds for SU(1,1) interferometers”. Phys. Rev. A 99, 042122 (2019).
https://doi.org/10.1103/PhysRevA.99.042122

[59] Y. Aharonov and T. Kaufherr. “Quantum frames of reference”. Phys. Rev. D 30, 368–385 (1984).
https://doi.org/10.1103/PhysRevD.30.368

[60] S. D. Bartlett, T. Rudolph, and R. W. Spekkens. “Reference frames, superselection rules, and quantum information”. Rev. Mod. Phys. 79, 555 (2007).
https://doi.org/10.1103/RevModPhys.79.555

[61] F. Giacomini and C. Brukner. “Quantum superposition of spacetimes obeys Einstein’s equivalence principle”. AVS Quantum Science 4, 015601 (2022).
https://doi.org/10.1116/5.0070018

[62] D. Kajtoch and E. Witkowska. “Quantum dynamics generated by the two-axis countertwisting Hamiltonian”. Phys. Rev. A 92, 013623 (2015).
https://doi.org/10.1103/PhysRevA.92.013623

[63] T. Hernández Yanes, M. Płodzień, M. Mackoit Sinkevičienė, G. Žlabys, G. Juzeliūnas, and E. Witkowska. “One- and two-axis squeezing via laser coupling in an atomic Fermi-Hubbard model”. Phys. Rev. Lett. 129, 090403 (2022).
https://doi.org/10.1103/PhysRevLett.129.090403

[64] X.-M. Lu and X. Wang. “Incorporating Heisenberg’s uncertainty principle into quantum multiparameter estimation”. Phys. Rev. Lett. 126, 120503 (2021).
https://doi.org/10.1103/PhysRevLett.126.120503

[65] H. Ferretti, Y. B. Yilmaz, K. Bonsma-Fisher, A. Z. Goldberg, N. Lupu-Gladstein, A. O. T. Pang, L. A. Rozema, and A. M. Steinberg. “Generating a 4-photon tetrahedron state: Towards simultaneous super-sensitivity to non-commuting rotations” (2023). url: arxiv.org/abs/2310.17150v1.
arXiv:2310.17150v1

[66] A. S. Chirkin, A. A. Orlov, and D. Y. Parashchuk. “Quantum theory of two-mode interactions in optically anisotropic media with cubic nonlinearities: Generation of quadrature- and polarization-squeezed light”. Quantum Elec. 23, 870 (1993).
https://doi.org/10.1070/QE1993v023n10ABEH003182

[67] D. M. Klyshko. “Polarization of light: Fourth-order effects and polarization-squeezed states”. JETP 84, 1065–1079 (1997).
https://doi.org/10.1134/1.558243

[68] N. Korolkova, G. Leuchs, R. Loudon, T. C. Ralph, and C. Silberhorn. “Polarization squeezing and continuous-variable polarization entanglement”. Phys. Rev. A 65, 052306 (2002).
https://doi.org/10.1103/PhysRevA.65.052306

[69] R. Schnabel, W. P. Bowen, N. Treps, T. C. Ralph, H.-A. Bachor, and P. K. Lam. “Stokes-operator-squeezed continuous-variable polarization states”. Phys. Rev. A 67, 012316 (2003).
https://doi.org/10.1103/PhysRevA.67.012316

Cited by

[1] R. J. Lewis-Swan, J. C. Zuñiga Castro, D. Barberena, and A. M. Rey, “Exploiting Nonclassical Motion of a Trapped Ion Crystal for Quantum-Enhanced Metrology of Global and Differential Spin Rotations”, Physical Review Letters 132 16, 163601 (2024).

The above citations are from SAO/NASA ADS (last updated successfully 2024-05-08 14:59:17). The list may be incomplete as not all publishers provide suitable and complete citation data.

Could not fetch Crossref cited-by data during last attempt 2024-05-08 14:59:16: Could not fetch cited-by data for 10.22331/q-2024-05-08-1341 from Crossref. This is normal if the DOI was registered recently.

This Paper is published in Quantum under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. Copyright remains with the original copyright holders such as the authors or their institutions.

SEO Powered Content & PR Distribution. Get Amplified Today.
PlatoData.Network Vertical Generative Ai. Empower Yourself. Access Here.
PlatoAiStream. Web3 Intelligence. Knowledge Amplified. Access Here.
PlatoESG. Carbon, CleanTech, Energy, Environment, Solar, Waste Management. Access Here.
PlatoHealth. Biotech and Clinical Trials Intelligence. Access Here.
Source: https://quantum-journal.org/papers/q-2024-05-08-1341/

Time Stamp: May 8, 2024

Time Stamp: Feb 21, 2023

Qubit-efficient encoding schemes for binary optimisation problems

Source Cluster:

Quantum Journal

Source Node: 844778

Time Stamp: May 4, 2021

Transitions in Entanglement Complexity in Random Circuits

Source Cluster:

Quantum Journal

Source Node: 1678592

Time Stamp: Sep 22, 2022

Resource Marginal Problems

Source Cluster:

Quantum Journal

Source Node: 2581098

Time Stamp: May 22, 2024

Minimal-noise estimation of noncommuting rotations of a spin

Republished By Plato

Abstract

Popular summary

► BibTeX data

► References

Cited by

More from Quantum Journal

Classification of measurement-based quantum wire in stabilizer PEPS

Gravitational quantum switch on a superposition of spherical shells

Variational quantum algorithm for unconstrained black box binary optimization: Application to feature selection

Introduction to Haar Measure Tools in Quantum Information: A Beginner’s Tutorial

Impact of conditional modelling for a universal autoregressive quantum state

Classifying phases protected by matrix product operator symmetries using matrix product states

Qubit-efficient encoding schemes for binary optimisation problems

Transitions in Entanglement Complexity in Random Circuits

Resource Marginal Problems

About Us

Vertical Search & Ai

Platform

Stay Connected

Account