Cel mai mare cel mai mic triunghi tocmai a devenit mai mic | Revista Quanta

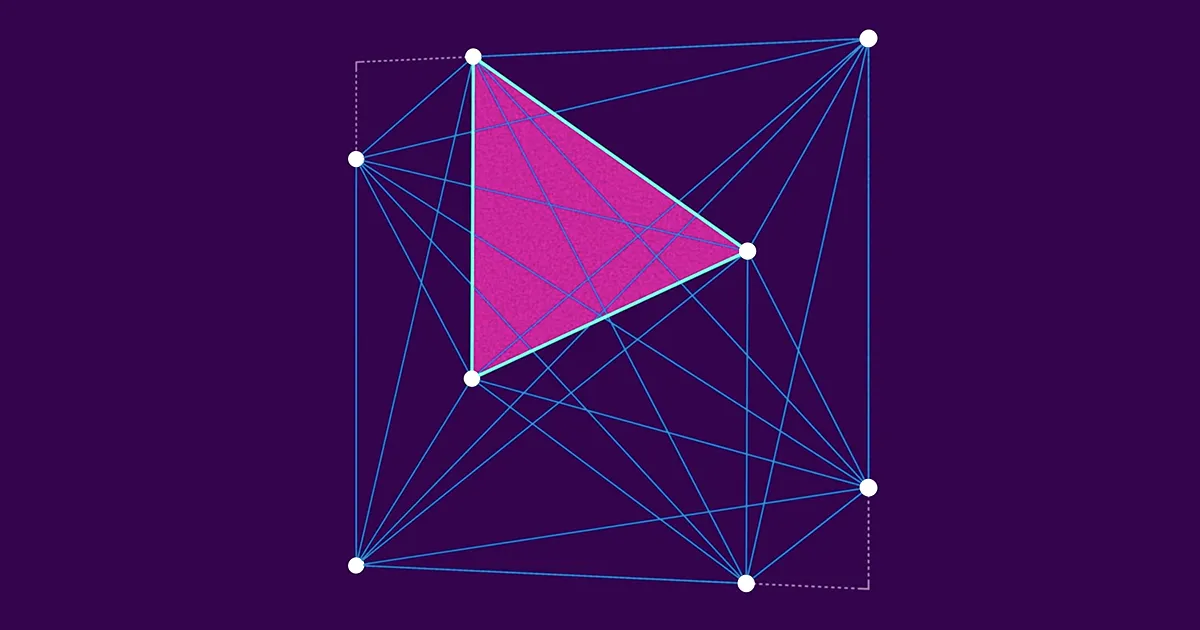
Luați în considerare un pătrat cu o grămadă de puncte înăuntru. Luați trei dintre aceste puncte și puteți face un triunghi. Patru puncte definesc patru triunghiuri diferite. Zece puncte definesc 120 de triunghiuri. Numerele cresc rapid de acolo - 100 de puncte definesc 161,700 de triunghiuri diferite. Fiecare dintre aceste triunghiuri, desigur, are o anumită zonă.

Hans Heilbronn, un matematician german care a fugit din țara sa înainte de al Doilea Război Mondial și s-a stabilit în Anglia, s-a gândit la aceste triunghiuri la sfârșitul anilor 1940 când a văzut un grup de soldați în fața ferestrei sale. Soldații nu păreau să fie în formație, ceea ce l-a făcut să se gândească: Dacă există n soldați în interiorul unui pătrat, care este dimensiunea celui mai mare și mai mic triunghi posibil definit de trei dintre ei? Heilbronn s-a întrebat cum s-ar putea proceda în aranjarea soldaților (sau, pentru simplitate matematică, a punctelor) pentru a maximiza dimensiunea celui mai mic triunghi.

Problema este simplu de afirmat, dar progresul în problema triunghiului Heilbronn, așa cum a ajuns să fie numit, a fost oprit, iar rezultatele s-au secat complet în anii 1980. Apoi, în luna mai trecută, trei matematicieni... Alex Cohen, Cosmin Pohoata și Dmitrii Zaharov — a anunțat a capac nou pe dimensiunea celui mai mic triunghi. „Cred că este un rezultat uimitor”, a spus Anthony Carbery, un matematician la Universitatea din Edinburgh.

Cercetătorii au continuat să lucreze la problema triunghiului Heilbronn de-a lungul anilor, în ciuda așteptării îndelungate pentru progres, motivat de încurcătura de legături cu alte domenii ale matematicii. „Lucrurile cu care este conectat pentru a-l face să prindă viață”, a spus Pohoata, profesor la Universitatea Emory din Atlanta. Este strâns legat de problemele legate de intersectarea formelor, care la rândul lor se conectează atât la teoria numerelor, cât și la analiza Fourier - studiul funcțiilor complicate construite din unde simple.

Cohen, un student absolvent la Institutul de Tehnologie din Massachusetts, a dat peste această rețea de conexiuni anul trecut. Citește un studiu vechi al problemei triunghiului Heilbronn de către Klaus Roth, un alt refugiat din rândul naziștilor care a fugit în Marea Britanie când era copil. (Roth, care a murit în 2015, a fost primul matematician britanic care a câștigat medalia Fields.)

Cohen a vizualizat ideile din sondajul lui Roth cu o imagine simplă: un pătrat încrucișat de două benzi groase, cu o linie subțire în mijlocul fiecăreia. În timp ce își studia diagrama, Cohen și-a dat seama că s-ar putea conecta la ideile pe care consilierul său, Larry Guth, le-a adus în discuție la o întâlnire recentă a grupului de lectură. Dar Guth nu vorbise deloc despre triunghiuri.

„Mi-am dat seama foarte repede că aceste două metode erau în esență echivalente”, a spus Cohen. „Am fost foarte entuziasmat de problema triunghiului.”

Într-o zi, în sala comună a departamentului de matematică al MIT, Cohen a descoperit pe neașteptate că Pohoata, care venise să țină o conferință, și Zakharov, un coleg absolvent la MIT, lucraseră și ei la problema triunghiului Heilbronn. Mai mult, găsiseră același link. Cei trei au început să colaboreze. Șapte luni mai târziu, ei și-au făcut progresul. Lucrarea lor aduce și mai multe domenii noi ale matematicii. „Ei folosesc o cantitate imensă de mașini și perspective diferite”, a spus Thomas Bloom de la Universitatea din Oxford, care a spus că se așteaptă ca noua lucrare să „promuleze o renaștere” a progresului în problema triunghiului.

O ipoteză a căzut

Prin plasarea a trei puncte foarte apropiate, puteți face cu ușurință cel mai mic triunghi dintr-un aranjament arbitrar mic. (În cel mai extrem caz, trei puncte în linie unul cu celălalt formează un triunghi cu zonă zero.) Dar încercarea de a menține cel mai mic triunghi mare este mai dificilă. Pe măsură ce continuați să adăugați mai multe puncte, cel mai mic triunghi este forțat să fie destul de mic - punctele noi pot fi doar atât de departe de cele existente. Este relativ ușor să arăți că cel mai mic triunghi nu poate avea o zonă mai mare de 1/(n − 2) prin împărțirea pătratului în triunghiuri care nu se suprapun.

Dar Heilbronn credea că limita era chiar mai mică decât atât. El a ghicit că, indiferent de modul în care erau aranjate punctele în pătrat, nu putea exista un triunghi cel mai mic cu o zonă mai mare de aproximativ 1/n², un număr care se micșorează mult mai repede ca n dezvoltă.

El a greșit.

În 1980, matematicienii maghiari János Komlós, János Pintz și Endre Szemerédi a găsit un model de puncte al căror triunghi cel mai mic avea o zonă puțin mai mare de 1/n². Într-o lucrare separată publicată în aceeași perioadă, ei au arătat, de asemenea, că este imposibil de aranjat n puncte pentru a crea cel mai mic triunghi care este mai mare decât aproximativ 1/n^8/7. Când n este mare, aceasta este mult mai mică decât 1/n, dar mult mai mare decât 1/n².

Aceste rezultate au durat peste 40 de ani. „Îmbunătățirea [legăturii] în ambele direcții a fost remarcabil de grea și a necesitat multă analiză tehnică și ingeniozitate”, a spus Bloom.

„Ești foarte, foarte repede blocat de o mlaștină completă de lucruri”, a adăugat Carbery.

În timp ce construcția descoperită în 1980 rămâne cea cu cel mai mare și mai mic triunghi cunoscut, Cohen, Pohoata și Zaharov au reușit, pentru prima dată în patru decenii, să coboare limita superioară.

Evoluție convergentă

Când l-a cunoscut pe Cohen, Pohoata lucra deja de doi ani la problema triunghiului Heilbronn. În vara anului 2020, el a pus studenți de cercetare de vară de la Universitatea Yale să lucreze la versiuni cu dimensiuni mai mari ale problemei - de exemplu, restrângerea celor mai mari forme de cel mai mic volum care apar printre punctele împrăștiate într-un cub tridimensional.

Ca parte a acestui proiect, Pohoata a reluat toate lucrările anterioare asupra problemei. Înapoi în 1951, Roth a împărțit căutarea triunghiurilor mici în două părți: mai întâi găsiți o pereche de puncte pentru a forma baza triunghiului și apoi găsiți un al treilea punct pentru a completa triunghiul. Strategia a încadrat în esență căutarea unui triunghi mare cel mai mic ca studiul punctelor și dreptunghiurilor care se intersectează - o abordare care a fost rafinată în 1972 de Wolfgang Schmidt.

Citind lucrarea lui Schmidt, Pohoata a identificat o conexiune cu metoda high-low - o tehnică pe care Guth și colaboratorii au dezvoltat-o ​​în 2017 pentru a estima suprapunerea dintre o colecție de benzi dreptunghiulare și o colecție de discuri. „Acesta a fost un moment psihologic important pentru mine”, a spus el.

În 2021, Pohoata și-a adus ideile cu Zakharov. Cei doi începuseră să publice împreună când Zaharov era încă student la Moscova. „[Zakharov] făcea lucruri remarcabile de parcă ar fi fost un cercetător senior la o vârstă fragedă”, a spus Jacob Fox, un matematician la Universitatea Stanford.

Zaharov a fost inițial pesimist cu privire la problema triunghiului Heilbronn. „M-am gândit că, ei bine, acest 8/7 a stat acolo sus timp de 40 de ani, deci cine sunt eu să-l sparg?” el a spus. „În mare parte, am vrut să înțeleg cum funcționează.”

După ce s-au întâlnit unul cu celălalt în octombrie 2022, Cohen, Pohoata și Zakharov au identificat în curând obstacolul cu care Komlós, Pintz și Szemerédi s-au confruntat fără să știe. „Există un aranjament foarte specific al punctelor care duce la acest scenariu cel mai rău caz în care nu pot face mai bine decât 8/7”, a spus Cohen. „Punctele pot fi fie concentrate, fie răspândite. Cel mai rău caz este atunci când este o combinație.” Acel aranjament avea puncte răspândite pe o scară mare, dar dacă ați mărit pe subpătrate mici din pătratul unității, veți vedea modele ordonate.

Cohen, Pohoata și Zakharov și-au dat seama că ar putea face progrese studiind dimensiunea micilor grupuri de puncte. Pentru non-matematicieni, dimensiunile sunt întotdeauna numere întregi: O coală de hârtie este bidimensională; o cărămidă de lut are trei dimensiuni.

Lucrurile pot deveni ciudate când luați în considerare dimensiunea unui set de puncte. Un singur punct este în mod normal considerat zero-dimensional. Dar două seturi finite de puncte pot avea structuri complet diferite. Unul ar putea avea 10 puncte care marșează ascultător într-o linie dreaptă, în timp ce celălalt are 10 puncte presărate pe întregul pătrat al unității.

Pentru a surprinde structura chiar și a celor mai ciudate seturi de puncte, matematicianul de la începutul secolului al XX-lea Felix Hausdorff a venit cu o nouă noțiune de dimensiune. Conform acestei definiții, 20 puncte dintr-o linie sunt unidimensionale, în timp ce 10 puncte distribuite uniform pe un pătrat sunt bidimensionale. Dar în această lume, dimensiunile nu trebuie să fie numere întregi, iar un set unidimensional poate fi nu liniar, ci fractal, prezentând straturi infinite de modele complicate. În funcție de detaliile acestor modele, colecțiile de puncte pot avea chiar și o dimensiune mai mare decât 10, dar mai mică de 0.

Cohen, Pohoata și Zaharov au descoperit a teorema 1953 de John Marstrand, care a reformulat estimarea lui Komlós, Pintz și Szemerédi în termeni de dimensiune Hausdorff — dar numai pentru dimensiuni mai mari de 1. Pentru a îmbunătăți estimarea, Cohen, Pohoata și Zakharov ar trebui să găsească o modalitate de a generaliza rezultatul lui Marstrand la seturi. a căror dimensiune era mai mică de 1.

A face legături

Cohen, Pohoata și Zakharov nu au fost nevoiți să se gândească mult. După cum sa întâmplat, o hârtie de Tuomas Orponen, Pablo Shmerkin și Hong Wang asta tocmai fusese postat on-line a extins teorema lui Marstrand de 70 de ani la mulțimi a căror dimensiune era mai mică de 1.

Cohen nu a aflat despre ziar decât în ​​februarie. Odată ce a făcut-o, le-a transmis rapid lui Pohoata și Zakharov. Până la sfârșitul lunii mai, își postaseră ziarul online, dovedind că cel mai mic triunghi dintre acestea n punctele dintr-un pătrat unitar nu pot fi niciodată mai mari de 1/n^{8 / 7 + 1 / 2000}.

Shmerkin a citit ziarul triunghi dintr-un capriciu, după ce a văzut-o anunțată pe Twitter. Nici măcar nu fusese conștient de problema triunghiului Heilbronn până atunci, așa că a fost surprins când a văzut referirea la dovada lui. „Aceasta nu este o aplicare directă a ceea ce facem. Există o mulțime de muncă perspicace, creativă și tehnică în ea”, a spus el. „Pentru mine, a fost un sentiment grozav.”

Bloom, de asemenea, a fost impresionat. „Aș fi putut să mă uit la acea hârtie mult timp și să nu mă gândesc niciodată, oh, asta se aplică problemei triunghiului.”

În timp ce noul rezultat îmbunătățește exponentul lui Komlós, Pintz și Szemerédi cu doar o mică parte, a reînviat problema triunghiului Heilbronn, care de mult timp lângă. „S-ar putea să arunci o privire la el și să spui, căscă, căscă, căscă, nu arată atât de diferit de ceea ce era cunoscut în 1982. Dar a trecut foarte mult timp din 1982”, a spus Carbery.

Prin încorporarea metodei înalt-jos și a lucrării lui Orponen, Shmerkin și Wang, Cohen, Pohoata și Zakharov au demascat un nou set de legături între problema triunghiului Heilbronn și restul matematicii. După cum a spus Bloom, problema triunghiului a fost considerată „o problemă foarte frumoasă, foarte grea, pe care nu știm ce să facem. Dar ei au spus că este legat de o mulțime de alte lucruri.”

Unii cred că răspunsul adevărat la problema triunghiului lui Heilbronn nu va fi cu mult mai mare decât estimarea sa inițială de 1/n². „Dacă pun puncte într-un mod structurat, eșuez; dacă pun puncte într-un mod aleatoriu, atunci nu reușesc. Nu poate fi prea structurat, nu poate fi prea aleatoriu, prin urmare probabil că nu există”, a spus Bloom. Dar Zaharov speră la un răspuns diferit. Intuițiile care susțin un răspuns de 1/n² sunt „oarecum plictisitoare”, a spus el. „Aș prefera foarte mult să fie așa n^3/2. "