Entanglement-assisted Quantum Reed-Muller Tensor Product Codes

Republished By Plato

Followers: 0

Priya J. Nadkarni¹, Praveen Jayakumar^1,2, Arpit Behera^1,3, and Shayan Srinivasa Garani¹

¹Department of Electronic Systems Engineering, Indian Institute of Science, Bengaluru, India, 560012
²Department of Chemistry, University of Toronto, Toronto, Canada, M5S 3H6
³Department of Complex Systems, Weizmann Institute of Science, Rehovot, Israel, 7610001

Find this paper interesting or want to discuss? Scite or leave a comment on SciRate.

Abstract

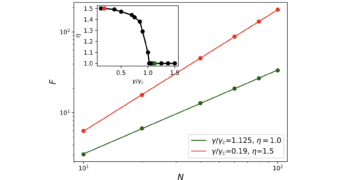
We present the construction of standard entanglement-assisted (EA) qubit Reed-Muller (RM) codes and their tensor product variants from classical RM codes. We show that the EA RM codes obtained using the CSS construction have zero coding rate and negative catalytic rate. We further show that EA codes constructed from these same classical RM codes using the tensor product code (TPC) construction have positive coding rate and provide a subclass of EA RM TPCs that have positive catalytic rate, thus establishing the coding analog of superadditivity for this family of codes, useful towards quantum communications. We also generalize this analysis to obtain conditions for EA TPCs from classical codes to have positive catalytic rate when their corresponding EA CSS codes have zero rate.

Featured image: Entanglement-assisted coding for quantum communications

Popular summary

The phenomenon of superadditivity of quantum channel capacity involving two zero-capacity quantum channels that achieve a positive quantum capacity does not have a classical bearing. A coding analog of this phenomenon was first demonstrated for quantum CSS codes. Two classical codes individually yielding zero-rate quantum codes were combined to obtain a positive rate quantum code using the quantum tensor product construction. The present study further demonstrates that the coding analog of superadditivity is applicable for constructing quantum codes from well-studied Reed-Muller codes that individually yield zero-rate quantum codes. Conditions for observing this phenomena with polar codes and other classical codes are provided. Our findings enable the construction of many algebraic quantum codes with good properties, useful towards quantum communications.

► BibTeX data

@article{Nadkarni2024entanglement, doi = {10.22331/q-2024-05-02-1329}, url = {https://doi.org/10.22331/q-2024-05-02-1329}, title = {Entanglement-assisted {Q}uantum {R}eed-{M}uller {T}ensor {P}roduct {C}odes}, author = {Nadkarni, Priya J. and Jayakumar, Praveen and Behera, Arpit and Garani, Shayan Srinivasa}, journal = {{Quantum}}, issn = {2521-327X}, publisher = {{Verein zur F{“{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}}, volume = {8}, pages = {1329}, month = may, year = {2024} }

► References

[1] P. W. Shor, “Scheme for reducing decoherence in quantum computer memory,” Phys. Rev. A, vol. 52, pp. 2493-2496, October 1995, doi: 10.1103/PhysRevA.52.R2493.
https://doi.org/10.1103/PhysRevA.52.R2493

[2] D. Gottesman, “Stabilizer codes and quantum error correction,” CalTech Ph.D Thesis, May 1997, doi: 10.48550/arXiv.quant-ph/9705052.
https://doi.org/10.48550/arXiv.quant-ph/9705052
arXiv:quant-ph/9705052

[3] A. R. Calderbank and P. W. Shor, “Good quantum error-correcting codes exist,” Physical Review A, vol. 54, no. 2, pp. 1098-1105, August 1996, doi: 10.1103/PhysRevA.54.1098.
https://doi.org/10.1103/PhysRevA.54.1098

[4] A. M. Steane, “Error correcting codes in quantum theory,” Physical Review Letters, vol. 77, no. 5, pp. 793-797, July 1996, doi: 10.1103/PhysRevLett.77.793.
https://doi.org/10.1103/PhysRevLett.77.793

[5] T. Brun, I. Devetak and M.-H. Hsieh, “Correcting quantum errors with entanglement,” Science, vol. 314, no. 5798, pp. 436-439, October 2006, doi: 10.1126/science.1131563.
https://doi.org/10.1126/science.1131563

[6] Min-Hsiu Hsieh, Igor Devetak, and Todd Brun, “General entanglement-assisted quantum error-correcting codes,” Physical Review A, vol. 76, no. 6, p. 062313, December 2007, doi: 10.1103/PhysRevA.76.062313.
https://doi.org/10.1103/PhysRevA.76.062313

[7] K. Guenda, S. Jitman, and T. A. Gulliver, “Constructions of good entanglement-assisted quantum error correcting codes,” Designs, Codes and Cryptography, vol. 86, no. 1, pp. 121-136, January 2017, doi: 10.1007/s10623-017-0330-z.
https://doi.org/10.1007/s10623-017-0330-z

[8] J. H. Bae, A. Abotabl, H.-P. Lin, K.-B. Song, and J. Lee, “An overview of channel coding for 5G NR cellular communications,” APSIPA Transactions on Signal and Information Processing, vol. 8, p. e17, June 2019, doi: 10.1017/ATSIP.2019.10.
https://doi.org/10.1017/ATSIP.2019.10

[9] I. Reed, “A class of multiple-error-correcting codes and the decoding scheme,” in Transactions of the IRE Professional Group on Information Theory, vol. 4, no. 4, pp. 38-49, September 1954, doi: 10.1109/TIT.1954.1057465.
https://doi.org/10.1109/TIT.1954.1057465

[10] R. Pellikaan and Xin-Wen Wu, “List decoding of q-ary Reed-Muller codes,” in IEEE Transactions on Information Theory, vol. 50, no. 4, pp. 679-682, April 2004, doi: 10.1109/TIT.2004.825043.
https://doi.org/10.1109/TIT.2004.825043

[11] G. Schnabl and M. Bossert, “Soft-decision decoding of Reed-Muller codes as generalized multiple concatenated codes,” in IEEE Transactions on Information Theory, vol. 41, no. 1, pp. 304-308, January 1995, doi: 10.1109/18.370093.
https://doi.org/10.1109/18.370093

[12] S. Kudekar, S. Kumar, M. Mondelli, H. D. Pfister, E. Şaşoǧlu and R. L. Urbanke, “Reed–Muller Codes Achieve Capacity on Erasure Channels,” in IEEE Transactions on Information Theory, vol. 63, no. 7, pp. 4298-4316, July 2017, doi: 10.1109/TIT.2017.2673829.
https://doi.org/10.1109/TIT.2017.2673829

[13] S. Kumar, R. Calderbank and H. D. Pfister, “Reed-muller codes achieve capacity on the quantum erasure channel,” International Symposium on Information Theory, Barcelona, Spain, pp. 1750-1754, July 2016, doi: 10.1109/ISIT.2016.7541599.
https://doi.org/10.1109/ISIT.2016.7541599

[14] A. M. Steane, “Quantum Reed-Muller codes,” in IEEE Transactions on Information Theory, vol. 45, no. 5, pp. 1701-1703, July 1999, doi: 10.1109/18.771249.
https://doi.org/10.1109/18.771249

[15] P. K. Sarvepalli and A. Klappenecker, “Nonbinary quantum Reed-Muller codes,” in Proceedings. International Symposium on Information Theory, Adelaide, SA, Australia, pp. 1023-1027, September 2005, doi: 10.1109/ISIT.2005.1523494.
https://doi.org/10.1109/ISIT.2005.1523494

[16] J. K. Wolf, “An introduction to tensor product codes and applications to digital storage systems,” in 2006 IEEE Information Theory Workshop, Chengdu, pp. 6-10, October 2006, doi: 10.1109/ITW2.2006.323741.
https://doi.org/10.1109/ITW2.2006.323741

[17] S. Bravyi and A. Kitaev, “Universal quantum computation with ideal Clifford gates and noisy ancillas,” Phys. Rev. A, vol. 71, no. 2, p. 022316, February 2005, doi: 10.1103/PhysRevA.71.022316.
https://doi.org/10.1103/PhysRevA.71.022316

[18] N. Rengaswamy, R. Calderbank, M. Newman and H. D. Pfister, “Classical coding problem from transversal T gates,” International Symposium on Information Theory, Los Angeles, CA, USA, June 2020, pp. 1891-1896, doi: 10.1109/ISIT44484.2020.9174408.
https://doi.org/10.1109/ISIT44484.2020.9174408

[19] P. J. Nadkarni and S. S. Garani, “Coding analog of superadditivity using entanglement-assisted quantum tensor product codes over $mathbb {F}_{p^k}$,” in IEEE Transactions on Quantum Engineering, vol. 1, pp. 1-17, Art no. 2101417, September 2020, doi: 10.1109/TQE.2020.3027035.
https://doi.org/10.1109/TQE.2020.3027035

[20] P. J. Nadkarni and S. S. Garani, “Optimal interleavers for classical and quantum tensor product codes,” in IEEE Communications Letters, vol. 25, no. 11, pp. 3478-3482, November 2021, doi: 10.1109/LCOMM.2021.3110236.
https://doi.org/10.1109/LCOMM.2021.3110236

[21] E. Abbe, A. Shpilka and M. Ye, “Reed–Muller codes: Theory and algorithms,” in IEEE Transactions on Information Theory, vol. 67, no. 6, pp. 3251-3277, June 2021, doi: 10.1109/TIT.2020.3004749.
https://doi.org/10.1109/TIT.2020.3004749

[22] F. J. MacWilliams and N. J. Sloane, “The theory of error-correcting codes,” Elsevier Science, 1978, ISBN: 9780444851932.

[23] M. M. Wilde, “Quantum coding with entanglement”, PhD dissertation, Univ. of South. Cal., August 2008, doi: 10.48550/arXiv.0806.4214.
https://doi.org/10.48550/arXiv.0806.4214

[24] P. J. Nadkarni and S. S. Garani, “Non-binary entanglement-assisted stabilizer codes,” Quantum Inf Process, vol. 20, article no. 256, August 2021, doi: 10.1007/s11128-021-03174-1.
https://doi.org/10.1007/s11128-021-03174-1

[25] J. Wolf, “On codes derivable from the tensor product of check matrices,” IEEE Transactions on Information Theory, vol. 11, no. 2, pp. 281-284, April 1965, doi: 10.1109/TIT.1965.1053771.
https://doi.org/10.1109/TIT.1965.1053771

[26] P. J. Nadkarni and S. S. Garani, “Entanglement assisted binary quantum tensor product codes,” in Proc. IEEE Inf. Theory Workshop, Kaohsiung, pp. 219–223, November 2017, doi: 10.1109/ITW.2017.8277961.
https://doi.org/10.1109/ITW.2017.8277961

[27] J. Fan, Y. Li, M.-H. Hsieh, and H. Chen, “On quantum tensor product codes,” Quantum Info. Comput., vol. 17, no. 13&14, p. 1105-1122, November 2017, doi: 10.48550/arXiv.1605.09598.
https://doi.org/10.48550/arXiv.1605.09598

[28] J. Fan, J. Li, J. Wang, Z. Wei, and M. -H. Hsieh, “Asymmetric Quantum Concatenated and Tensor Product Codes With Large Z-Distances,” IEEE Trans. Comm., vol. 69, no. 6, pp. 3971-3983, June 2021, doi: 10.1109/TCOMM.2021.3064566.
https://doi.org/10.1109/TCOMM.2021.3064566

[29] P. Rózsa, “Applied dimensional analysis and modeling” 2nd Ed., Butterworth-Heinemann, 2007, ISBN 978-0-12-370620-1. doi: 10.1016/B978-012370620-1.50007-1.
https://doi.org/10.1016/B978-012370620-1.50007-1

[30] M. Grassl, F. Huber, and A. Winter, “Entropic proofs of Singleton bounds for quantum error-correcting codes,” in IEEE Transactions on Information Theory, vol. 68, no. 6, pp. 3942-3950, June 2022, doi: 10.1109/TIT.2022.3149291.
https://doi.org/10.1109/TIT.2022.3149291

[31] P. J. Nadkarni and S. S. Garani, “Entanglement assisted quantum Reed-Solomon codes,” Information Theory and Applications Workshop 2019, San Diego, February 2019.

[32] P. J. Nadkarni and S. S. Garani, “Entanglement-assisted Reed–Solomon codes over qudits: Theory and architecture,” Quantum Inf. Process., vol. 20, Art no. 129, April 2021, doi: 10.1007/s11128-021-03028-w.
https://doi.org/10.1007/s11128-021-03028-w

[33] P. J. Nadkarni and S. S. Garani, “$mathbb {F}_p$-Linear and $mathbb{F}_{p^m}$-Linear Qudit Codes From Dual-Containing Classical Codes,” in IEEE Transactions on Quantum Engineering, vol. 2, pp. 1-19, Art no. 2101819, May 2021, doi: 10.1109/TQE.2021.3078152.
https://doi.org/10.1109/TQE.2021.3078152

Cited by

This Paper is published in Quantum under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. Copyright remains with the original copyright holders such as the authors or their institutions.

SEO Powered Content & PR Distribution. Get Amplified Today.
PlatoData.Network Vertical Generative Ai. Empower Yourself. Access Here.
PlatoAiStream. Web3 Intelligence. Knowledge Amplified. Access Here.
PlatoESG. Carbon, CleanTech, Energy, Environment, Solar, Waste Management. Access Here.
PlatoHealth. Biotech and Clinical Trials Intelligence. Access Here.
Source: https://quantum-journal.org/papers/q-2024-05-02-1329/

Time Stamp: May 2, 2024

Time Stamp: Jan 4, 2024

Entanglement-assisted Quantum Reed-Muller Tensor Product Codes

Republished By Plato

Abstract

Popular summary

► BibTeX data

► References

Cited by

More from Quantum Journal

Metrology and multipartite entanglement in measurement-induced phase transition

Identifying families of multipartite states with non-trivial local entanglement transformations

Geometry of Degeneracy in Potential and Density Space

Quantum Proofs of Proximity

A relativistic discrete spacetime formulation of 3+1 QED

A Pair Measurement Surface Code on Pentagons

On low-depth algorithms for quantum phase estimation

Quantum-optimal information encoding using noisy passive linear optics

About Us

Vertical Search & Ai

Platform

Stay Connected

Account