Variational Quantum Solutions To The Shortest Vector Problem

Republished By Plato

Followers: 0

Martin R. Albrecht¹, Miloš Prokop², Yixin Shen³, and Petros Wallden⁴

¹King’s College London and SandboxAQ. email: martin.albrecht@kcl.ac.uk
²University of Edinburgh. email: m.prokop@sms.ed.ac.uk
³Royal Holloway, University of London. email: yixin.shen@rhul.ac.uk
⁴University of Edinburgh. email: petros.wallden@ed.ac.uk

Find this paper interesting or want to discuss? Scite or leave a comment on SciRate.

Abstract

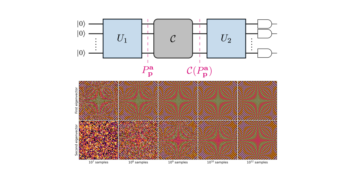
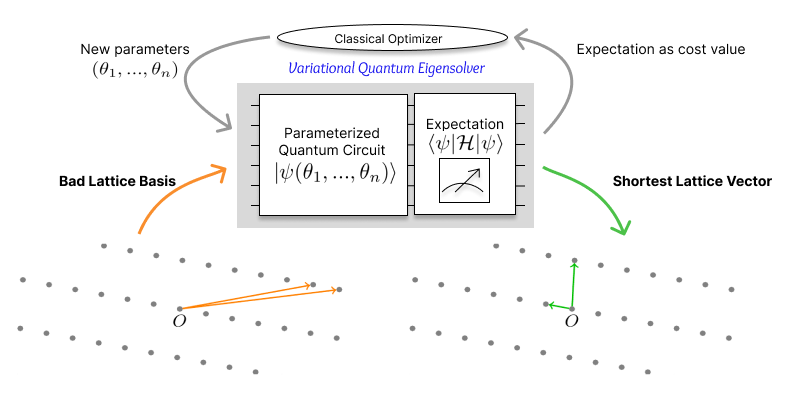
A fundamental computational problem is to find a shortest non-zero vector in Euclidean lattices, a problem known as the Shortest Vector Problem (SVP). This problem is believed to be hard even on quantum computers and thus plays a pivotal role in post-quantum cryptography. In this work we explore how (efficiently) Noisy Intermediate Scale Quantum (NISQ) devices may be used to solve SVP. Specifically, we map the problem to that of finding the ground state of a suitable Hamiltonian. In particular, (i) we establish new bounds for lattice enumeration, this allows us to obtain new bounds (resp. estimates) for the number of qubits required per dimension for any lattices (resp. random q-ary lattices) to solve SVP; (ii) we exclude the zero vector from the optimization space by proposing (a) a different classical optimisation loop or alternatively (b) a new mapping to the Hamiltonian. These improvements allow us to solve SVP in dimension up to 28 in a quantum emulation, significantly more than what was previously achieved, even for special cases. Finally, we extrapolate the size of NISQ devices that is required to be able to solve instances of lattices that are hard even for the best classical algorithms and find that with approximately $10^3$ noisy qubits such instances can be tackled.

Popular summary

Quantum computers potentially offer speed-ups in solving many problems. Existing encryption schemes, used in everyday life, are based on the assumption that factoring a large number is hard. However, a quantum algorithm due to Shor, can solve this problem using a large fault-tolerant quantum computer efficiently. This would compromise the security of all these communications. Because of this threat, alternative encryption schemes are being considered, where their security relies on assumptions about the hardness of other mathematical problems that are believed to be hard for quantum computers. The most prominent such problem is the Shortest-Vector-Problem (SVP). While SVP is strongly believed to be hard for quantum computers, it is not clear how hard it is, or else, what is the best that a quantum computer (fault-tolerant or not) can do in solving this problem.

In our work we examine how to solve the SVP using quantum computers and algorithms that can be run on exiting or near-term, imperfect, devices. We significantly reduce the number of qubits required to run such algorithms by providing bounds on the coefficients of the shortest-vector and by excluding the zero vector in a more efficient way. We are able to solve SVP for dimension 28 in a simulation, and we extrapolate that the classical record for SVP can be tackled using quantum computers with around one thousand qubits. We note, however, that our results do not invalidate any security claims made by post-quantum candidates as part of current standardisation efforts to replace cryptographic algorithms.

► BibTeX data

@article{Albrecht2023variationalquantum, doi = {10.22331/q-2023-03-02-933}, url = {https://doi.org/10.22331/q-2023-03-02-933}, title = {Variational quantum solutions to the {S}hortest {V}ector {P}roblem}, author = {Albrecht, Martin R. and Prokop, Milo{v{s}} and Shen, Yixin and Wallden, Petros}, journal = {{Quantum}}, issn = {2521-327X}, publisher = {{Verein zur F{“{o}}rderung des Open Access Publizierens in den Quantenwissenschaften}}, volume = {7}, pages = {933}, month = mar, year = {2023}<br /> }

► References

[1] Whitfield Diffie and Martin E. Hellman. “New directions in cryptography”. IEEE Transactions on Information Theory 22, 644–654 (1976).
https://doi.org/10.1109/TIT.1976.1055638

[2] Peter W. Shor. “Polynomial-time algorithms for prime factorization and discrete logarithms on a quantum computer”. SIAM J. Comput. 26, 1484–1509 (1997).
https://doi.org/10.1137/S0097539795293172

[3] NIST. “Post-quantum cryptography standardization”. Available at https://csrc.nist.gov/projects/post-quantum-cryptography/post-quantum-cryptography-standardization.
https://csrc.nist.gov/projects/post-quantum-cryptography/post-quantum-cryptography-standardization

[4] Léo Ducas, Marc Stevens, and Wessel P. J. van Woerden. “Advanced lattice sieving on GPUs, with tensor cores”. In Anne Canteaut and François-Xavier Standaert, editors, EUROCRYPT 2021, Part II. Volume 12697 of LNCS, pages 249–279. Springer, Heidelberg (2021).
https://doi.org/10.1007/978-3-030-77886-6_9

[5] Oded Regev. “On lattices, learning with errors, random linear codes, and cryptography”. In Harold N. Gabow and Ronald Fagin, editors, 37th ACM STOC. Pages 84–93. ACM Press (2005).
https://doi.org/10.1145/1060590.1060603

[6] A.K. Lenstra, H.W. Lenstra, and Lászlo Lovász. “Factoring polynomials with rational coefficients”. Math. Ann. 261, 515–534 (1982).
https://doi.org/10.1007/BF01457454

[7] Claus Peter Schnorr. “A hierarchy of polynomial time lattice basis reduction algorithms”. Theor. Comput. Sci. 53, 201–224 (1987).
https://doi.org/10.5555/2796561.2796598

[8] Martin R. Albrecht, Benjamin R. Curtis, Amit Deo, Alex Davidson, Rachel Player, Eamonn W. Postlethwaite, Fernando Virdia, and Thomas Wunderer. “Estimate all the LWE, NTRU schemes!”. In Dario Catalano and Roberto De Prisco, editors, Security and Cryptography for Networks – 11th International Conference, SCN 2018, Amalfi, Italy, September 5-7, 2018, Proceedings. Volume 11035 of Lecture Notes in Computer Science, pages 351–367. Springer (2018).
https://doi.org/10.1007/978-3-319-98113-0_19

[9] Ravi Kannan. “Improved algorithms for integer programming and related lattice problems”. In Proceedings of the Fifteenth Annual ACM Symposium on Theory of Computing. Page 193–206. STOC ’83New York, NY, USA (1983). Association for Computing Machinery.
https://doi.org/10.1145/800061.808749

[10] Guillaume Hanrot and Damien Stehlé. “Improved analysis of kannan’s shortest lattice vector algorithm”. In Alfred Menezes, editor, Advances in Cryptology – CRYPTO 2007. Pages 170–186. Berlin, Heidelberg (2007). Springer Berlin Heidelberg.
https://doi.org/10.1007/978-3-540-74143-5_10

[11] André Chailloux and Johanna Loyer. “Lattice sieving via quantum random walks”. In Mehdi Tibouchi and Huaxiong Wang, editors, Lattice Sieving via Quantum Random Walks. Pages 63–91. Cham (2021). Springer International Publishing.
https://doi.org/10.1007/978-3-030-92068-5_3

[12] Vittorio Giovannetti, Seth Lloyd, and Lorenzo Maccone. “Quantum random access memory”. Phys. Rev. Lett. 100, 160501 (2008).
https://doi.org/10.1103/PhysRevLett.100.160501

[13] Yoshinori Aono, Phong Q. Nguyen, and Yixin Shen. “Quantum lattice enumeration and tweaking discrete pruning”. In Thomas Peyrin and Steven Galbraith, editors, ASIACRYPT 2018, Part I. Volume 11272 of LNCS, pages 405–434. Springer, Heidelberg (2018).
https://doi.org/10.1007/978-3-030-03326-2_14

[14] Martin R. Albrecht, Shi Bai, Pierre-Alain Fouque, Paul Kirchner, Damien Stehlé, and Weiqiang Wen. “Faster enumeration-based lattice reduction: Root hermite factor $k^{1/(2k)}$ time $k^{k/8+o(k)}$”. In Daniele Micciancio and Thomas Ristenpart, editors, CRYPTO 2020, Part II. Volume 12171 of LNCS, pages 186–212. Springer, Heidelberg (2020).
https://doi.org/10.1007/978-3-030-56880-1_7

[15] M. Cerezo, Andrew Arrasmith, Ryan Babbush, Simon C. Benjamin, Suguru Endo, Keisuke Fujii, Jarrod R. McClean, Kosuke Mitarai, Xiao Yuan, Lukasz Cincio, and Patrick J. Coles. “Variational quantum algorithms”. Nature Reviews Physics (2021).
https://doi.org/10.1038/s42254-021-00348-9

[16] Ian Kivlichan, Jarrod Mcclean, Nathan Wiebe, Craig Gidney, AlÃ¡n Aspuru-Guzik, Garnet Chan, and Ryan Babbush. “Quantum simulation of electronic structure with linear depth and connectivity”. Physical review letters 120 (2017).
https://doi.org/10.1103/PhysRevLett.120.110501

[17] Roeland Wiersema, Cunlu Zhou, Yvette de Sereville, Juan Felipe Carrasquilla, Yong Baek Kim, and Henry Yuen. “Exploring entanglement and optimization within the hamiltonian variational ansatz”. PRX Quantum 1, 020319 (2020).
https://doi.org/10.1103/PRXQuantum.1.020319

[18] Andrew Lucas. “Ising formulations of many np problems”. Frontiers in Physics 2, 5 (2014).
https://doi.org/10.3389/fphy.2014.00005

[19] Alba Cervera-Lierta, Jakob S. Kottmann, and Alán Aspuru-Guzik. “Meta-variational quantum eigensolver: Learning energy profiles of parameterized hamiltonians for quantum simulation”. PRX Quantum 2, 020329 (2021).
https://doi.org/10.1103/PRXQuantum.2.020329

[20] B Koczor, S Endo, T Jones, Y Matsuzaki, and SC Benjamin. “Variational-state quantum metrology”. New Journal of Physics 22 (2020).
https://doi.org/10.1088/1367-2630/ab965e

[21] Alberto Peruzzo, Jarrod McClean, Peter Shadbolt, Man-Hong Yung, Xiao-Qi Zhou, Peter J. Love, Alán Aspuru-Guzik, and Jeremy L. O’Brien. “A variational eigenvalue solver on a photonic quantum processor”. Nature Communications 5 (2014).
https://doi.org/10.1038/ncomms5213

[22] Jarrod R McClean, Jonathan Romero, Ryan Babbush, and Alán Aspuru-Guzik. “The theory of variational hybrid quantum-classical algorithms”. New Journal of Physics 18, 023023 (2016).
https://doi.org/10.1088/1367-2630/18/2/023023

[23] Edward Farhi, Jeffrey Goldstone, Sam Gutmann, and Leo Zhou. “The Quantum Approximate Optimization Algorithm and the Sherrington-Kirkpatrick Model at Infinite Size”. Quantum 6, 759 (2022).
https://doi.org/10.22331/q-2022-07-07-759

[24] Philipp Hauke, Helmut G Katzgraber, Wolfgang Lechner, Hidetoshi Nishimori, and William D Oliver. “Perspectives of quantum annealing: methods and implementations”. Reports on Progress in Physics 83, 054401 (2020).
https://doi.org/10.1088/1361-6633/ab85b8

[25] Panagiotis Kl. Barkoutsos, Giacomo Nannicini, Anton Robert, Ivano Tavernelli, and Stefan Woerner. “Improving variational quantum optimization using cvar”. Quantum 4, 256 (2020).
https://doi.org/10.22331/q-2020-04-20-256

[26] Ioannis Kolotouros and Petros Wallden. “Evolving objective function for improved variational quantum optimization”. Phys. Rev. Res. 4, 023225 (2022).
https://doi.org/10.1103/PhysRevResearch.4.023225

[27] Sami Boulebnane and Ashley Montanaro. “Solving boolean satisfiability problems with the quantum approximate optimization algorithm” (2022). https://doi.org/10.48550/arXiv.2208.06909.
https://doi.org/10.48550/arXiv.2208.06909

[28] Edward Farhi, Jeffrey Goldstone, and Sam Gutmann. “A quantum approximate optimization algorithm applied to a bounded occurrence constraint problem” (2014). arXiv:1412.6062. https://doi.org/10.48550/arXiv.1412.6062.
https://doi.org/10.48550/arXiv.1412.6062
arXiv:1412.6062

[29] David Joseph, Alexandros Ghionis, Cong Ling, and Florian Mintert. “Not-so-adiabatic quantum computation for the shortest vector problem”. Phys. Rev. Research 2, 013361 (2020).
https://doi.org/10.1103/PhysRevResearch.2.013361

[30] David Joseph, Adam Callison, Cong Ling, and Florian Mintert. “Two quantum ising algorithms for the shortest-vector problem”. Phys. Rev. A 103, 032433 (2021).
https://doi.org/10.1103/PhysRevA.103.032433

[31] Gérard Maze. “Natural density distribution of hermite normal forms of integer matrices”. Journal of Number Theory 131, 2398–2408 (2010).
https://doi.org/10.1016/j.jnt.2011.06.010

[32] Oscar Higgott, Daochen Wang, and Stephen Brierley. “Variational Quantum Computation of Excited States”. Quantum 3, 156 (2019).
https://doi.org/10.22331/q-2019-07-01-156

[33] Yifeng Rocky Zhu, David Joseph, Cong Ling, and Florian Mintert. “Iterative quantum optimization with an adaptive problem hamiltonian for the shortest vector problem”. Phys. Rev. A 106, 022435 (2022).
https://doi.org/10.1103/PhysRevA.106.022435

[34] Martin R. Albrecht, Shi Bai, Jianwei Li, and Joe Rowell. “Lattice reduction with approximate enumeration oracles – practical algorithms and concrete performance”. In Tal Malkin and Chris Peikert, editors, CRYPTO 2021, Part II. Volume 12826 of LNCS, pages 732–759. Virtual Event (2021). Springer, Heidelberg.
https://doi.org/10.1007/978-3-030-84245-1_25

[35] Jinming Wen and Xiao-Wen Chang. “On the KZ reduction”. IEEE Trans. Inf. Theory 65, 1921–1935 (2019).
https://doi.org/10.1109/TIT.2018.2868945

[36] “Svp challenge”. https://www.latticechallenge.org/svp-challenge/.
https://www.latticechallenge.org/svp-challenge/

[37] Phong Q. Nguyen and Brigitte Vallée, editors. “The LLL algorithm – survey and applications”. ISC. Springer, Heidelberg. (2010).
https://doi.org/10.1007/978-3-642-02295-1

[38] Miklós Ajtai. “Generating hard instances of lattice problems (extended abstract)”. In 28th ACM STOC. Pages 99–108. ACM Press (1996).
https://doi.org/10.1145/237814.237838

[39] Alexander J McCaskey, Dmitry I Lyakh, Eugene F Dumitrescu, Sarah S Powers, and Travis S Humble. “XACC: a system-level software infrastructure for heterogeneous quantum–classical computing”. Quantum Science and Technology 5, 024002 (2020).
https://doi.org/10.1088/2058-9565/ab6bf6

[40] Tyson Jones, Anna Brown, Ian Bush, and Simon C. Benjamin. “Quest and high performance simulation of quantum computers”. Scientific Reports 9 (2019).
https://doi.org/10.1038/s41598-019-47174-9

[41] Herbert Robbins. “A remark on stirling’s formula”. The American Mathematical Monthly 62, 26–29 (1955).
https://doi.org/10.2307/2308012

Cited by

[1] Yifeng Rocky Zhu, David Joseph, Cong Ling, and Florian Mintert, “Iterative Quantum Optimization with Adaptive Problem Hamiltonian”, arXiv:2204.13432, (2022).

The above citations are from SAO/NASA ADS (last updated successfully 2023-03-03 15:54:53). The list may be incomplete as not all publishers provide suitable and complete citation data.

On Crossref’s cited-by service no data on citing works was found (last attempt 2023-03-03 15:54:52).

This Paper is published in Quantum under the Creative Commons Attribution 4.0 International (CC BY 4.0) license. Copyright remains with the original copyright holders such as the authors or their institutions.